6762

40

Приведем левую часть к общему знаменателю и перекрёстно перемножим

2

x = ±π + 2πk, x = π + 2πk, k Z. 3

Ответ. x = ±π + 2πk, x = π + 2πk, k Z.

3

Уравнения типа sin αx = sin βx , cosαx = cos βx , sinαx = cos βx , α , β R,

α, β ≠ 0 для последнего: α ≠ ±β решаются с помощью формул преобразования суммы в произведение, последнее ещё и с помощью формулы приведения.

Задача 15. Решить уравнение sin7x = sin3x .

Решение. По формуле (2.6) разность синусов преобразуем исходное уравнение

sin7x = sin3x sin7x − sin3x = 0 sin2xcos5x = 0.

Решения уравнений sin2x = 0 и cos5x = 0, соответственно, x = πk ,

2

x = π + πk , k Z. 10 5

запишем уравнение в виде

С помощью формулы (2.6) для суммы косинусов преобразуем исходное уравнение

x = 3π + πk, x = 3π + πk , k Z.

416 4

Ответ. x = 3π + πk, x = 3π + πk , k Z.

416 4

Задача 17. Решить уравнение sin3x + sin7x = 3cos2x.

Решение. С помощью формулы (2.6.) для суммы синусов преобразуем исходное уравнение

2sin5x cos2x = 3cos2x 2sin5x cos2x − 3cos2x = 0

Ответ.x = π + πk , k Z.

42

Задача 18. Решить уравнение cos3x cosx = cos2x.

Решение. С помощью формулы (2.2.) для синуса разности преобразуем исходное уравнение

42

cos3x cosx = (cos3x − x) cos3x cosx = cos3x cosx + sin3x sin x

sin3x sinx = 0.

Корни уравнений sin3x = 0 и sin x = 0 соответственно x = πk ,

3

x = πk, k Z. Корни второго уравнения содержатся в серии корней первого, так

как, если k = 3n, то πk = πn. 3

Ответ.x = πk , k Z. 3

1) tgx +1= 0, tgx = −1, x = −π + πk , k Z. 4

Эти значения x являются корнями исходного уравнения, так как при этом

первая скобка левой части уравнения равна нулю, а вторая не теряет смысла.

При этих значениях x вторая скобка левой части исходного уравнения равна нулю, а первая скобка не имеет смысла. Поэтому эти значения не являются корнями исходного уравнения.

Ответ. x = −π + πk , k Z.

4

Задача 20. Решить уравнение 6sin2 x + 2sin2 2x = 5.

Решение. Используя формулу 2.3 для косинуса двойного аргумента и основное тригонометрическое тождество, преобразуем исходное уравнение

3(1− cos2x)+ 2(1− cos2 2x)= 5 или

2cos2 2x + 3cos2x = 0, cos2x(2cos2x + 3)= 0.

43

1) cos2x = 0, x = π + πk , k Z.

42

2)уравнение cos2x = − 3 корней не имеет.

2

4. Решить уравнения

4.1. 1+ 7cos2 x = 3sin2x ; 4.2. 4.3. 3 + sin2x = 4sin2 x ;

4.3.сos2x + cos2 x + sin xcosx = 0;

4.4.3сos2x + sin2 x + 5sin xcosx = 0.

12. Решить уравнения

12.1.2sin2x − 3(sin x + cosx)+ 2 = 0;

12.2.sin2x + 3 = 3sinx + 3cosx ;

12.3.sin2x + 4(sin x + cosx)+ 4 = 0;

12.4.sin2x + 5(cosx − sin x +1)= 0.

13. Решить уравнения

15. Решить уравнения

15.1.2cos2 2x + 3sin4x + 4sin2 2x = 0;

15.2.1− sin xcosx + 2cos2 x = 0;

15.3.2sin2 x + 1 cos3 2x =1;

4

15.4. sin2 2x + cos2 3x =1+ 4sinx .

x = ± 2π + 2πk , k Z. 3.1. x = ±arctg2 + πn , n Z; 3.2. x = π + πk , k Z; 3.3.

x = π + πn , n Z; 3.6. корней нет 4.1. x = arctg2 + πn, x = arctg4 + πn, n Z. 4.2.

x = π + πk, x = −π + πk, k Z. 10.1. x = π + πk, x =πk, k Z; 10.2. x = π + πk,

x = πk; 16.4. x = πk , k Z. 5

48

6.Решение простейших тригонометрических неравенств

Втригонометрических неравенствах аргументы тригонометрических функций рассматриваются как действительные числа.

К простейшим тригонометрическим неравенствам относятся неравенства

Задача 1. Решить неравенство cosx > 1. 2

Решение. Косинус угла x равен абсциссе точки единичной окружности.

Чтобы решить неравенство cosx > 1 , нужно выяснить, какие точки единичной 2

окружности имеют абсциссу, большую 1. 2

Абсциссу, равную 1 , имеют две точки единичной окружности M1 и M2 2

углы, π + 2πn где n = ±1,± 2,....

3

Абсциссу, большую 1 , имеют все точки M дуги единичной окружности, 2

лежащие правее прямой M1M2 . Таким образом, решениями неравенства

являются все числа из промежутка − π < x < π .

33

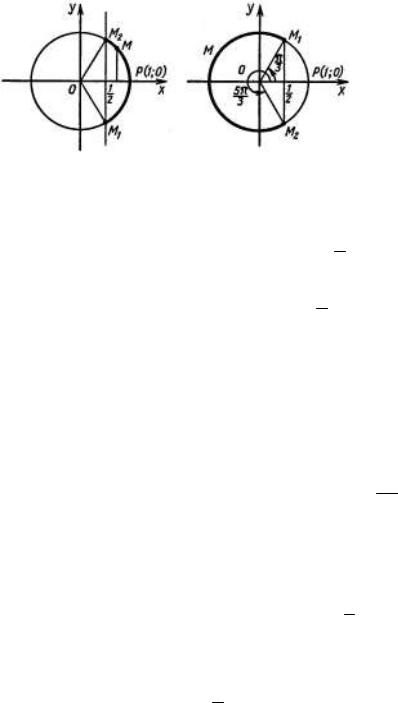
49

Учитывая периодичность функции косинус, получаем, что все решения

данного неравенства – множество интервалов − π + 2πn < x < π + 2πn, n Z.

Рисунок 4.4. Тригонометрическая окружность с отмеченными на ней абсциссами точек М1 и М2

Задача 2. Решить неравенство cosx ≤ 1. 2

Решение. Абсциссу, не большую 1 , имеют все точки дуги единичной 2

окружности M1MM2 (рисунок 4.4, справа). Поэтому решениями неравенства

Учитывая периодичность функции косинус, получаем, что все решения данного

неравенства – множество отрезков π + 2πn ≤ x ≤ 5π + 2πn, n Z.

33

Задача 3. Решить неравенство sin x ≥ − 1. 2

Решение. Синус угла x равен ординате точки единичной окружности.

Ординату, не меньшую − 1 , имеют все точки дуги единичной окружности 2