
6762
.pdf
50
M |
MM |
|
(рисунок 4.5, |
слева). Поэтому решениями неравенства |
sin x ≥ − |
1 |
|
|||||||||||
2 |
|
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
являются |
числа |
|
x, |
|
которые |
принадлежат |
промежутку − π ≤ x ≤ |
7π |
. Все |
|||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
|
|
|
|
решения |
данного |
неравенства |
– |
множество |
|
отрезков |
||||||||||||
− π + 2πn ≤ x ≤ |
7π |
+ 2πn, n Z. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
π |
|
|
7π |
|
|
|
|
|
|
|
|
|
|
Ответ. x |
− |
|
+ 2πn; |
|
+ 2πn , n Z. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|
|
|
|
|
|
|
Рисунок 4.5. Тригонометрическая окружность с отмеченными на ней ординатами (слева) и абсциссами (справа) точек М1 и М2
Задача 4. Решить неравенство sin x < − 1 .
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Решение. Все точки окружности, лежащие ниже прямой |
M1M2 имеют |
|||||||||||
ординату, |
|
|
|
меньшую |
(рисунок |
4.5 слева). Поэтому |
все числа |
||||||
|
|
5π |
|
π |
|
|
|
|
sin x < − |
1 |
|
|
|
x |
− |
|
|
;− |
|
|
являются |
решениями |
неравенства |
|
. |
Все решения |
|
|
|
|
|
||||||||||
|
|
6 |
|
|
6 |
|
|
|
|
|
2 |
|
|
этого неравенства – интервалы |
− |
5π |
+ 2πn;− π + 2πn n Z. |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
6 |
|
|
6 |
|
|
||
|
|
5π |
|
π |
|
|
|
|
|
|
|
||
Ответ. x |
− |
|
+ 2πn;− |
|
|
+ 2πn , n Z. |
|
|
|
||||
|
|
|
|
|
|
||||||||
|
|
6 |
|
6 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
Задача 5. Решить неравенство cos |
|
−1 ≤ − |
|
|
. |
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
4 |
|
2 |
|
||

|
|
|
|
|
|
|
|
|
|
|
51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Обозначим |
x |
|
−1 = y . Решая неравенство cos y ≤ − |
2 |
|
(рисунок |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
4.5, справа), |
находим |
3π |
|
+ 2πn ≤ y ≤ |
5π |
+ 2πn, n Z. |
Заменяя |
|
y = |
x |
−1, |
||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|||||
получаем |
3π |
+ 2πn ≤ |
x |
−1≤ |
5π |
+ 2πn, |
откуда 1+ |
3π |
+ 2πn ≤ |
x |
≤ 1+ |
5π |
+ 2πn, |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
4 |
4 |
|
4 |
|
4 |
|
4 |
|
|
|
4 |
|
|
|
|||||||||||
4 + 3π + 8πn ≤ x ≤ 4 + 5π + 8πn, n Z. 4
Ответ. x [4 + 3π + 8πn;4 + 5π + 8πn], n Z.
Упражнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Решить неравенства |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.1. cos x ≥ |
|
2 |
; |
|
|
1.2. cosx < |
|
3 |
; |
|
||||
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
1.3. cosx > − |
3 |
; |
1.4. cosx ≤ − |
|
2 |
. |
||||||||
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
2 |
|
||||||
2. Решить неравенства |
|
|
|
|
|
|
|
|||||||
2.1. cosx ≤ |
|
|
|
|
2.2. cos x < −2; |
|||||||||
3; |
|
|
||||||||||||
2.3. cos x ≥ 1; |
|
|
|
|
|
|
2.4. cosx ≤ −1. |
|||||||
3. Решить неравенства |
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1. sin x > |
; |
|
|
|
|
3.2. sin x ≤ |
|
2 |
; |
|
||||
|
||||||||||||||
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
3.3. sin x ≤ − |
|
2 |
; |
3.4. sin x > − |
3 |
. |
||||||||
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
2 |
|
||||||
4. Решить неравенства |
|
|
|
|
|
|
||||||||
4.1. sin x ≥ − |
|
|
|
4.2. sin x > 1; |
|
|
|
|
||||||
2; |
|
|
|
|
||||||||||
4.3. sin x ≤ −1; |
4.4. sin x ≥1. |
|
|
|
|
|||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Решить неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
5.2. 2sin 3x > −1; |
|
|
|
|
|
|
|||||||||||||
5.1. |
|
2 |
cos2x ≤1; |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
||||||||||
5.3. |
sin x + |
|
|
≤ |
|
|
|
; |
5.4. |
cos x − |
|
≥ |
|
|
|
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
6 |
|
|
2 |
|
|
|
|
||||
6. Решить неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
|
|
+ 2 |
≥ |
|
|
|
|
|
|
2 |
|
||||||||||||||
6.1. |
cos |
|
|
|
; |
|
6.2. |
sin |
|
|
− |
3 < − |
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
2 |
|
|
||||
|
7. Решить неравенства |
|
|
|
|
|
|
|
|||||
|
7.1. sin2 x + 2sin x > 0; |
|
7.2. cos2 x − cosx < 0. |
|
|
||||||||
|
Ответы. |
1.1. |
− π + 2πn ≤ x ≤ π + 2πn , |
|
n Z.; |
1.2. |
|||||||
|
|
|
|
|
|
4 |
4 |
|
|
|
|
||
π + 2πn ≤ x ≤ |
11π |
|
+ 2πn , |
n Z; 1.3. |
− |
5π |
+ 2πn < x < |
5π |
+ 2πn , |
n Z; |
1.4. |
||
|
|
|
|||||||||||
6 |
|
|
6 |
|
|
|
6 |
|
6 |
|
|
|
|
3π |
+ 2πn ≤ x ≤ |
5π |
+ 2πn , |
n Z. 2.1. |
решений нет; 2.2. решений |
нет; |
2.3. |
||||||
|
|
||||||||||||
44
x = 2πk, |
k Z; 2.4. x = π + 2πk, |
k Z. 3.1. π + 2πn < x < |
5π |
+ 2πn , |
n Z; 3.2. |
||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
6 |
6 |
|
|
|
|||
− |
5π |
+ 2πn ≤ x ≤ π + 2πn , |
n Z; |
3.3. |
− |
5π |
+ 2πn < x < − π + 2πn , n Z.; |
3.4. |
|||||||
|
|
||||||||||||||
4 |
|
4 |
|
|
|
6 |
|
6 |
|
|
|
||||
− π + 2πn ≤ x ≤ |
4π |
+ 2πn , |
n Z. |
4.1. |
решений |
нет; 4.2. решений |
нет; |
4.3. |
|||||||
|
|||||||||||||||
33
x = −π + 2πn, n Z; 4.4. |
x = π + 2πn, |
n Z. 5.1. π + πn ≤ x ≤ |
7π |
+ πn, n Z; |
||||||||||||
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
2 |
|
8 |
8 |
|
|
|
||
5.2. − |
π |
+ |
2πn |
≤ x ≤ |
7π |
+ |
2πn |
, |
n Z; |
5.3. π + 2πn ≤ x ≤ 2π + 2πn , |
n Z; |
5.4. |
||||
|
|
|
|
|||||||||||||
18 |
3 |
|
18 |
|
|
3 |
|
|
2 |
|
|
|
|
|||
2πn ≤ x ≤ π + 2πn, |
n Z; |
6.1. |
12 − 3π + 8πn ≤ x ≤ 12 −π + 8πn , |
n Z; |
6.2. |
|||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53
− 6 −π + 6πn ≤ x ≤ −6 +π + 6πn , n Z. 7.1. 2πn < x < π + 2πn, n Z; 7.2.
−π + 2πn ≤ x ≤ π + 2πn , n Z. 2 2
Упражнения к разделам 1-6
1. Упростить выражение
|
1+ cos2 α |
|
|
|
|
1 |
|
|
|
|
|
1+ sin2 α |
|
|
|
|
||||||
1.1. |
|
|
|
|
|
− sinα |
|
|
|
tgα ; |
1.2. |
ctgα |
|
|
− cosα . |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
sinα |
|
|
|
|
|
2 |
|
|
|
|
|
cosα |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. Упростить выражение |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
π |
+α |
|
|
π |
|
|
|
|
|
π |
|
|
π |
−α |
|
||||
|
sin |
|
|
− cos |
|
|
+α |
|
|
|
sin |
−α |
+ cos |
|
||||||||
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
4 |
|
|
|||
2.1. |
|
|
|
|
|
|
|
|
|
|
; |
2.2. |
|
|
|
|
|
|
|
. |
||
|
|
π |
+ |
α |
|
|
π |
|
|
|
π |
|
|
π |
−α |
|
||||||
|
sin |
|
|
+ cos |
|
|
+α |
|
|
|
sin |
−α |
− cos |
|
||||||||
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
4 |
|
|
|||
3. Доказать тождество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3.1. 1+ tgα tgβ = |
cos(α − β ) |
; |
3.2. tgα − tgβ = |
|
|
sin(α − β ) |
. |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
cosα cos β |
|
|
|
|
|
|
|
|
cosα cos β |
|||||||||
4. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
π |
|
|
|
|
|
|
|
5π |
|
|
|
|
|
|
|
|
|
||
4.1. 2sin 6α cos |
|
|
+ 3α |
− sin 6α |
при α = |
|
|
|
; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|||
4.2. cos3α + 2cos(π − 3α ) sin |
2 |
π |
|
|
|
|
|
|
5π |
|
|
|
||||||||||||
|
|
−1,5α при |
|
α = |
|
|
|
|
. |
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
36 |
|
|
|
|
|||
5. Вычислить |
|
|
|
|
|
|
|
|
|
2cos2 π −1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
3(cos750 − cos150 ) |
|
|
5.2. |
|
|
|
|
|
|
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
π |
|
2 π |
|
|
|||||||||||||
5.1. |
|
|
|
|
|
|
|
; |
|
|
|
1+ 8sin |
2 |
|
|
|
|
|||||||
|
|
1− 2sin2 150 |
|
|
|
|
|
cos |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
||||

|
|
|
|
54 |
|
|
|
|
|
6. |
Доказать тождества |
|
|
|
|
|
|
||
|
|
2sin 2α − sin 4α |
2 |
|
2cos 2α − sin 4α |
|
2 |
π |
|
6.1. |
|
= tg α ; |
6.2. |
|
= tg |
|
|
− α . |
|
2sin 2α + sin 4α |
2cos 2α + sin 4α |
|
|||||||
|
|
|
|
|
|
4 |
|
||
7. |
Показать, что |
|
|
|
|
|
|
|
|
7.1. sin350 + sin 250 = cos50 ; |
7.2. cos120 − cos480 = sin180 . |
|
|||||||
Проверочная работа |
|
|
|
|
|||||||
1. Найти значения выражений |
|
|
|
||||||||
|
1+ cos2α − sin 2α |
при α = |
7π |
|
sin 750 + sin150 |
||||||
|
|
|
|
; |
|
; |
|||||
|
cos2α + cos(0,5 + α ) |
3 |
cos150 − cos750 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
|
||||
arccos − |
|
+ arcsin |
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
2 |
|
2 |
|
|
|
|
|
||
2. Решить уравнения
sin3x cosx − sinx cos3x =1;
2cos2 x + 5cosx = 3; tgx − 3ctgx = 0 ; sin3x − sinx = 0 ; 2sinx + sin2x = 0.
3. Решить неравенства sin x > 1 ; cosx < 0.
2
8. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
||||
8.1. 2arcsin |
|
|
|
+ 3arcsin |
− |
|
; |
8.2. arcsin |
|
|
|
− 4arcsin1; |
||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
− arcsin |
|
3 |
|
|
8.4. arccos(−1)− arcsin(−1); |
|||||||||
8.3. arccos |
|
|
|
|
|
|
; |
|
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(−1)+ 3arctg |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
8.5. 2arctg1− |
3arctg − |
|
|
|
|
; |
8.6. 4arctg |
3 . |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9.1. cos(4 − 2x)= |
; |
|
|
|
|
9.2. cos(6 + 3x)= − |
|
2 |
; |
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9.3. |
|
|
|
|
|
π |
|
= 0 ; |
9.4. |
π |
− 3x |
|
− |
|
|
|
|
|
= 0. |
|||||||||||
|
|
|
|
3 |
|
|||||||||||||||||||||||||
|
2 cos 2x + |
|
|
+1 |
2cos |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
x |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|||
10.1. |
2sin 3x |
− |
|
|
|
+1 = 0 |
|
; |
10.2. |
1− sin |
|
|
+ |
|
|
= 0; |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
10.3. 3 + 4sin(2x +1)= 0 ; |
|
10.4. 5sin(2x −1)− 2 = 0. |
|
|
|
|||||||||||||||||||||||||
11. Решить уравнения
11.1.(1+ 
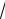 2cosx)(1− 4sin x cosx)= 0;
2cosx)(1− 4sin x cosx)= 0;
11.2.(1− 
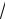 2cosx)(1+ 2sin2x cos2x)= 0.
2cosx)(1+ 2sin2x cos2x)= 0.
12. Решить уравнения
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
1 |
|
|
12.1. |
tg 2x |
+ |
|
= −1; |
|
12.2. |
tg |
3x − |
|
= |
|
|
; |
|||||
|
|
|
|
|||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
|
π |
|
1 |
|
|
|
|
|
π |
|
|
|
|
|
||
12.3. |
tg 3x |
− |
|
= |
|
|
|
; |
12.4. 1− tg x |
+ |
|
= 0. |
|
|
|
|||
|
|
|
|
|
|
|
||||||||||||
|
|
|
4 |
|
3 |
|
|
|
|
|
7 |
|
|
|
|
|
||
13. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|||||||
13.1. 2sin2 x + sin x = 0; |
13.2. 3sin2 x − 5sin x − 2 = 0 ; |
|||||||||||||||||
13.3. cos2 x − 2cosx = 0; |
13.4. 6cos2 x + 7cosx − 3 = 0. |
|||||||||||||||||
14. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|||||||
14.1. 6sin2 x − cosx + 6 = 0 ; |
14.2. |
8cos2 x −12sin x + 7 = 0. |
||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
|
|
|
|
|
|
|
|
|
|
|
|
15. |
Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
15.1. tg2x + 3tgx = 0; |
|
|
|
|
|
|
15.2. 2tg2x − tgx − 3 = 0 ; |
||||||||||||||||||||||||||
15.3. tgx −12ctgx +1= 0 ; |
|
|
|
|
15.4. tgx + ctgx = 2. |
||||||||||||||||||||||||||||
16. |
Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
16.1. 2sin2x = 3cos2x ; |
|
|
|
|
16.2. |
|
4sin3x + 5cos3x = 0. |
||||||||||||||||||||||||||
17. |
Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
17.1. 5sin x + cosx = 5; |
|
|
|
|
|
|
17.2. |
|
4sin x + 3cosx = 6. |
||||||||||||||||||||||||
18. |
Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
18.1. sin3x = sin5x ; |
|
|
|
|
|
18.2. cosx = cos3x ; |
|||||||||||||||||||||||||||
18.3. cos2 3x − cos3x cos5x = 0; |
18.4. sin3x sin5x − sin2 5x = 0. |
||||||||||||||||||||||||||||||||
19. |
Решить неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
19.1. sin x ≥ − |
3 |
|
; |
|
|
19.2. sin x < |
|
|
2 |
; |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
19.3. cosx ≤ |
|
3 |
; |
|
|
|
|
19.4. cosx > − |
|
2 |
. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
20. |
Упростить выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
cosβ |
+ |
sinβ |
|
|
|
|
|
1− cos4α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
cosα |
|
|
|
− β |
+α ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
sinα |
|
|
|
|
|
cos(π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
21. |
Доказать тождества |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
sin(2α − 3π )+ 2cos |
7π |
+ 2α |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − 3ctg |
2 |
4α ; |
||||||||||||||
2cos π − 2α |
+ |
|
cos(2α − 3π ) |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
57 |
|
|
|
|
|
|
|
21.2. |
|
|
4sin2 (α −1,5π ) |
|
|
= −2ctg2 4α ; |
|||||||
|
|
|
|
|
|||||||||
sin4 (α − 2,5π )+ cos4 (α − 2,5π )−1 |
|||||||||||||
21.3. |
|
|
4sin2 (α −1,5π ) |
|
|
= −2ctg2 4α ; |
|||||||
|
sin4 (α − 2,5π )+ cos4 (α − 2,5π )−1 |
|
|||||||||||
|
|
2cos π |
− 2α − |
|
sin(2,5π − 2α )+ |
|
|
|
|
||||
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
tg2α |
|||||
|
|
6 |
|
|
|
|
= |
||||||
21.4. |
|
|
|
|
|
|
|
. |
|||||
|
2cos(4,5π − 2α )+ 2cos π |
+ 2α |
|
|
|
|
|||||||
|
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
22. Доказать тождества
22.1. |
|
1− cosα + cos2α |
|
|
= ctgα ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
sin 2α − sinα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
sinα + sinα |
|
|
|
|
|
|
= tgα ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
22.2. |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1+ cosα + cos |
α |
α |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
22.3. |
cos3α + cos2α + cosα +1 |
= 2cos |
3α |
cosα ; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
cosα + 2cos |
2 |
|
|
α |
−1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2sinα − sin3α + sin5α |
= − |
2cos2α |
|
|
|
|
|
||||||||||||||||||||||
22.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||
|
|
cosα − 2cos2α + cos3α |
|
tg |
α |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23. Упростить выражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2(cosα + cos3α ) |
|
|
|
|
|
|
1+ sinα − cos2α − sin3α |
||||||||||||||||||||||
23.1. |
|
|
|
|
|
|
|
|
; 23.2. |
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
2sin2α + sin 4α |
|
|
2sin2 α − sinα −1 |
|||||||||||||||||||||||||||
24. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
24.1. |
|
|
|
|
|
|
|
; |
|
|
|
|
|
24.2. cos arccos |
|
|
|
; |
|
|
||||||||||||
cos arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||
24.3. sin arccos |
|
|
; |
|
|
|
|
|
|
24.4. |
sin arccos |
|
|
|
|
|
|
|
; |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
58 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|||||||
|
tg arccos |
|
. |
|||||
24.5. tg arccos |
|
; |
24.6. |
|
|
|
||
|
|
|
|
|||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||
25. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||
25.1. sin(4arcsin1); |
|
|
25.2. |
sin 3arcsin |
|
|
|
|
|
|
|
; |
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
25.3. cos 5arcsin |
|
|
|
|
; |
25.4. cos(6arcsin1); |
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
tg |
|
|
|
. |
|
||||||||||
25.5. tg 2arcsin |
|
|
; |
|
|
25.6. |
4arcsin |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
26. Решить уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
26.1. sin2x + 2cos2x =1; |
|
|
26.2. cos2x + 3sin2x = 3. |
|||||||||||||||
27. Решить уравнения
27.1.3sin2 x + sin xcosx − 2cos2 x = 0;
27.2.2sin2 x + 3sin xcosx − 2cos2 x = 0.
28. Решить уравнения |
|
|
|
|
|
|
|
||||
28.1. 1+ 2sin x = sin2x + 2cosx ; |
28.2. 1+ 3cosx = sin2x + 3sin x . |
||||||||||
29. Решить уравнения |
|
|
|
|
|
|
|
||||
29.1. |
|
π |
|
|
π |
=1+ cos2x ; |
|||||
sin x + |
|
+ cos x + |
|
||||||||
|
|
6 |
|
|
3 |
|
|
|
|
|
|
29.2. |
|
π |
|
|
π |
= sin2x . |
|||||
sin x − |
|
|
+ cos x − |
|
|||||||
|
|
4 |
|
|
4 |
|
|
|
|
|
|
30. Решить уравнения |
|
|
|
|
|
|
|
||||
30.1. cos3 xsin x − sin3 xcos x = |
1 |
; |
30.2. sin3 xcos x + cos3 xsin x = |
1 |
. |
||||||
|
|
||||||||||
|
|
|
|
|
|
4 |
|
4 |
|
||

|
|
|
59 |
|
|
31. Решить уравнения |
|
|
|
|
|
31.1. sin2 x + sin2 2x =1; |
|
31.2. |
sin2 x + cos2 2x =1; |
||
31.3. sin 4x = 6cos2 2x − 4 ; |
|
31.4. |
2cos2 3x + sin5x =1. |
||
32. Решить уравнения |
|
|
|
|
|
32.1. sin2 x − cos xcos3x = |
1 |
; |
32.2. |
sin3x = 3sinx ; |
|
4 |
|||||
|
|
|
|
||
32.3. 3cos2x − 7sin x = 4; |
|
|
32.4. |
1+ cosx + cos2x = 0; |
|
32.5. cos4x − sin2x =1; |
|
|
32.6. 5sin 2x + 4cos3 x − 8cosx = 0. |
||
33. Решить уравнения
33.1.sin x + cosx = 
 2sin7x ;
2sin7x ;
33.2.sin x + sin2x + sin3x = 0;
33.3.sin x − sin3x = sin2x − sin4x ;
33.4.cosx − cos3x = cos2x − cos4x.
|
|
Ответы. 1.1. cosα ; 1.2. 2sinα . 2.1. tgα ; |
2.2. − сtgα . 4.1. − |
1 |
; 4.2. |
|
1 |
; |
||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
. 8.1. π ; 8.2. − |
7π |
; 8.3. π ; 8.4. |
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
; 8.5. 0; 8.6. 0; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
5.1. 2 ; 5.2. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9.1. |
|
|
|
x = ± π + 2 −πk , |
|
k Z; |
9.2. |
x = −2 ± π − |
2πk |
, |
k Z; |
|
|
9.3. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||
x = ± |
3π |
− π −πk, |
k Z; |
|
9.4. |
|
|
x = π ± |
π |
+ |
2πk |
, |
|
|
k Z. |
10.1. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
18 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x = (−1)k+1 |
π |
+ |
|
π |
+ πk , |
|
k Z; |
|
|
|
10.2. |
|
|
|
|
|
|
x = π + 4πk , |
k Z; |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
18 |
|
12 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||
10.3.x = (−1)k+1 |
1 |
arcsin |
3 |
− |
1 |
+ πk , |
k Z; |
10.4. |
|
|
x = |
1 |
+ (−1)k |
1 |
arcsin |
2 |
+ πk , |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
5 |
|
2 |
|
|||||||||||||
k Z. |
11.1. |
|
|
|
x = ± |
3π |
+ 2πk, x = (−1)k |
π |
+ πk , |
|
|
k Z; |
11.2. |
|
x = ± π + 2πk, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
12 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||
