
6388
.pdf
60
Пример. Точка M (6,-2
 2 ) лежит на гиперболе, уравнения асимптот которой
2 ) лежит на гиперболе, уравнения асимптот которой
y = ± 2 x . Составить уравнение гиперболы и построить ее.
3 |
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Каноническое уравнение гиперболы |
x 2 |
- |
y 2 |
=1, т.к. асимптоты |
|||||||||
a 2 |
b 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
y = ± |
2 |
x , то |
b |
= |
2 |
, b = |
2 |
a . Подставим последнее в уравнение гиперболы: |
|||||
|
|
|
|
||||||||||
3 |
|
a 3 |
3 |
|
|
|
|
|
|||||
y
2
 2
2
- 3 2 |
3 2 |
x |
|
|
- 2
 2
2
|
x 2 |
- |
y 2 |
× 9 =1, далее т. M (6,-2 |
|
)лежит на гиперболе, т.е. |
36 |
- |
8 × 9 |
=1 , |
|||||||||||||
|
2 |
||||||||||||||||||||||
|
a 2 |
4a 2 |
a 2 |
4a 2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
144 - 72 |
|
=1, 72 = 4a 2 , |
a2 =18 , |
|
a = 3 |
|
; тогда b = |
2 |
× 3 |
|
= 2 |
|
|
|
|||||||||
|
|
2 |
2 |
|
2 . Итак, иско- |
||||||||||||||||||
|
|
4a 2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||
мое уравнение |
x 2 |
- |
y 2 |
=1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
18 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
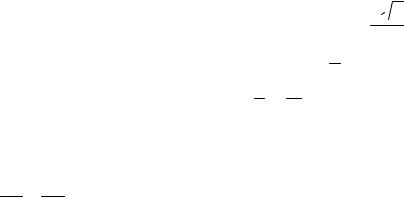
61
Задания для самостоятельной работы:
1.Пользуясь определением гиперболы, составить её уравнение, если
известно, что точки F1 (− 2 ; 0) и F2 (2 ; 0) являются фокусами гиперболы, а длина большой оси равна 2.
2.Пользуясь определением гиперболы, составить её уравнение, если
известно, что точки F1 (0 ; − 3) и F2 (0 ; 3) являются фокусами гиперболы, а длина большой оси равна 4.
3. |
Построить гиперболу 16x 2 − 9 y 2 =144 . |
Найти: 1) действительную и |
мнимую полуоси; 2) координаты фокусов; 3) |
эксцентриситет; 4) уравнения |
|
асимптот. |
|
|
4.Составить уравнение гиперболы, проходящей через точку M (9 ; 8 ), если
асимптоты гиперболы имеют уравнения y = ± 2  2 x . 3
2 x . 3
5.Эксцентриситет гиперболы ε = 
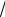 2 . Составить уравнение гиперболы,
2 . Составить уравнение гиперболы,
проходящей через точку M (
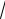 3 ;
3 ; 
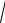 2 ).
2 ).
6. Найти расстояние между фокусами и эксцентриситет гиперболы
x 2 − y 2 = 1
164
7.Действительная полуось гиперболы равна 5, эксцентриситет ε = 1,4 . Найти уравнение гиперболы.
8.Составить каноническое уравнение гиперболы, зная, что расстояние между фокусами равно 14, а расстояние между вершинами равно 12.
9. |
Найти эксцентриситет гиперболы |
x 2 |
− |
y 2 |
=1. |
|
|
||||
|
|
9 |
16 |
|
|
10.Составить каноническое уравнение гиперболы, фокусы которой лежат на
оси OX симметрично относительно начала |
координат, если дана точка |
||
M (4 ,5 ; −1 ) гиперболы и уравнения асимптот |
y = ± |
2 |
x . |
|
|||
|
3 |
|
|

62 |
|
|
|
|
11. Фокусы гиперболы совпадают с фокусами эллипса |
x 2 |
+ |
y 2 |
=1. |
|
|
|||
25 |
16 |
|
||
Составить уравнение гиперболы, если ее эксцентриситет ε =1,5 .
12.Составить уравнение гиперболы, вершины которой находятся в фокусах
эллипса |
x 2 |
+ |
y 2 |
= 1 , а фокусы – в вершинах данного эллипса. |
|
|
|||
25 |
9 |
|
||
Определить область расположения кривых и построить их:
|
2 |
|
|
|
|
|
|
x = − |
4 |
|
|
|
x = |
2 |
|
|
|
|
1) y = |
|
x 2 − 9 ; 2) |
|
|
|
y 2 + 9 ; 4) |
|
y 2 + 25 |
||||||||||
|
y = −3 x 2 +1 ; 3) |
|
||||||||||||||||
|
|
|
||||||||||||||||
3 |
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
||||
13. Найти точки |
пересечения асимптот |
гиперболы x 2 − 3 y 2 =12 с |
||||||||||||||||
окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.
14.Определить траекторию точки M , которая движется так, что остается
вдвое дальше от точки F (− 8;0), чем от прямой x =−2.
15.Найти каноническое уравнение гиперболы, асимптотами которой
являются прямые |
y = ±x , а фокусы совпадают |
с фокусами эллипса |
||||
|
x 2 |
+ |
y 2 |
= 1. |
|
|
|
|
|
|
|
||
64 |
28 |
|
|
|
||
16. |
|
Найти расстояния от центра окружности |
x 2 + y 2 − 6 x + 4 y = 0 до |
|||
асимптот гиперболы |
x 2 − y 2 = 9 . |
|
||||
Парабола
Параболой называется множество всех точек плоскости, каждая из кото- рых одинаково удалена от данной точки, называемой фокусом, и данной пря-
мой, называемой директрисой. Расстояние от фокуса |
F до директрисы d |
называется параметром параболы и обозначается через |
p ( p > 0). |
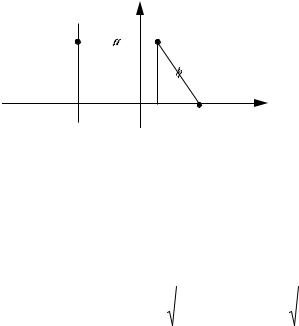
Для вывода уравнения параболы выберем систему координат Oxy так,
чтобы ось Ox проходила через фокус F перпендикулярно директрисе в направ-
63
лении от директрисы к F , а начало координат расположим посередине между фокусом и директрисой (см. рис. 8). В выбранной системе фокус F имеет ко-
ординаты ( |
p |
, 0) , а уравнение директрисы имеет вид |
x = − |
p |
или |
x + |
p |
= 0. |
||
|
|
|
||||||||
2 |
|
|
|
2 |
|
2 |
|
|||
|
|
|
y |
|
|
|
|
|
|
|
|
|
N |
|
M ( x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
x |
|
Рис. 8 |
|||||||||||||
|
x = − |
p |
|
F ( |
p |
,0) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть M |
- произвольная точка параболы. Соединим точку M с F . Прове- |
|||||||||||||||||
дем отрезок MN перпендикулярно директрисе. Согласно определению парабо- |
||||||||||||||||||
лы MF = MN. Используя формулу расстояния между двумя точками, находим: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x − |
|
p |
) 2 + y 2 = (x + |
p |
) 2 |
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
2 . |
|
||||||||||
Возведя обе части уравнения в квадрат, получим |
||||||||||||||||||
|
|
|
|
x 2 − px + |
p 2 |
+ y 2 = x 2 + px + |
p 2 |
, |
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
4 |
|
4 |
|
|||||||||||
т.е.
y 2 = 2 px.
(10)
Уравнение (10) называется каноническим уравнением параболы.
Установим форму параболы, пользуясь его каноническим уравнением.
1. Уравнение (10) содержит y только в четной степени, следовательно парабола симметрична относительно оси Ox , ось Ox называется осью симметрии пара- болы.
64
2. Так как p > 0, то из (10) следует, что x ³ 0. Следовательно, парабола распо-
ложена справа от оси Oy .
3. При x = 0 имеем y = 0. Следовательно, парабола проходит через начало коор-
динат.
y
|
N |
|
|
∙ |
M ( x, |
y) |
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
∙ |
p |
|
x |
||
|
|
|
|
|
|
|
|
|
|
F |
|
,0 |
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
− |
p |
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9 |
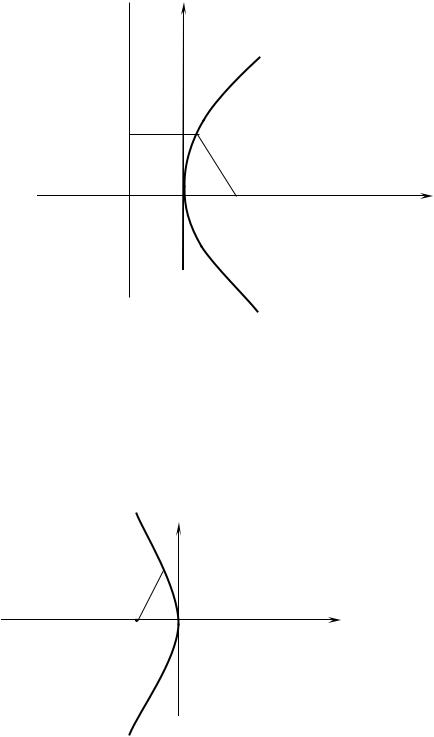
4. При неограниченном возрастании x модуль y |
также неограниченно возрас- |
|||||||||||||
тает. Парабола y 2 |
= 2 px |
имеет вид, |
изображенный на рисунке 9. Точка O(0,0) |
|||||||||||
называется вершиной параболы. |
|
|
|
|||||||||||
Уравнение вида |
y 2 |
= −2 px |
определяет параболу, для которой x £ 0 , т.е. |
|||||||||||
график этой параболы |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M(x,y) |
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
p |
|
|
|
|
|||||
|
− |
p |
|
|
|
|
x |
|
||||||
F |
|
|
,0 |
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения x 2 = 2 py и x 2 = −2 py задают параболы симметричные относи- тельно оси oy :

65
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
N |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
0 |
M |
|
x |
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
F 0, |
|
|
|
|
|
|
|
|
p |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
M |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
F 0,− |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
x |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
p |
N |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
«Вырождения» параболы: |
|
|
|
|
||||
1. |
x 2 |
= −k 2 , |
|
y 2 |
= -k 2 . Эти уравнения не определяют никакого точечного мно- |
|||||||||||||
|
жества при k ¹ 0 . |
|
|
|
|
|
|
|
|
|
|
|||||||
2. |
x 2 |
= k 2 , |
|
y 2 |
= k 2 , эти уравнения определяют пару параллельных прямых: |
|||||||||||||
|
x = ±k и y = ±k . При k = 0 эти прямые совпадают. |
|
|
|
|
|||||||||||||
Пример. Парабола, симметричная относительно оси oy , имеет вершину в начале координат и проходит через точку (6,-2). Написать уравнение параболы и определить координаты ее фокуса.
Решение. Уравнение параболы, |
симметричной относительно оси oy : |
x 2 = 2 py либо x 2 = -2 py . Подставим координаты точки в оба уравнения: |
|
62 ¹ 2 p ×(- 2), т.к. p > 0 . |
62 = -2 p × (- 2) |
|
36 = 4 p |
|
p = 9 |
Уравнение параболы x 2 = -18 y , ветви вниз и F (0;−4,5)
y
0 |
6 |
x
-2
F(0;-4,5)
66
Задания для самостоятельной работы:
1.Составить уравнение параболы, симметричной относительно оси OX, с
вершиной в начале координат и проходящей через точку A (− 3 ; − 3).
2.Составить каноническое уравнение параболы, проходящей через начало
|
координат, если ее директриса имеет уравнение x +15 = 0. |
|
3. |
Найти координаты фокуса и уравнение директрисы параболы y 2 = −12x . |
|
4. |
Найти вершину, фокус и директрису параболы |
y = −2x 2 + 8x − 5 и |
|
построить кривую. |
|
5.Составить уравнение параболы, симметричной относительно оси OY, с
вершиной в начале координат и проходящей через точку A (− 2 ; 4).
6. |
Через фокус параболы |
y 2 |
= 12 x |
проведена хорда, перпендикулярная к её |
||
|
оси. Найти длину хорды. |
|
|
|||
7. |
Составить уравнение параболы с вершиной в начале координат, фокус |
|||||
|
которой находится в точке пересечения прямой 5x − 3 y +12 = 0 с осью: |
|||||
|
1) ординат; |
2) абсцисс. |
|
|
||
8. |
Составить |
уравнение |
множества |
точек, одинаково удалённых от точки |
||
|
F (2 ; 0 ) |
и от прямой |
y = 2 . Найти точки пересечения этой кривой с осями |
|||
|
координат и построить её. |
|
|
|||
9. |
Составить уравнение множества точек, одинаково удалённых от начала |
|||||
|
координат |
и от прямой |
x =−4. |
Найти точки пересечения этой кривой с |
||
осями координат и построить её.
10. Камень, брошенный под углом к горизонту, описал дугу параболы и упал на расстоянии 16м. от начального положения. Определить параметр
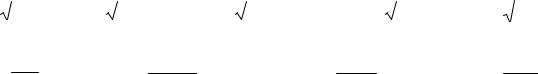
67
параболической траектории, зная, что наибольшая высота, достигнутая камнем, равна 12м.
11.Камень, брошенный под углом к горизонту, достиг наибольшей высоты 16м. Описав параболическую траекторию, он упал в 48м. от точки бросания. На какой высоте находился камень на расстоянии 6м от точки бросания?
12.Зеркальная поверхность прожектора образована вращением параболы вокруг её оси симметрии. Диаметр зеркала 80см, а глубина его 10см. На каком расстоянии от вершины параболы нужно поместить источник света, если для отражения лучей параллельным пучком он должен быть в фокусе параболы?
13.Струя воды фонтана достигает наибольшей высоты 4 м на расстоянии 0,5 м
от вертикали, проходящей через точку O выхода струи. Найти высоту струи
|
над горизонталью OX на расстоянии 0,75 м от точки O . |
14. |
Написать уравнение окружности, диаметром которой служит отрезок, |
|
отсекаемый на оси абсцисс параболой y = 3 − 2x − x 2 . Построить обе кривые. |
15. |
Составить уравнение окружности, имеющей центр в фокусе параболы |
|
y 2 = −6 x и касающейся ее директрисы. |
|
|
|
|
|
|
|||||||
16. |
Написать уравнение окружности с центром в фокусе параболы y 2 = −4 x и |
|||||||||||||
|
радиусом, равным фокусному расстоянию гиперболы |
7 x 2 − 9 y 2 = 63 . |
||||||||||||
17. |
Построить кривые, найдя дополнительные точки |
пересечения с осями |
||||||||||||
|
координат: |
|
|
|
|
|
|
|
|
|
|
|
||
|
1) 3 y = 9 − x 2 ; |
2) y 2 = 9 − 3x ; 3) y 2 = 4 + x ; |
4) |
x 2 = 4 + 2 y . |
||||||||||
18. |
Установить, какие линии определяются следующими уравнениями и |
|||||||||||||
|
построить эти кривые |
|
|
|
|
|
|
|||||||
1) y = 2 |
|
|
y = |
|
; 3) y = −3 |
|
|
y = −2 |
|
; 5) x = − |
|
; |
||
x |
; 2) |
− x |
− 2x |
; 4) |
x |
3 y |
||||||||
6) x = 4
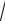 − y ; 7) x = 2 −
− y ; 7) x = 2 − 
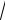 6 − 2 y ; 8) x = −4 + 3
6 − 2 y ; 8) x = −4 + 3
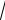 y + 5 ; 9) y = 3 − 4
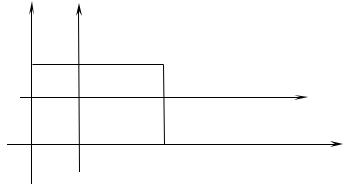
y + 5 ; 9) y = 3 − 4
 x −1 .
x −1 .
68
19. Составить уравнение окружности, имеющей центр в фокусе параболы y 2 = −6 x и касающейся ее директрисы.
Уравнение Ax 2 + Cy 2 + 2Dx + 2Ey + F = 0
Уравнения эллипса, гиперболы, параболы и уравнение окружности мож- но записать с помощью единого уравнения вида
Ax 2 + Cy 2 + 2 Dx + 2Ey + F = 0, |
(1) |
где коэффициенты A и C не равны нулю одновременно.
Теорема 1
Уравнение (1) всегда определяет: либо окружность (при A = C ), либо эллипс (при A ×C > 0 ), либо гиперболу (при A ×C < 0 ), либо параболу (при
A × C = 0 ).
С помощью преобразования параллельного переноса уравнение (1) кри- вой 2-го порядка можно привести к каноническому виду.
Рассмотрим параллельный перенос координатных осей:
|
y |
y′ |
M |
|
|
y ′ |
|
|
|
y |
|
∙ |
|
|
|
|
′ |
x′ |
x′ |
|
|
o (a,b) |
|
|
o |
|
|
x |
x |
|
|
|
|
Рис. 1. |
M (x, y ) – точка с координатами в старой системе координат oxy , M (x′, y′) – точка с координатами в новой системе координат o′x′y′,
O′(a,b) – начало координат новой системы с координатами в старой системе.
Формулы параллельного переноса координатных осей, выражающие ста- рые координаты через новые:
x = x′ + ay = y′ + b
69
Обратные формулы:
x′ = x − ay′ = y − b
Пример 1 С помощью параллельного переноса осей координат привести к каноническому виду уравнение кривой x 2 + 2 y 2 − 4x + 8 y −10 = 0 и построить
ее. |
|
|
|
|
|
|
|
|
Решение. AC > 0 , |
значит уравнение определяет эллипс. Преобразуем дан- |
|||||||
ное уравнение – сгруппируем полные квадраты |
|
|
|
|||||
x 2 − 4x + 4 − 4 + 2(y 2 + 4 y + 4 − 4)−10 = 0 |
|
|
|
|||||
(x − 2)2 + 2(y + 2)2 = 22 |
|
|
|
|||||
(x − 2)2 |
+ (y + 2)2 |
=1 |
|
|
|
|
||
22 |
11 |
|
. |
|
|
|
|
|
Положим x − 2 = x′ эта система задает формулы параллельного переноса |
||||||||
|
|
y + 2 = y′ |
|
|
|
|||
осей координат в т. O1 (2,−2). Получим уравнение эллипса: |
( x′) 2 |
+ |
( y′) 2 |
=1, с по- |
||||
|
|
|||||||
|
|
|
|
22 |
11 |
|
||
луосями a = |
|
, b = |
|
и центром симметрии в т. O1 (2,−2). |
|
|
|
|
22 |
11 |
|
|
|
||||
y |
y ′ |
|
|
0 |
|
|
b |
x |
|
O1 |
|
-a |
a |
x′ |
|
-b
Рис. 2.
