
6282
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
С.Я. Скворцов, А.А. Кочеткова, К.П. Жегалова
Расчет осадки грунтового основания зданий и сооружений с учетом взаимного влияния фундаментов
Учебно-методическое пособие
по:
-подготовке практическим занятиям (включая рекомендации по организации самостоятельной работы);
для обучающихся по дисциплине «Строительные конструкции» направлению подготовки 27.03.01 Стандартизация и метрология профиль – Стандартизация и сертификация
Нижний Новгород
2016
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
С.Я. Скворцов, А.А. Кочеткова, К.П. Жегалова
Расчет осадки грунтового основания зданий и сооружений с учетом взаимного влияния фундаментов
Учебно-методическое пособие
по:
-подготовке практическим занятиям
для обучающихся по дисциплине «Строительные конструкции» направлению подготовки 27.03.01 Стандартизация и метрология профиль – Стандартизация и сертификация
Нижний Новгород ННГАСУ
2016
УДК 624.159.2(075.8)
Скворцов С.Я./ Расчет осадки грунтового основания зданий и сооружений с учетом взаимного влияния фундаментов [Электронный ресурс]: учеб.-метод. пос. / С.Я. Скворцов, А.А. Кочеткова, К.П. Жегалова; Нижегор. гос. архитектур. - строит. ун - т – Н. Новгород: ННГАСУ, 2016. – 33 с.– 1 электрон. опт. диск (CD-RW)
Приведены указания для подготовки к практическим занятиям по дисциплине «Строительные конструкции», рассмотрены примеры расчета осадки с учетом взаимного влияния соседних фундаментов.
Предназначено обучающимся в ННГАСУ для подготовки к практическим занятиям по направлению подготовки 27.03.01 Стандартизация и метрология, профиль – Стандартизация и сертификация
© С.Я. Скворцов, А.А. Кочеткова, К.П. Жегалова, 2016 © ННГАСУ, 2016
|
|
4 |
|
|
|
|
Содержание. |
|
|
|
Введение……………………………………………………………… |
|
|
…… 5 |
1. |
Основные сведения…………………………………… |
…………………..6 |
|
|
2. |
Методика расчета осадки с учетом взаимного влияния |
|
||
|
соседних фундаментов по СНиП 2.02.01-83* «Основания |
|
||
|
зданий и сооружений», СП 50-101-2004 «Проектирование |
|
||
|
и устройство оснований и фундаментов зданий и сооружений» …… |
...9 |
||
3. |
Пример 1: Рядом стоящие столбчатые |
|
|
|
фундаменты ………………… |
……………………………………………….10 |
|
|
|
4. |
Пример 2: Деформационный шов ленточного фундамента………… |
…16 |
||
5. |
Приложение 1…………………………………………………………… |
|
..31 |
|
|
Рекомендуемая литература……………………………………………...32 |
|
|
|
5
Введение
В настоящее время в связи с большой плотностью застройки, вновь воз-
водимые здания и сооружения строятся в непосредственной близости друг от друга или пристраиваются непосредственно к существующим зданиям. В слу-
чае расположения двух или нескольких фундаментов рядом в их основании по-
мимо напряжений от собственной нагрузки развиваются дополнительные напряжения за счет влияния соседних фундаментов. В результате фундаменты получают дополнительные, как правило, неравномерные осадки, которые могут привести к образованию трещин в несущих конструкциях и даже аварии.
В данных методических рекомендациях рассмотрен метод расчета осадки основания с учетом влияния соседнего фундамента рекомендуемый в СНиП
2.02.01-83* «Основания зданий и сооружений». Рассмотрено два примера рас-
чета осадки с учетом взаимного влияния соседних фундаментов:
Пример 1: Рядом стоящих столбчатых фундаментов.
Пример 2: Деформационный шов ленточного фундамента.

6
1. Основные сведения.
Некоторые примеры развития дополнительных осадок от влияния сосед-
них зданий или сооружений приведены на рис 1.1, 1.2, 1.3
1,2 – здания первой и второй очереди строительства соответственно 3 – характерные места появления трещин
4 – эпюра осадок фундаментов
5 – эпюра дополнительных осадок фундамента
Рис. 1.1 Деформации при возведении зданий в несколько очередей
1 – проектное положение зданий
2 – положение зданий после наклона (крена)
3 – границы зоны уплотнения грунта
4 – зона дополнительного уплотнения грунта
Рис. 1.2 Деформации при строительстве смежных высотных зданий
1 – эксплуатируемое здание
2 – дополнительно устанавливаемое оборудование
3 – эпюра осадок фундаментов эксплуатируемого здания 4 – эпюра осадок фундаментов здания после установки тяжелого оборудования 5 – границы зоны уплотнения грунта
6 – положение здания после деформации
Рис. 1.3 Деформации при устройстве фундаментов под тяжелое оборудование
Выражение для величины сжимающих напряжений, при действии равно-
мерно распределенной нагрузки получено А. Лявом, а так же Г.К. Лоттером ко-
торый разработал приём, упрощающий математические выкладки. В.Г. Корот-
кин используя функции напряжений акад. Б.Г. Галеркина получил формулы для всех составляющих напряжений при действии нагрузки равномерно распреде-
ленной и меняющейся по закону треугольника1.
1 по Н.А. Цытовичу «Механика грунтов» 1963г.

7
Приведем формулу А. Лява для величины сжимающих напряжений, отне-
сенных к площадкам, параллельным ограничивающей горизонтальной плоско-
сти. Сжимающее напряжение σz в любой точке, лежащей под центром тяжести загруженного прямоугольника, стороны которого равны 2l1 и 2b1 (рис. 1.4) бу-
дет равно:
|
2 p |
l ×b × z |
|
l 2 |
+ b2 |
+ 2 × z2 |
|
|
l |
|
×b |
|
|
|
|
|
|||||||
sz = |
|
|
1 |
1 |
× |
1 |
1 |
|
|
+ arcsin |
|
|
1 |
|
1 |
|
|
|
|
(1.1) |
|||
p |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
D |
2 |
× z |
2 |
|
2 |
+ z |
2 |
2 |
+ z |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
|
b1 |
|
|
|
|
|||||
Рис. 1.4 Схема действия местной равномерно распределенной нагрузки по прямоугольной площадке.
где:
p – интенсивность внешней равномерно распределенной нагрузки
z – глубина рассматриваемой точки.
|
|
|
|
|
|
|
|
D2 = l 2 |
+ b2 |
+ z2 |
|
|
|
|
|
|
|
|
|
|
|
(1.2) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Сжимающее напряжение σz в угловой точке C будет равно: |
|
|
|
|
|||||||||||||||||||||||||
|
p |
|
l ×b × z |
|
l |
2 |
+ b |
2 |
+ 2 × z |
2 |
|
|
|
|
|
l ×b |
|
|
|
|
|
||||||||
szc = |
|
× |
|
|
|
|
|
+ arcsin |
|
|
|
|
|
|
|
|
(1.3) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2p |
D |
D |
2 |
× z |
2 |
+ l |
2 |
×b |
2 |
|
2 |
+ z |
2 |
2 |
+ z |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
b1 |
|
|
|
|
|||||||||

8
При сравнении выражений (1.1) и (1.2) получается, что сжимающее напряжение в полупространстве для площадок, параллельных ограничивающей плоскости, на некоторой глубине z под углом загруженного прямоугольника равно четверти напряжения под центром прямоугольника на половинной глу-
бине z . 2
Если известно угловое сжимающее напряжение, то по нему легко опреде-
ляются и сжимающие напряжения для любой точки полупространства, исполь-
зуя метод угловых точек.
Метод угловых точек весьма удобен тогда, когда загружаемая площадь легко разбивается на прямоугольники. Здесь могут встретиться три случая:
Рис. 1.5 Схема разбивки прямоугольной площади загрузки при определении сжимающих напряжений по методу угловых точек.
1) точка М находится на контуре прямоугольника давлений (рис. 1.5 а)
Величина σz определяется как сумма двух угловых напряжений, возни-
кающих в рассматриваемой точке от действия нагрузки по прямоугольникам
Mabe и Mdce.
2) точка М находится внутри прямоугольника давлений (рис. 1.5 б)
В этом случае необходимо сложить угловые напряжения от четырех пря-
моугольников Mhde, Mecf, Mfdg, Mgah.
3) точка М находится вне прямоугольника давлений (рис. 1.5 в)
Напряжения в точке М складываются из суммы напряжений от действия нагрузки по прямоугольникам Mhbe и Mecf, взятых со знаком плюс, и напря-
жений от действия нагрузки по прямоугольникам Mhag и Mgdf, взятых со зна-
ком минус.
9
2. Методика расчета осадки с учетом взаимного влияния соседних фундаментов по СНиП 2.02.01-83* «Основания зданий и сооружений», СП
50-101-2004 «Проектирование и устройство оснований и фундаментов зда-
ний и сооружений»
Согласно нормативных документов [1] и [3] помимо определения разме-
ров подошвы фундамента требуется определить и величину осадки грунтового основания. В случае расположения рядом соседнего фундамента необходимым условием является учет взаимного влияния его на рассчитываемый фундамент.
Фактически расчет сводиться к определению дополнительного верти-
кального напряжения от здания
szp,i = szp1,i + szp2,i |
(2.1) |
где: szp1,i = ai × P01 - дополнительное вертикальное нормальное напряже-
ние от здания на глубине Z от фундамента осадку, которого рассчитывают.
k |
|
σzp2,i = ∑σzp,M,i |
(2.2) |
i=1 |
|
k – количество влияющих фундаментов. |
|
szp,M,i - дополнительное вертикальное напряжение на глубине Z |
от i-го |
влияющего фундамента, определяемое алгебраической суммой напряжений
σc |
zp,j |
в угловых точках четырех фиктивных фундаментов (метод угловых то- |
||||
|
|
|
|
|
|
|
чек) (рис. 2.1) |
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
σzp,M |
= ∑σczp,j |
(2.3) |
||
|
|
|
|
j=1 |
|
|
|
|
sc zp,j |
= |
P02 × a j |
|
(2.4) |
|
|
|
||||
|
|
|
4 |
|
|
|
|
|
В расчетах коэффициенты αi |
и α j принимаются по таблице 1. |
прил. 1 |
||
(табл. 5.6 [3]) в зависимости от формы подошвы фундамента и относительной
глубины, равной: ζ = |
2z |
- при определении α |
|
и ζ = |
z |
- при определении α |
|
. |
|
i |
|
j |
|||||
|
b |
|
b |
|
||||
|
|
|
|
|
||||
а) б)
2
|
+ |
1 |
|
А |
А |
|
1 |
10
- |
А |
2
- |
А |
3 |
+ |
А |
4
Рис. 2.1. К определению методом угловых точек дополнительных вертикальных напряжений σc zp,j в основании рассчитываемого фундамента с учетом влияния сосед-
него фундамента
а) расположение рассчитываемого 1 и влияющего 2 фундамента; б) расположение
фиктивных фундаментов 1 – 4
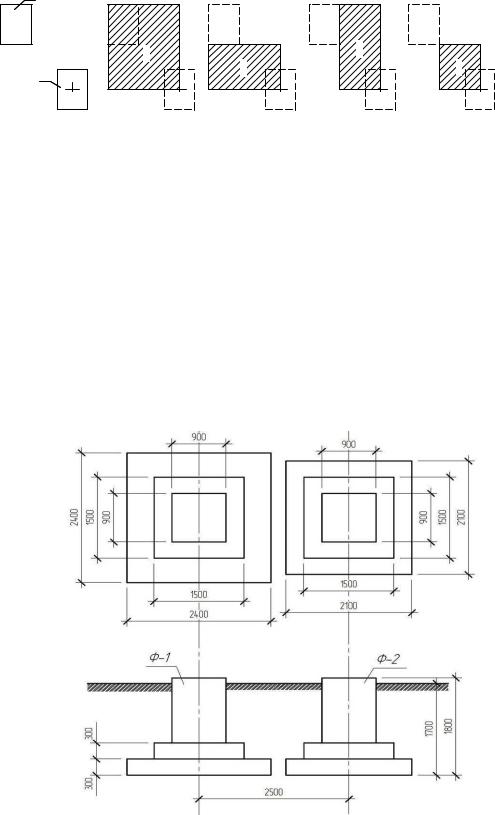
3. Пример 1: Рядом стоящие столбчатые фундаменты.
Определим осадку фундамента Ф-1 с учетом влияния на него соседнего
фундамента Ф-2 (рис. 3.1).
Рис. 3.1. Схема к расчету осадки столбчатого фундамента с учетом влияния соседнего фундамента.
