
5684
.pdf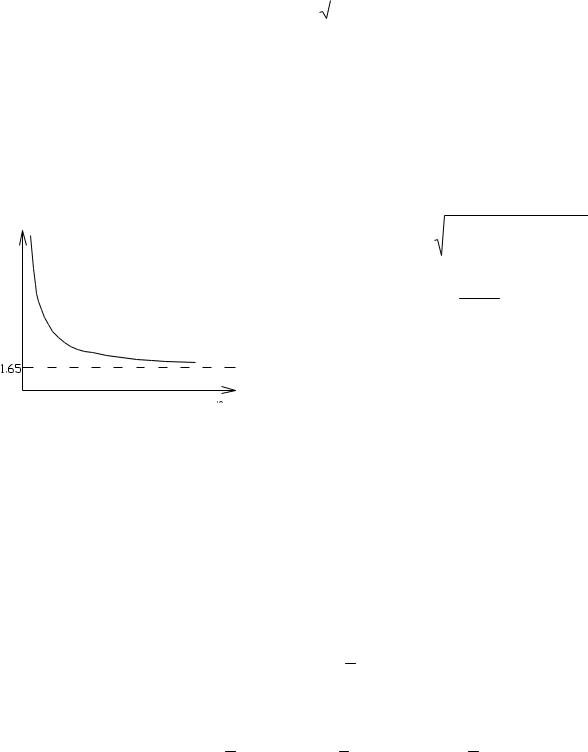
где p p |
|
... p |
|
|
1 |
. R |
|
появляется один раз). |
|
n |
n |
i |
|||||
1 |
2 |
|
|
|
|
pi — вероятность появления возможных значений Ri предела текучести или временного сопротивления;
n — число испытанных образцов (полная группа несовместных событий);f (n) — коэффициент, учитывающий объем выборки.
|
0.91 |
|
1.5 |
|
, |
||||
1.65 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||
|
n |
|
|||||||
|
|
|
|
|
|
||||
при n 3 3.342; n 10 2.372; n 100 1.825;
n1.645 r ,
показывает, на какое число стандартов (R) сдвинуто нормативное сопротивление по
отношению к математическому ожиданию.
Чем больше n, тем достовернее полученные результаты, тем меньше и больше Rn
(Ryn или Run ).
|
(R) |
1 Ri M(R) 2 . |
|
|
|
n |
|
n 1 i 1 |
|
При значении коэффициента вариации
(изменчивости) v(R) (R) 0.1 использовать
M(R)
результаты, полученные из опытов, не допускается, т. к. они ненадежны. Кроме того, коэффициентом надежности по материалу m 1
учитывается разброс (изменчивость в неблагоприятную сторону) найденных
нормативных сопротивлений.
Расчетное сопротивление вычисляется по формулам (здесь – для стальных
конструкций): |
Ry |
|
Ryn |
|
(по пределу текучести); |
|||
|
|
|||||||
|
|
|
|
m |
|
|||
|
|
|
|
|
|
|||
или |
R |
Run |
- по пределу прочности. |
|||||
|
||||||||
|
|
u |
|
|
|
m |
|
|
|
|
|
|
|
|
|
||
Нормативные значения принимаются с обеспеченностью 0.95, т. е. вероятность того, случайное фактическое сопротивление R Rn равна 0.95, т. е.
Rn
P(Rn ) P(x)dx 0.05
или, приняв нормальное распределение, через интеграл вероятности Гаусса Ф(х):
|
1 |
R |
n |
R |
|
||
P(R ) |
|
Ф |
|
|
|
0.05. |
|
|
|
|
|
||||
n |
2 |
|
(R) |
|
|
||
|
|
|
|
||||
Определим математическое ожидание предела текучести для стали С235. Примем v(R) 0.1 (худший вариант), и тогда
|
|
|
1 |
Ryn Ry |
|
|
Ry Ryn |
|
|
Ry |
Ryn |
|
||||
P(R |
yn |
) |
|
Ф |
|
|
|
|
0.05 Ф |
|
|
|
0.45 |
|
|
1.645 |
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
(R) |
|
|
|
(R) |
|
|
|
0.1Ry |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y |
281МПа при Ryn |
235МПа. |
|
|
|
||||
|
|
|
|
|
R |
|
|
|
||||||||

При изменчивости v(R) (R) 0.05 Ry 256МПа.
Ry
Определим, насколько сдвинуто влево от математического ожидания предела текучести Ry расчетное сопротивление по пределу текучести Ry .
m 1.025;v(R) 0.05;Ryn 235МПа; Ry 256МПа;
Ry |
Ryn |
|
|
235 |
230 |
МПа; |
|
m |
1.025 |
||||||
|
|
|
|
||||
Ry Ry 256 230 26МПа;
(R) v(R)Ry 0.05 256 12.8МПа.
Таким образом, расчетное сопротивление сдвинуто влево от математического ожидания
предела текучести |
|
y |
на |
|
|
|
26 |
2 (R) и вероятность того, что предел текучести |
|
R |
|||||||||
|
12.8 |
||||||||
|
|
|
(R) |
|
|
||||
будет меньше расчетного сопротивления Ry равна:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Ry Ry |
1 |
|
230 256 |
|
|
1 |
|
||||
P(R |
) |
|
Ф |
|
|
|
|
|
Ф |
|
|
|
|
Ф(2) 0.0228 |
|
|
|
|
|
|
|
||||||||
y |
|
2 |
|
(R) |
|
|
2 |
|
12.8 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
Обеспеченность расчетного сопротивления этой стали равна
1 P Ry 1 0.0228 0.9772.
Нормами строго установлена обеспеченность расчетных сопротивлений только для древесины и древесных пластиков. Она составляет 0,99. Для бетонов, кирпича и других конструкционных материалов нет единой обеспеченности этой важнейшей прочностной характеристики, используемой при проектировании.
10.2. Влияние износа и изменения прочности во времени
Износ (ржавление, гниение, старение) — изменение прочности конструкции или ее элементов во времени. Если прочность R — случайная величина, то при наличии износа ее следует считать случайной функцией времени R(t).
Запишем S(t) R(t) F(t), где S(t) — случайная функция резерва прочности.
Отказом будет являться переход случайной функции S(t) через нуль в отрицательную область (S(t) 0).
При отсутствии взаимной корреляционной связи между F(t) и R(t) (т. е. F(t) и R(t)
независимы и их взаимная корреляционная функция KFR (t1,t2) 0 (см.(68.5))) математическое ожидание случайной функции S(t) (как детерминированной функции аргумента t):
S(t) R(t) F(t).
Автокорреляционная функция для S(t):
KS (t1,t2 ) KR (t1,t2 ) KF (t1,t2 ).
Дисперсия для функции S(t) при t1 t2 t :
DS (t) DR (t) DF (t).
Аналогично (78.5) временная плотность вероятности того, что S(t) 0:
0
q(0) PSV (0,v)vdv,
где v f (t), вместо аргумента s — значение 0,

PSV (s,v) — совместное распределение значений s 0 и ее производной в данный
момент времени. Знак минус указывает на то, что выбросы происходят в отрицательном направлении.
|
|
|
|
|
v(t) |
dS(t) |
|
dR(t) |
|
dF(t) |
|
|
|
|
|
|
|
|
|
dt |
dt |
|
|
||||
|
|
|
|
|
|
dt |
|
|
|
||||
Если |
приближенно |
считать, что |
случайные ординаты s и v |
функций S(t) |
иV(t) — |
||||||||
независимые случайные величины, то (см. (80.5)): |
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
q(0) PS (0) PV (v)vdv PS (0)v , |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где v — математическое ожидание отрицательной величины v для данного момента |
|||||||||||||
времени; |
|
v |
(t) |
|
|
|
|
|
|
|
|
|
|
q |
зависит от |
t, т. к. |
— математическое |
ожидание |
отрицательной |
скорости |
|||||||
изменения случайной функции S(t).
Если износ практически отсутствует, то прочность не зависит от времени и |
|||||||||||||||
представляет собой не случайную функцию, а случайную величину R. При этом: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
S(t) R F(t) |
|
|
|
|||
и соответственно |
|
(t) |
|
|
|
(t); |
KS (t1,t2 ) D(R) KF (t1,t2 ). |
|
|||||||
S |
R |
F |
|
||||||||||||
Далее: v(t) |
dF(t) |
; т. к. |
dR(t) |
0. |
|
|
|
|
|||||||
dt |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|||
И тогда функция надежности конструкции (вероятность неразрушения за период |
|||||||||||||||
t): |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Pt |
1 PS |
|
|
T |
|
|
|
||
|
|
|
|
|
|
(0) exp |
q(0)dt |
, |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
где PS (0) — интегральная |
функция распределения |
резерва |
прочности S |
в начальный |
|||||||||||
момент времени t 0, (т. |
|
е. |
PS (S) |
при S 0 , |
|
представляющая собой |
вероятность |
||||||||
разрушения в начальный момент времени t 0 или вероятность мгновенного отказа).
11. ХАРАКТЕРИСТИКИ НАГРУЗОК И ВОЗДЕЙСТВИЙ
11.1. Классификация нагрузок
Нагрузки и воздействия представляют собой наиболее неопределенные величины, обладающие большим статистическим разбросом.
Вчасти математического описания нагрузки делятся на:
-нагрузки, представляющие собой случайные величины;
-нагрузки, представляющие собой случайные функции времени;
-нагрузки, изменяющиеся не только во времени, но и в пространстве по случайным или детерминированным законам.
По продолжительности действия и частоте появления действующий СНиП 2.01.07-
85* разделяет нагрузки на постоянные и временные (длительные, кратковременные, особые).
К постоянным нагрузкам относятся:
а) вес частей сооружений, в том числе вес несущих и ограждающих строительных конструкций;
б) вес и давление грунтов (насыпей, засыпок), горное давление.
Сохраняющиеся в конструкции или основании усилия от предварительного напряжения следует учитывать в расчетах как усилия от постоянных нагрузок.
К длительным нагрузкам относятся:
а) вес временных перегородок, подливок и подбетонок под оборудование; б) вес стационарного оборудования: станков, аппаратов, моторов, емкостей, трубопроводов с
арматурой, опорными частями и изоляцией, ленточных конвейеров, постоянных подъемных машин с их канатами и направляющими, а также вес жидкостей и твердых тел, заполняющих оборудование;
в) давление газов, жидкостей и сыпучих тел в емкостях и трубопроводах, избыточное давление и разрежение воздуха, возникающее при вентиляции шахт;
г) нагрузки на перекрытия от складируемых материалов и стеллажного оборудования в складских помещениях, холодильниках, зернохранилищах, книгохранилищах, архивах и подобных помещениях;
д) температурные технологические воздействия от стационарного оборудования; е) вес слоя воды на водонаполненных плоских покрытиях;
ж) вес отложений производственной пыли, если ее накопление не исключено соответствующими мероприятиями;
з) нагрузки от людей, животных, оборудования на перекрытия жилых, общественных и сельскохозяйственных зданий с пониженными нормативными значениями, приведенными в табл. 3 СНиПа;
и) вертикальные нагрузки от мостовых и подвесных кранов с пониженным нормативным значением, определяемым умножением полного нормативного значения вертикальной нагрузки от одного крана в каждом пролете здания на коэффициент:
0,5 — для групп режимов работы кранов 4К - 6К; 0,6 — для группы режима работы кранов 7К; 0,7 — для группы режима работы кранов 8К.
Группы режимов работы кранов принимаются по ГОСТ 25546—82; к) снеговые нагрузки с пониженным расчетным значением, определяемым умножением
полного расчетного значения на коэффициент 0,5.
л) температурные климатические воздействия с пониженными нормативными значениями, определяемыми в соответствии с указаниями пп. 8.2—8.6 СНиПа
м) воздействия, обусловленные деформациями основания, не сопровождающимися коренным изменением структуры грунта, а также оттаиванием вечномерзлых грунтов;
н) воздействия, обусловленные изменением влажности, усадкой и ползучестью материалов.
К кратковременным нагрузкам следует относить:
а) нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательном режимах, а также при его перестановке или замене;
б) вес людей, ремонтных материалов в зонах обслуживания и ремонта оборудования; в) нагрузки от людей, животных, оборудования на перекрытия жилых, общественных и
сельскохозяйственных зданий с полными нормативными значениями; г) нагрузки от подвижного подъемно-транспортного оборудования (погрузчиков,
электрокаров, кранов-штабелеров, тельферов, а также от мостовых и подвесных кранов с полным нормативным значением);
д) снеговые нагрузки с полным расчетным значением; е) температурные климатические воздействия с полным нормативным значением; ж) ветровые нагрузки; з) гололедные нагрузки.
К особым нагрузкам следует относить: а) сейсмические воздействия; б) взрывные воздействия;
в) нагрузки, вызываемые резкими нарушениями технологического процесса, временной неисправностью или поломкой оборудования;
г) воздействия, обусловленные деформациями основания, сопровождающимися коренным изменением структуры грунта (при замачивании просадочных грунтов) или оседанием его в районах горных выработок и в карстовых.

11.2. Нагрузки как случайные величины
11.2.1. Снеговые нагрузки
Для расчета сооружений на длительные сроки требуется значение максимальной снеговой нагрузки за много лет. Поскольку корреляция между годовыми нагрузками практически отсутствует, многолетнюю снеговую нагрузку можно получить теоретически, зная функцию распределения максимальной годовой нагрузки.
Обычно для описания максимальной годовой снеговой нагрузки используют законы распределения Гумбеля
P(q |
|
|
q |
c1 |
|
, |
c1 |
) exp exp |
|
|
|||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
хотя этот закон допускает вероятность отрицательных значений qc1.
Коэффициенты и имеют различные значения для разных местностей. Например, для Москвы = 931 Н/м2, = 365 Н/м2.
Для определения максимально допустимой снеговой нагрузки на сооружение, рассчитанное на n лет, вероятность не превышения его значения qcn:
P qcn Pn qc1 .
Или вероятность превышения величины qcn за n лет
Q 1 Pn qc1
P qc1 n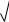 1 Q .
1 Q .
Величину qc1, соответствующую заданному числу лет n и допустимой вероятности Q, легко определить графически по кривой интегрального закона распределения P qcn .
Окончательно получим
|
|
|
|
|
q |
c1 |
|
|
|
|
q |
c1 |
|
|
|
|
|
|
n |
q |
c1 |
|
, |
||
|
P(q |
cn |
) exp |
n exp |
|
|
exp |
|
exp |
|
lnn |
|
exp |
exp |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где n |
lnn. |
|
|
|
|
|
|
|
|
|
|
|
за n |
|
|
|
|
|
|
|
|
|
|||
|
Т.о., |
переход от максимума за |
год |
к |
максимуму |
лет |
(при |
распределении |
|||||||||||||||||
Гумбеля) приводит к поступательному смещению кривой P(qc1) вдоль ОХ вправо на величину lnn . Также смещается и p(qc1).
Тогда можно записать
qcn qc1 lnn ,
но дисперсия при этом не изменяется D(qcn)=D(qc1).
Если рассматривать снеговую нагрузку как случайный стационарный процесс, то его можно задать следующим образом:
Так для г. Волгограда – аппроксимация функции м.о. высоты снегового покрова:
h(t) h0 A0 cos 2 t/T ,
где h0 = 4,3 см – среднее значение; А0 = 4,2 см – амплитуда;
Т = 180 дней – период математического ожидания.
Корреляционная функция случайного процесса h( ) аппроксимируется функцией
Kh ( ) De T ,
где D=D(h)=55,67 см2 – дисперсия высоты снегового покрова;= 0.04 день-1 – параметр функции.
11.2.2. Ветровая нагрузка
Нормативное значение ветрового давления
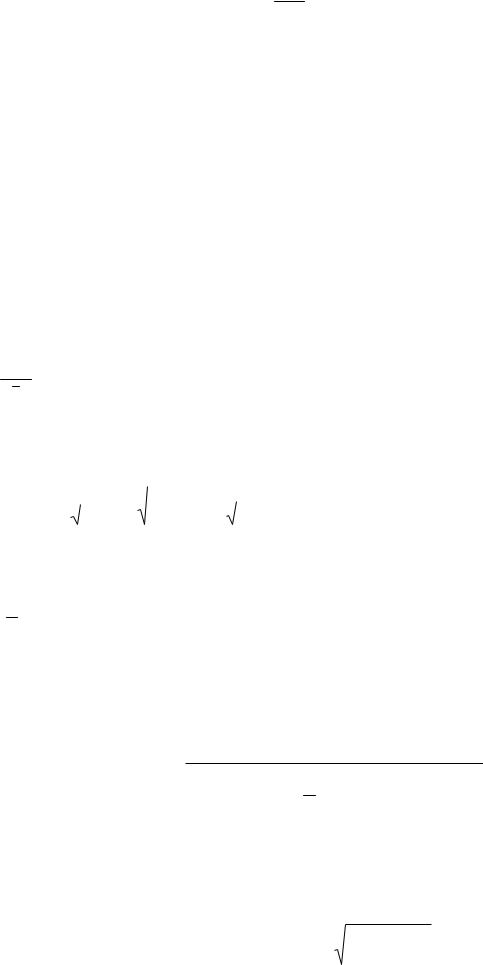
w0 V 2 , 2
где - плотность воздуха ( =f(p,t) const, p – давление, t – температура), V – скорость ветра.
Скорость ветра представляет собой случайную функцию времени, являющуюся пространственным вектором с координатами Vx(t), Vy(t), Vz(t). Распределение горизонтальных составляющих скорости ветра Vx и Vy определяет розу ветров. Обычно статистическое наблюдение ведут за скоростями ветра. В общем случае переход от статистического распределения скоростей ветра к распределению ветрового давления сложен, но переход может быть осуществлен приближенно.
В качестве функции распределения скоростей ветра w используют распределение Вейбулла
P(w) 1 exp( cwb ), c 0, b 0, 0 w
11.2.3. Постоянные нагрузки
Постоянные нагрузки — постоянные во времени случайные величины. Как правило, постоянные нагрузки обладают небольшой изменчивостью, порядка 0,1, (т. е.
V x x 0.1) и могут с достаточной точностью считаться подчиняющимися нормальным x
законам распределения. Если все нагрузки распределены по одному и тому же закону, то математическое ожидание их суммы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q Q1 |
Q2 |
... Qn . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Коэффициент вариации (изменчивости) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D Qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
2 |
... V Qn |
2 |
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
D Q |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
Qn |
|||||||||||||||||||||||||||||||||
|
|
|
V Q |
|
|
i 1 |
|
|
|
|
Q1 |
Q1 |
V Q2 |
Q2 |
|
|
, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1 Q2 |
... Qn |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
D Qi |
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
2 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
V |
|
Qi |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
V Qi , Qi — коэффициент вариации и математическое ожидание i-ой случайной нагрузки
Qi .
Формулы справедливы для корреляционно не связанных нагрузок.
В случае, когда отдельные независимые нагрузки по-разному приложены к конструкции и усилие в рассчитываемом элементе (например, колонне) выражается
n
линейной функцией N iQi , тогда коэффициент вариации случайного усилия N :
i 1
V N 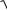
 V Q1 2 c12 V Q2 2 c22 ... V Qn 2 cn2 ,
V Q1 2 c12 V Q2 2 c22 ... V Qn 2 cn2 ,
где с |
iQi |
. |
||
|
||||
i |
n |
|||
|
i |
|
|
|
|
Qi |
|||
|
i 1 |
|||
Например, для колонны, если Qi — это распределенная нагрузка (кН/м2), то i —
это грузовая площадь i нагрузки, м2.
Приведенный (средний) коэффициент перегрузки:
n
f |
1 V N 1 |
V Qi 2 ci2 , |
|
|
i 1 |

где — характеристика безопасности
S1
S V S ,
где S — случайная величина резерва прочности.
Расчетное усилие:
Nрасч N N N 1 V N .
Приняв V Q |
fi 1 |
|
, где |
fi |
— коэффициент перегрузки отдельных нагрузок, |
||||
|
|||||||||
i |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
fi |
1 2 ; |
|
|
|
|
f |
|
1 |
ci2 |
|||
i 1
11.3.Превышение нагрузкой заданного уровня
Вбольшинстве случаев нагрузки, действующие на строительные конструкции, представляют собой случайные функции Q(t). Случайная функция Q(t) характеризуется
математическим ожиданием Q(t) (детерминированная функция аргумента t) и корреляционной функцией Kx(t1,t2) (см (67)).
Обычно нагрузка Q(t) — стационарный (или квазистационарный) случайный процесс и случайная функция.
Вернемся к формуле временной плотности вероятности выброса за уровень а для случайного стационарного процесса, т. е. когда случайная функция X(t) независима со своей
скоростью изменения V(t) dX(t) и тогда случайные функции X(t) и V(t) можно заменить dt
случайными величинами X и V с плотностями распределения PQ (q) иPV (v).
q(a) Px (a) PV (v)vdv
0
Применительно к перегрузкам, т. е. превышению нагрузки Q(t) или комбинации нескольких нагрузок некоторого допустимого уровня нагрузки а, запишем:
u(a) PQ (a) 0 PV (v)vdv,
где u(a) назовем интенсивностью отказов конструкции, считая отказом превышение нагрузкой Q(t) допускаемого для данной конструкции значения;
PQ (а) и PV (v) — плотности распределения Q(t) с аргументом а и V(t).
Величина, обратная интенсивности отказов, — период отказа, т. е. средняя продолжительность интервала между соседними выбросами (отказами).
(а) 1 u(a)
В большинстве случаев соседние отказы могут считаться независимыми случайными событиями, т. е. период отказа Q(а) значительно превышает интервал времени t2 - t1, в течение которого корреляционная функция KQ (t1,t2 ) 0 и к ним (отказам) можно применять
формулу вероятности непоявления редких событий
Pt |
exp |
|
t |
|
, |
u(a)dt |
|
||||
|
|
|
0 |
|
|
где Pt — вероятность того, что в течение времени t нагрузка Q(t) ни разу не превысит значение а.

Функция Pt представляет собой интегральную функцию распределения максимума
Q(t) за время t. Тогда надежность конструкции при заданном сроке t:
N PQ (a)Pt |
PQ |
|
t |
|
|
(a)exp u(a)dt |
|
, |
|||
|
|
|
0 |
|
|
где PQ (а) — интегральная функция распределения случайной нагрузки Q(t).
Связь между надежностью и интенсивностью отказов:
u(a) 1 dN d (ln N).
N dt dt
ЛИТЕРАТУРА
1.Арнольд В.И. Теория катастроф. – М.: Физматгиз, 1990.-126 с.
2.Аугусти Г., Баратта А., Кашиати Ф. Вероятностные модели в строительном проектировании. М.: Стройиздат, 1988.-584 с.
3.Барзилович Е. Ю., Беляев Ю. К. и др. Вопросы математической теории надежности. - М.: Радио и связь, 1983.-376с.
4.Барлоу Р., Прошан Ф. Математическая теория надежности и испытания на безотказность. /Пер. с англ. - М.: Советское радио, 1969.-488 с.
5.Барлоу Р., Прошан Ф. Статистическая теория надежности и испытания на безотказность. /Пер. с англ. - М.: Наука, 1984.-328с.
6.Болотин В. В. Методы теории вероятностей и теории надежности в расчетах сооружений. - 2-е изд., перераб. и доп. -М.: Стройиздат, 1981.-351 с.
7.Болотин В.В. Применение методов теории вероятностей и теории надежности в расчетах сооружений. – М.: Стройиздат, 1971.-255с.
8.Болотин В.В. Статистические методы в строительной механике. – М.: Стройиздат, 1965.- 202с.
9.Вентцель Е.С. Теория вероятностей. – М.: Наука, 1989.
10.Волков С.Д. Статистическая теория прочности. – М.: Машгиз, 1960.-176 с.
11.Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер. – М.: Высш. школа, 1999.-479с .
12.Гнеденко Б.В. Вопросы математической теории надежности. – М.:, 1983.
13.Гнеденко Б.В., Беляев Ю.К., Соловьев А.Л. Математические методы в теории надежности. – М.: Наука, 1965.-524 с.
14.Капур К., Ламберсон Л. Надежность и проектирование систем. – М.: Мир, 1980.-604 с.
15.Кудзис А.П. Оценка надежности железобетонных конструкций. – Вильнюс: Моклас, 1985.-155 с.
16.Ломакин В.А. Статические задачи механики твердых деформируемых тел. М., «Наука», 1970.
17.Лужин О.В. Вероятностные методы расчета сооружений. – М.: МИСИ им. Куйбышева, 1983.-122 с.
18.Райзер В.Д. Методы теории надежности в задачах нормирования расчетных параметров строительных конструкций. – М.: Стройиздат, 1986.-192 с.
19.Райзер В.Д. Расчет и нормирование надежности строительных конструкций. М.: Стройиздат, 1995.-348 с.
20.Райзер В.Д. Теория надежности в строительном проектировании:– М.: Изд-во АСВ, 1998.-304 с.
21.Ржаницын А.Р. Теория расчета строительных конструкций на надежность. -М.: Стройиздат, 1978.-239 с.
22.Саульев В.К. Статистическое моделирование: Метод Монте-Карло. – М.: МАИ, 1974.-67 с.
23.Свешников А.А. Прикладные методы теории случайных функций. – М.: Наука, 1968.- 463 с.
24.Синицын А.П. Расчет конструкций на основе теории риска. – М.: Стройиздат, 1985.-304 с.
25.Тимашев С.А. Надежность больших механических систем. – М.: 1981.
26.Тихонов В.И. Выбросы случайных процессов. – М.: , 1970.
27.Хан Г., Шапиро С. Статистические модели в инженерных задачах. – М.: Мир, 1969.-396 с.
28.Руководство по расчету зданий и сооружений на действие ветра. – М.: Стройиздат, 1978
29.СНиП 2.01.07-85* Нагрузки и воздействия

Леонид Павлович Бех
НАДЕЖНОСТЬ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
Учебно-методическое пособие по подготовке к занятиям по дисциплине
«Вероятностные методы строительной механики и теория надежности строительных конструкций»
для обучающихся по направлению подготовки 08.05.01 Строительство уникальных зданий и сооружений,
специализация Строительство высотных и большепролетных зданий и сооружений
Федеральное государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный архитектурно-строительный университет» 603950, Нижний Новгород, Ильинская, 65.
http://www.nngasu.ru, srec@nngasu.ru
