5684

В случае стационарного с.п. X(t) и Y(t) - независимые с.ф. и (при том V(t) d X(t) и dt

известна автокорреляционная функция для X(t) - KX( )), следовательно, p(x,V)=px(x) pV(V),

где p(x,V) - совместная плотность распределения X(t) и Y(t); px(x) и pV(V) - соответственно плотности распределения X(t) и Y(t).

Тогда временная плотность вероятности выброса:

q(a) px(a)pV (V)VdV px(a) pV (V)VdV ,

0 0

где pV (V)VdV V - м.о. положительной скорости V(t).

0

Для нормального распределения X(t):

распределение скорости V(t) будет также нормальным и независимым от распределения X(t):

Чем больше уровень а, тем меньше q(a). При очень малом значении q(a) выбросы можно рассматривать как редкие события, т.е. как независимые с.в.

Если число выбросов в течение времени t подчиняется закону Пуассона, тогда вероятность того, что за время T не произойдет ни одного выброса при условии, что X(t) – стационарная функция

Pt=exp[-q(a)T]

Это функция надежности.

В случае нестационарной функции

6. ПРИБЛИЖЕННЫЕ МЕТОДЫ НАХОЖДЕНИЯ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ С.В.

6.1. Метод Монте-Карло (метод рандомизации)

Есть система двух с.в. X и Y и p(x,y) – совместная плотность их распределения. Данный метод позволяет найти плотность распределения p(U), где U=U(X,Y).

Для одномерной с.в. Х, где р(х) – плотность ее распределения, можно найти p(U), причем U есть функция от X:

U=U(X)).

Суть метода в том, что аргументам X и Y даются случайные значения, распределенные согласно p(x,y). Случайные числа для значений аргументов можно брать по таблицам (есть таблицы для равномерного, нормального распределений, распределения Пирсона и т.д.) или определять на ЭВМ по специальной программе. Каждой случайной точке (xi,yj) соответствует определенное значение функции U(xi,yj). После реализации достаточно большого количества значений с.в. U их можно сгруппировать по интервалам n <U<(n+1) и построить ступенчатую аппроксимацию искомой кривой распределения p(U). Метод эффективен при использовании ЭВМ и при разрывности функции U(X,Y) (или при различном ее аналитическом описании в различных областях плоскости XOY).

Если есть функция двух с.в. U=U(X,Y) и p(x,y) – совместная плотность распределения X и Y, то

6.2.Метод статистических испытаний

Производится достаточно большое число статистических испытаний по схеме Бернулли, т.е. на каждом испытании генерируются случайные реализации всех исходных величин. Далее, например, если необходимо определить вероятность отказа системы, то испытания проводятся n раз, и каждый раз проверяется условие наступления отказа (например, Q>R, где Q – фактическая нагрузка на систему, R – прочность системы). Затем частота появления отказа: P*(A)=m/n, где m – количество отказов. При n -

P*(A) P(A),

где P(A) – вероятность наступления отказа, являющаяся достоверной величиной.

В данном методе необходимо оценить погрешность определения P*(A) при определенном количестве испытаний n или оценить количество испытаний n, необходимое для достижения частотой наступления отказа P*(A) достаточной достоверности.

7. ВЕРОЯТНОСТЬ РЕДКИХ СОБЫТИЙ (ПОЯВЛЕНИЕ СЛУЧАЙНОГО СОБЫТИЯ A ЗА ВРЕМЯ T)

Пусть некоторое событие A появляется случайно, причем корреляционная связь между вероятностями соседних по времени событий практически отсутствует, т.е. на срок возникновения последующего события не влияют сроки появления предыдущих. Наблюдениями в течение очень большого промежутка времени можно установить среднюю

частоту появления события A, т.е. число событий, образующееся в среднем за единицу времени. U=n/T, где n - число событий, появившихся за большой промежуток времени T.

Тогда вероятность появления события A хотя бы один раз за время t: 1- Pt = 1- e-ut,

где Pt - вероятность не появления события A за время t.

Если средняя частота появления события A - u переменна во времени (т.е. u=u(t)), то

есть функция надежности, представляющая собой вероятность непоявления события A в течение времени t ни разу.

При постоянной U(t)=const:

Pt=e-ut .

8.ПРОСТЕЙШИЕ МОДЕЛИ НАДЕЖНОСТИ

8.1.Последовательное соединение элементов

При последовательном соединении элементов разрушение происходит по наиболее слабому из них. Последовательным соединением элементов может быть названо также любое их соединение, образующее статически определимую систему. (Прочность – случайна, – напряжение в стержне от фактической определенной нагрузки).

Интегральный закон распределения прочности i-того элемента системы – Pi( ) (т.е. вероятность того, что прочность элемента будет находиться на интервале (- , ), т.е. это вероятность разрушения). Вероятность неразрушения равна 1-Pi( ) для i-того элемента. Аналогично для всей системы ее вероятность не разрушения 1-Pc( ), где Pс( ) – интегральное распределение прочности всей системы, состоящей из n последовательно соединенных элементов. Причем

n

1 Pc ( ) 1 Pi ( )

i 1

Предполагается, что прочность каждого элемента является независимой с.в. Если все элементы имеют одинаковые распределения своей прочности, выраженной через

внешнюю нагрузку (Pi( )=P1( ), i =1,2,…,n), то вероятность не разрушения

1 - Pc( ) = [1 - P1( )]n ,

где P1( ) – интегральное распределение прочности каждого элемента.

Распределение плотности вероятности разрушения системы: pc( )=n[1-P1( )]n-1 p1( ) ,

где p1( ) – плотность распределения прочности каждого элемента.

Если прочность элементов подчиняется распределению Вейбулла (54.4)

P1( ) = 1- exp(-c b) ,

то подставив (95.8) в (93.8) получим (вероятность разрушения системы)

который для случайной величины прочности системы Rc в b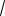n раз меньше, чем для случайной величины прочности элемента R1. Следовательно, в этом отношении изменяются (при переходе от одного элемента к системе последовательно соединенных элементов) и математическое ожидание и стандарт прочности

Если стержни системы сделаны из одного материала, но имеют различные поперечные сечения, то формула вероятности неразрушения системы:

Здесь F – внешняя нагрузка;

i – напряжение, вызываемое усилием F Ni1 в i-том стержне;

Ni1 - усилие в i-том элементе от внешней нагрузки F=1; Ai – площадь сечения i-того стержня.

В случае, когда прочность материала подчиняется распределению Вейбулла (54.4), вероятность неразрушения системы (подставим (95.8) в (98.8)):

Тогда м.о. и стандарт прочности системы:

8.2. Параллельное соединение элементов

Считаем элементы идеально хрупкими, модуль упругости и площадь сечения элементов одинаковыми и детерминированными. Известна функция распределения прочности Pr(R) и плотность распределения pr(R),

r

Pr (R) pr (R)dr; (0 R ).

0

Внешнее усилие N распределяется поровну между всеми n элементами, в которых напряжения не достигли предельных. При напряжении из строя выходит nPr( ) элементов (произведение общего количества стержней на вероятность выхода из строя одного) и м.о. воспринимаемого усилия:

N Fn1 Pr ( )

или т.к. E, то

N EF n1 Pr ( ) .

Уравнение (10.3) описывает диаграмму работы системы n параллельно соединяемых хрупких элементов, т.е. кривую состояний равновесия этой системы. Pr( ) – вероятность того, что прочность R будет меньше действующего напряжения , т.е. вероятность хрупкого разрушения стержня, F – площадь поперечного сечения каждого стержня. Рассмотрим зависимость напряжений от деформаций для хрупкого стержня = ( ).

Напряжения в стержне – с.в., т.к. его предел прочности R также с.в. М.о. действующего в стержне напряжения (из 102.8)

N /F n1 Pr ( )

и при n=1

E1 Pr ( E) ,

где - м.о. напряжения в стержне при деформации .

Т.к. функция ( ) разрывная, то возможны два события:

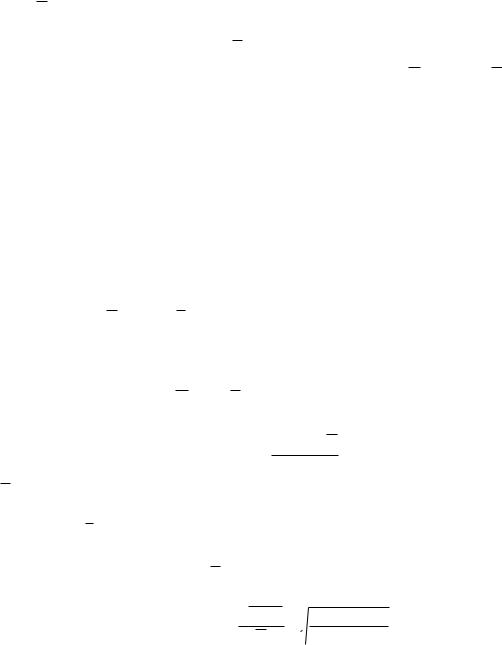
1)сопротивление равно E и вероятность этого 1 Pr ( E);

2)сопротивление равно 0 и вероятность этого Pr ( E), т.е. вероятность хрупкого разрушения

стержня и падения напряжения до нуля.

Согласно этому (и используя формулу определения м.о. для двух случайных событий X x1 p1 x2 p2 )

математическое ожидание:

E1 Pr ( E) .

Дисперсия (используя формулу для дисперсии D(X) p1 x1 X 2 p2 x2 X 2 ):

D( ) E1 Pr ( E) E E1 Pr ( E) 2 Pr ( E) E 1 Pr ( E) 2 2E2Pr ( E)1 Pr ( E) .

Подобным образом получаем корреляционную функцию

Данные характеристики относятся к одному хрупкому стержню. В случае n параллельно работающих стержней сопротивление системы (при одинаковой для всех стержней деформации) равно сумме сопротивлений составляющих:

n

N( ) F i ( ),

i 1

где N( ) и i ( ) - случайные несущая способность системы и действующее напряжение в i-

том стержне.

М.о. несущей способности

N( ) n F ( ) nF E1 Pr ( E) , что аналогично (102.8). Дисперсия несущей способности системы: D(N) n D( F) nF2D( ).

При этом предполагается, что прочности отдельных стержней – независимые с.в.

При нормальном распределении м.о. максимальной несущей способности системы:

N nFR(uV(R) 1)(0.5 Ф(u)),

где Ф(u) – интеграл вероятности Гаусса,

uE lim R ,

(R)

где R - ожидаемая прочность одного стержня (м.о.);(R) – стандарт этой прочности;

V(R) (R)/ R - коэффициент вариации прочности одного стержня. Дисперсия несущей способности системы:

D(N) nF2 R2 (uV(R) 1)2[0.5 Ф(u)][0.5 Ф(u)].

Коэффициент изменчивости несущей способности системы:

V(N) D(N) 0.5 Ф(u) .

N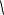 n(0.5 Ф(u))

9.МЕТОДЫ ОЦЕНКИ НАДЕЖНОСТИ КОНСТРУКЦИЙ

9.1.Развитие методов расчета в отечественных нормах

Необходимый уровень надежности обеспечивается не только расчетными требованиями норм проектирования, а зависит также от методов расчета, принятой конструктивной схемы, вида соединений конструктивных элементов, правил конструирования, плана контрольных испытаний и условий приемки при изготовлении и монтаже.

Изначально до середины 30-х годов прошлого века применялся метод допускаемых напряжений. Он заключался в том, что для любого волокна конструкции должно было выполняться условие

k S Sдоп,

где Sдоп - допускаемое напряжение; S - напряжение в волокне, определяемое методами строительной механики; k - коэффициент запаса.

В этом методе коэффициент запаса для всех конструкций из данного материала был одинаков, что не отвечало фактической работе таких комплексных материалов, какими являются железобетон и каменная кладка, компоненты которых имеют различные механические характеристики и в соответствии с этим в различной степени и с различной быстротой исчерпывают свою несущую способность. Кроме того, работа строительных материалов в конструкциях рассматривалась лишь в упругой стадии, т.е. не учитывались пластические свойства материалов изменчивость нагрузок и сопротивлений материалов. Поэтому метод допускаемых напряжений модифицировался в метод разрушающих нагрузок.

Расчетное условие этого метода в общем виде k Fн < Rн,

где k - коэффициент запаса, зависящий от соотношения нагрузок; Fн - нормативное значение нагрузки;

Rн - нормативное значение несущей способности (среднее значение прочности бетона или так называемая гарантируемая прочность стали).

Стала учитываться пластическая работа материала для определенных схем разрушения. Введение в середине 50-х годов ХХ века метода предельных состояний позволило

учесть специфику работы разных конструкций и фактическую изменчивость нагрузок и механических свойств строительных материалов и т.д., т.е. позволило достичь определенного выравнивания надежности отдельных элементов конструкции, составляющих единое целое.

Этот метод опирается на статистическое изучение значений нагрузок, механических свойств материалов и условий работы конструкций и материалов. Общее условие непревышения предельного состояния может быть представлено в виде

(Fp,Rp, n, a, c,с ) 0.

Здесь Fp - расчетное значение нагрузки;

Fp,=Fн f,

где f - коэффициент надежности по нагрузке; Fн - нормативное значение нагрузки.

Rp - расчетное значение сопротивления материала;

Rp=Rн/ m;

Rн - нормативное значение сопротивления материала;m - коэффициент надежности по материалу;

n - коэффициент надежности по ответственности конструкции;c - коэффициент условий работы;

a - коэффициент точности;

с - постоянные, включающие предварительно выбранные расчетные ограничения, задаваемые для некоторых видов предельных состояний (по прогибам, раскрытию трещин и т.п.).

Условие (1.10) определяет границу области допустимых состояний конструкции. Входящие в это условие факторы можно условно разделить на две группы. Первая группа факторов зависит от свойств самой конструкции, вторая от внешних воздействий. Это разделение возможно из-за отсутствия в большинстве случаев функциональных и корреляционных связей. Тогда условие (1.10) можно представить в виде:

n q (Fp , a , c ) r (Rp )

n (Fp ,Rp , a , c ) c

с - предельное значение нормируемых параметров (прогиба, угла поворота, раскрытия трещин).

Условие непревышения границы области допустимых состояний конструкций может определяться как

R-F>0,

где с.в. R – обобщенная прочность конструкции; F – обобщенная нагрузка,

или иначе

S = R-F,

где F – наибольшее значение усилия (или напряжения) в конструкции, выраженное через внешнюю нагрузку (т.е. задача определения напряженного состояния предполагается решенной);

R – несущая способность, выраженная в тех же единицах, и отвечающая предельному состоянию конструкции по прочности (предел текучести, предел прочности и т.д.);

S – резерв прочности.

9.2. Резерв прочности

Вероятность разрушения конструкции:

0

Q ps (S)dS Ps (0)

где ps(S) – плотность распределения резерва прочности.

Ps(0) – значение функции распределения резерва прочности при S=0 (вероятность того, что S 0, т.е. разрушения).

Плотность распределения резерва прочности при взаимонезависимости R и F:

ps (S) pr (S F)pf (F)dF ,

где pr(R) – плотность распределения несущей способности; pr(S+F) – та же функция, но с аргументом S+F;

pf(F) - плотность распределения внешнего усилия.

При взаимонезависимости R и F

p(S F,F) pr (S F)pf (F).

Эквивалентная формула

ps (S) pr (R)pf (R S)dR ,

где pf(R-S) - плотность распределения усилия, но с аргументом (R-S).

В случае, когда R и F зависимы, (5.10) и (5 .10) соответственно запишутся в виде

pS (S) p(S F,F)dF

и

pS (S) p(R,R S)dR,

где p(R,F) – функция совместной плотности распределения R и F; p(S+F,F) и p(R,R-S) – то же, но с аргументами S+F и R-S.

9.3. Характеристика безопасности

При любых законах распределения с.в. R и F м.о. и дисперсия резерва прочности S:

S R F ; (S) 2 (R) 2 (F) .

Для удобства вводят характеристику безопасности (при независимых R и F)

показывает число стандартов (S), укладывающихся в интервале от S до S S . Причем

1 ,

V(S)

где V(S) – коэффициент вариации (изменчивости) с.в. S (резерва прочности). Можно записать и так

0 S .

(S)

Для функции нормального распределения (см. 46.4) S вероятность разрушения:

где Ф( ) – интеграл вероятности Гаусса (47.4) с аргументом .

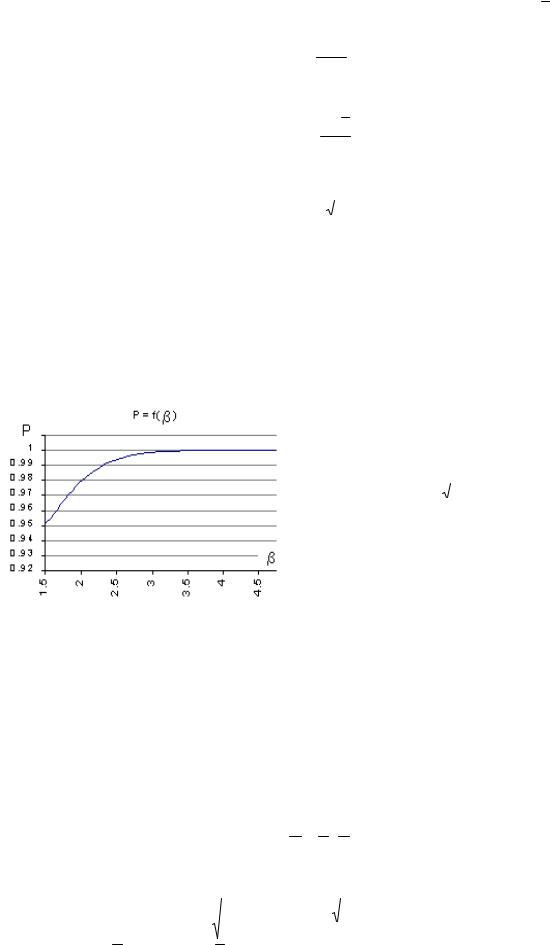
В таблице и на графике приведены зависимости характеристики безопасности от вероятности разрушения Q и неразрушения P.

Определять Q по (12.10) при больших затруднительно, поэтому используется асимптотическая формула

9.4. Коэффициент запаса

Иногда вместо резерва прочности вводят случайный коэффициент запаса

K=R/F .

здесь K, R, F – случайные величины.

Тогда вероятность разрушения

Q Q(K 1) PK (1) ,

где Pk(1) – функция распределения коэффициента запаса при аргументе K=1. Вероятность неразрушения

P=P(K>1).

М.о. коэффициента запаса (коэффициент детерминированный)

где V(F) (F)/F , V(R) (R)/R - коэффициенты вариации усилия и несущей способности.

Введение значений V(F) и V(R) имеет то преимущество, что они могут быть сравнительно легко оценены с достаточной точностью даже при отсутствии полных статистических данных относительно с.в. R и F. Кроме того, при изменении значения нагрузки, например, в результате увеличения площади, с которой она собирается, равно как при изменении прочности несущих элементов, например, вследствие увеличения размеров поперечных сечений, коэффициенты вариации

где V(K) (K)/K - коэффициент вариации коэффициента запаса. Приближенно

Можно вывести приближенную формулу, связывающую характеристику безопасности и коэффициент запаса

K 1 V 2 (R) V 2 (F) .

Выражение используется при небольших значениях V(R) и V(F), иначе

K 1 2V2 (R) 2V2 (F) 4V 2(R)V 2(F) .

1 2V2 (R)

В большинстве случаев корреляционная связь между нагрузкой и прочностью отсутствует или мала. Положительная корреляционная связь нагрузки с прочностью имеет место, когда для более прочных элементов с бо льшей вероятностью можно ожидать относительно бо льших нагрузок. Отчасти это относится к статически неопределимым конструкциям, в которых бо льшую прочность отдельных элементов можно считать связанной с их большей жесткостью, а, следовательно, и с бо льшими воспринимаемыми усилиями. Пример отрицательной корреляционной связи – ослабленное отверстием сечение более прочно, т.е. сечение меньше, а прочность больше.

Если удается оценить корреляционную связь R с F с помощью корреляционного момента K(R,F), то характеристика безопасности

где V(R,F) K(R,F) .

R F

Здесь K(R,F) запишется в виде

K 1 2V 2(R,F) 2 V2 (F) 2V2 (R,F) V2 (R) 4 V 2(R)V2 (F) V4 (R,F) .

1 2V 2(R)

10.СТАТИСТИЧЕСКИЙ ХАРАКТЕР ПРОЧНОСТИ

10.1.Начальная прочность материалов в строительных нормах

Вдействующих документах нормативные значения не совпадают с м.о. и сдвинуты по отношению к среднему значению.

При коэффициенте изменчивости прочности менее 0,06-0,08 применяется нормальный закон распределения (т.е. не учитываются моменты высших порядков – асимметрия и эксцесс). Более всего это относится к стали, для бетона, каменной кладки, древесины и других материалов с коэффициентом изменчивости 0,15-0,25 и более корректнее использовать более точные законы распределения, учитывающие асимметрию и эксцесс. Например, функция распределения, полученная из распределения Пирсона III типа:

Rn M(R) (R),

где M(R) — математическое ожидание предела текучести или временного сопротивления;

(R) — среднеквадратическое отклонение предела текучести или временного сопротивления.

1 n

M(R) Ri ; n i 1

(или по (19.3)

n

M(R) Ri pi ,

i 1