
книги / Электродинамика сплошных сред
..pdf
термопары поддерживают при постоянной температуре, другой помещают в объем, температуру которого хотят измерить. Между концами термопары ЭДС измеряется чувствительным вольтметром. Возможно измерение температур до сотых долей градусов. Термопары также используются в качестве маломощных источников тока, например, в полевых условиях.
1.5.4. Термогальваномагнитные явления
Термогальваномагнитные явления возникают при протекании тока при одновременном наличии электрического и магнитного полей и градиента температуры. В слабом магнитном поле H для изотропного проводника получается следующее выражение для напряженности электрического поля:
E = |
j |
+ αOT + RH [H × j] + N[H × OT ]. |
(1.120) |
σ |
Здесь RH – коэффициент Холла, описывающий эффект Холла. Слагаемое N[H × OT ] описывает эффект Нернста – влияние магнитного поля на термоэлектродвижущую силу.
Следующее выражение
q − ϕj = αT j − æ OT + NT [H × j] + L[H × OT ]. |
(1.121) |
Здесь слагаемое NT [H × j] описывает эффект Эттингсхаузена – влияние магнитного поля на эффект Пельтье, а слагаемое L[H × OT ] – эффект Ледюка-Риги – влияние магнитного поля на теплопроводность. Здесь N и L – константы.
Выражение для количества теплоты будет выглядеть следующим образом:
Q = div (æ OT ) + |
j2 |
− T j · Oα + |
1 d |
(σNT 2)[j × H] · OT. |
(1.122) |
||
|
|
|
|
||||
σ |
σT dT |
||||||
Здесь последнее слагаемое описывает изменение эффекта Томпсона при наличии магнитного поля.
61
1.6.Магнетики
1.6.1. Намагничивание
Если магнитное поле существует не в вакууме, а в какой-либо среде, то оно изменится. Различные вещества во внешнем магнитном поле µ0H намагничиваются, т.е. сами становятся источниками магнитного поля Bm. Результирующее поле B = µ0H + Bm , µ0H. Таким образом, магнетики – это вещества, способные намагничиваться.
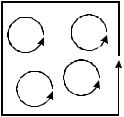
Механизм намагничивания состоит в том, что во всех веществах существуют мельчайшие молекулярные электрические токи, которые замыкаются в пределах атома (гипотеза Ампера, рис. 1.18). При намагничивании магнетика расположение молекулярных токов упорядочивается и их суммарное действие становится отличным от нуля.
Действие замкнутого тока определяется магнитным моментом pm = IS n, где I – сила молекулярного тока, S – площадь, обтекаемая током, n – единичная нормаль к поверхности витка с током. Суммарное действие, описывающее магнитное состояние вещества, называется намагниченностью, M = P pm/4V, где 4V – физически малый объем, в котором суммируются все молекулярные токи.
J
Рис. 1.18
Напряженность магнитного поля в магнетике Hm равна напряженности внешнего магнитного поля в вакууме H (если убрать магнетик), т.е. она не изменяется, Hm = H. Молекулярные токи суммарно создадут в намагниченном магнетике поверхностный ток J (см. рис. 1.18), при этом напряженность поля поверхностного тока HJ = M, а индукция в магнетике BJ = µ0M. Полная магнитная индукция в магнетике
B = µ0H + BJ = µ0H + µ0M. |
(1.123) |
62
В изотропных магнетиках связь между намагниченностью и напряженностью M = χmH определяется магнитной восприимчивостью данного вещества χm, которая зависит от вида магнетика и его состояния (температуры и т.д.). Тогда связь между магнитной индукцией и напряженностью магнитного поля будет описываться таким соотношением:
B = µµ0H. |
(1.124) |
Здесь µ = 1 + χm – магнитная проницаемость вещества, которая показывает, во сколько раз магнитная индукция, т.е. средняя плотность магнитного потока в магнетике, больше плотности магнитного потока от магнитного поля без магнетика. В анизотропных средах величины χm и µ являются тензорами.
1.6.2. Природа молекулярных токов
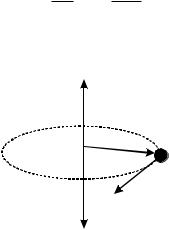
Электроны в атомах обращаются вокруг ядра по круговым орбитам. Такое движение электронов представляет собой замкнутый электрический ток (рис. 1.19). При этом у них есть механический момент, так как электроны обладают массой, и |Lw| = m e¯ωr2 = 2m e¯νS , где ω = 2πν – угловая скорость электрона. Помимо механического, еще существует орбитальный магнитный момент |pm| = e¯νS , где e¯ν = I – сила тока. Направления pm и L – противоположны. Гиромагнитное соотношение – отношение этих моментов
= pm = − e¯
Lw 2me
не зависит от ν и S и определяется константами.
pm
r
V
L
Рис. 1.19
63
Если на движущийся электрон воздействовать внешним магнитным полем H, то согласно теореме Лармора на первоначальное движение электрона будет наложено добавочное равномерное вращение вокруг направления внешнего магнитного поля. Угловая скорость прецессии
Ω = e¯µ0H .
2me
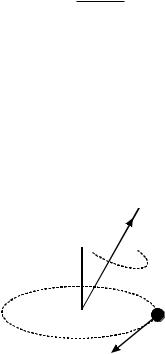
Таким образом, внешнее магнитное поле не вызывает переориентировку электронных орбит, а вызывает только их прецессию (рис. 1.20), хотя под действием соударений с соседними атомами ориентация будет меняться так, чтобы векторы pm и H стали параллельными: pm H – и вещество намагнитилось.
H pm
pm 





V
Рис. 1.20
Рассмотрим два случая. Если железный цилиндр помещен внутрь соленоида с электрическим током, то под действием внешнего магнитного поля, которое генерирует соленоид, происходит намагничивание цилиндра и он начинает вращаться. В этом состоит магнито-механическое явление (Эйнштейн, Гааз), причем направление вращения цилиндра изменяется при изменении направления внешнего поля. Обратно, если начать вращать железный цилиндр, то он начинает намагничиваться – в этом состоит механо-магнитное явление (Барнетт). При вращении атомы, обладая моментом импульса, будут ориентироваться, при этом вещество намагничивается. Эти два явления доказывают, что молекулярные токи, обусловливающие намагниченность, обладают механическим моментом и намагничивание вещества обусловлено движущимися электронами.
64

1.6.3. Спин
Теоретически гиромагнитное соотношение должно выглядеть следующим образом: teor = − e¯/2m e¯, однако экспериментально установлено, что это соотношение должно быть в два раза больше exp − e¯/m e¯. Внутри атома, помимо орбитального движения электронов, имеется другой тип движения, приводящий к возникновению магнитного и механического моментов. Следовательно, самому электрону присущи моменты pme и Le, причем
|
|
= |
|pme| |
= |
− |
e¯ |
. |
e |
|Le| |
|
|||||
|
|
|
2m e¯ |
||||
Таким образом, электрон подобен заряженному телу, вращающемуся вокруг своей оси. Характеристикой этого вращения является спин электрона – собственный механический момент количества движения электрона Le.
Проекция спина на направление внешнего магнитного поля H принимает только два значения – положительное и отрицательное, т.е. направление спина квантуется:
LeH = ±1 h ,
2 2π
где h – постоянная Планка. Следовательно, квантуется и направление собственного магнитного момента электрона:
pmeH = LeH · e = ± |
h e¯ |
= ±µB, |
||
|
|
|
||
4π m e¯ |
||||
где µB – магнетон Бора.
Следовательно, магнетизм атомов обусловлен двумя причинами: движением электронов в атоме и магнетизмом самих электронов, которые являются источниками магнитного поля независимо от их движения внутри атомов. Таким образом, исходным источником магнитного поля всегда в том или ином виде является электрический ток. В любом веществе, так же как и вакууме, справедлива теорема Гаусса: линии вектора B везде остаются непрерывными:
I
B · dS = 0. |
(1.125) |
65

1.6.4. Диамагнетизм (µ < 1)
Диамагнетики – это вещества, которые не содержат постоянных атомных или молекулярных диполей (например, бензол). В этих веществах внешнее магнитное поле индуцирует в электронных облаках атомов круговые токи, что согласно правилу Ленца порождает противоположно направленное магнитное поле. В результате суммарное магнитное поле B будет меньше, чем в вакууме µ0H.
Найдем значение магнитной проницаемости диамагнетика. Рассмотрим движущийся электрон в атоме (рис. 1.21). При воздействии внешнего магнитного поля электрическое поле вдоль траектории электрона
I Z Z
E · dL = 2πrE = rot E · dS = − ∂tB · dS ≈ −πr2µ0∂t H,
следовательно,
E = −rµ0∂t H/2.
V 
 r
r 
 H 0
H 0
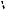 Iind
Iind 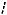
Рис. 1.21
Под действием электрического поля E электрон ускоряется до скорости V и будет вращаться с частотой ν по круговой траектории:
e¯E = me∂tV = r e¯µ0∂t H/2,
тогда
Z
V = ∂tVdt = r e¯µ0H = 2πνr.
2m e¯
66

Индуцированный ток
Iind = e¯ν = µ0 e¯2H .
4πm e¯
Тогда намагниченность системы из N атомов
M = NIindπr2 = χDH,
где магнитная восприимчивость диамагнетика
χD = −µ0N e¯2r2 .
4me
Связь магнитной индукции и напряженности в диамагнетике
B = (1 + χD)µ0H = µDµ0H,
где магнитная проницаемость диамагнетика
µD = (1 + χD) = 1 − |
µ0N e¯2r2 |
(1.126) |
4me . |
Описанный механизм возникновения противоположного магнитного поля эквивалентен ларморовой прецессии. Вследствие того что ларморову прецессию в магнитном поле испытывают все электроны любого атома, атомы всех веществ являются носителями диамагнитных свойств. Однако по сравнению с величинами магнетона Бора и дипольного момента ларморовский магнитный момент имеет незначительную величину.
Следует отметить, что в металлах возникает дополнительный диамагнитный эффект, связанный с электронами проводимости. Однако действие этого эффекта в три раза слабее, чем действие парамагнитного эффекта, поэтому он не наблюдается на опыте.
1.6.5. Парамагнетизм (µ > 1)
Парамагнетики – это вещества, способные сильно намагничиваться из-за того, что их атомы обладают постоянным магнитным дипольным моментом и спином. В отсутствие внешнего поля диполи ориентированы беспорядочно, поэтому суммарный магнитный момент,
67

H=0  H
H
M=0 M= pm
Рис. 1.22
P
или намагниченность, M = pm → 0. Под действием внешнего магнитного поля диполи стремятся выстроиться параллельно полю, pm H (рис. 1.22).
Чтобы получить выражение для парамагнитной проницаемости, воспользуемся теорией Ланжевена для диполей, проведя аналогичные выкладки, как и в теории диэлектриков Для этого примем ряд допущений, а именно: направление pm не квантуется; тепловое действие на намагничивание определяется статистикой Больцмана; температуры не низкие. Намагниченность парамагнетика, состоящего из N диполей, будет связана с напряженностью внешнего поля:
µ0 pmH , k T
где L – функция Ланжевена. Рассмотрим два случая.
При больших магнитных полях и малых температурах, когда выполняется условие pmH k T (случай, когда L(ξ) → 1), происходит полная поляризация парамагнетика и он становится насыщен:
M = N pm.
При малых магнитных полях и больших температурах, когда выполняется условие pmH k T (случай, когда L(ξ) → ξ/3), зависимость будет следующая (Кюри):
|
µ0N p2 |
|
|||
M = χPH = |
|
m |
H. |
(1.127) |
|
|
|
||||
|
3 k T |
|
|||
Таким образом, магнитная проницаемость парамагнетика |
|
||||
|
|
µ0N p2 |
|
||
µP = (1 + χP) = 1 + |
|
m |
. |
(1.128) |
|
|
|
||||
|
|
3 k T |
|
||
68
1.6.6. Ферромагнетизм (µ 1)
Ферромагнетики – это вещества, способные сильно намагничиваться из-за того, что их атомы обладают постоянным магнитным дипольным моментом и спином, при этом, в отличие от парамагнетиков, они сильно связаны между собой. Ферромагнетики обладают следующими свойствами:
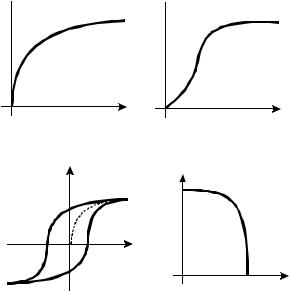
1)Имеют сложную нелинейную зависимость магнитной индукции от напряженности B(H) (рис. 1.23,а).
2)Зависимость намагниченности ферромагнетика M = B/µ0 − H имеет насыщение при больших H (рис. 1.23,б).
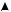 B
B 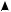 M
M
H H
а |
б |
|
B |
F |
|
BR |
||
|
H
H
TK T
в |
г |
Рис. 1.23
3)Все монокристаллические ферромагнетики анизотропны – у них есть направления легкого намагничивания.
4)Имеют гистерезис – зависимость индукции от предыдущих состояний намагничивания. При гистерезисе появляется остаточная индукция BR (рис. 1.23,в), которую можно удалить с помощью внешнего магнитного поля, значение которого определяется коэрцитивной силой HC , направив его противоположно исходному. Магнито-мягкие материалы обладают высоким значением магнитной проницаемости
µи малым значением коэрцитивной силы, их намагниченность мала.
69
Такие материалы применяются, например, в сердечниках трансформаторов. Магнито-твердые материалы обладают большим значением коэрцитивной силы и способны намагничиваться. Из этих материалов изготавливают, например, постоянные магниты.
5) Существует критическая температура Кюри ферромагнетиков TK, (рис. 1.23,г), при превышении которой ферромагнетик превращается в парамагнетик вследствие резкого повышения влияния теплового движения молекул. Для некоторых ферромагнитных материалов значение температуры Кюри следующее: для никеля TK = 360oC, для железа TK = 770oC, для кобальта TK = 1150oC.
Вейсс описал поведение ферромагнетика вблизи точки TK, введя дополнительное локальное магнитное поле HL в месте нахождения каждого диполя, которое порождается соседними связанными диполями. Это локальное поле прямо пропорционально намагниченности HL = λM. Подставим его в формулу Кюри (1.127) и получим
M = |
µ0N pm2 (H + HL) |
|||||
|
|
|
, |
|||
|
|
|
||||
|
|
|
|
3 k T |
||
|
M |
µ0N pm2 |
||||
χF = |
|
= |
|
. |
||
|
|
|||||
|
H |
3 k (T − TK) |
||||
Таким образом, температура Кюри пропорциональна мере связи λ магнитных диполей в ферромагнетике.
λµ0N p2 |
|
||||
TK = |
|
m |
. |
|
(1.129) |
3k |
|
||||
|
|
|
|
|
|
Тогда магнитная проницаемость ферромагнетика |
|
||||
µF = (1 + χF ) = 1 + |
µ0N pm2 |
(1.130) |
|||
|
. |
||||
|
|||||
|
|
3 k (T − TK) |
|
||
Представление о структуре ферромагнетиков было сформировано на основе следующих фактов:
1) У ферромагнетиков намагниченность можно повысить до достаточно большого значения насыщения действием относительно слабого внешнего магнитного поля.
70
