книги / Электродинамика сплошных сред

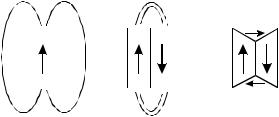
2)Для ферромагнетика и парамагнетика величины магнитных моментов pm имеют близкие значения (опыты Штерна и Герлаха). Следовательно, ферромагнетизм нельзя объяснить при помощи теории парамагнетизма.

3)В ферромагнетиках реальное гиромагнитное отношение равно удвоенному значению гиромагнитного отношения e для электронных орбит, полученному в теории, т.е. = 2 e. Поэтому намагничивание ферромагнетиков обусловливается очень сильной ориентировкой спинов, но не магнитных моментов атомов в целом.

Ферромагнетик разбивается на большое число малых, но макроскопических областей – доменов (гипотеза Вейсса). Размер домена порядка 10−6м. Каждый домен при T < TK намагничен до насыщения, но направления намагниченности в доменах различны, поэтому суммарная намагниченность стремится к нулю. Существование доменов в ферромагнетиках доказано в экспериментах. Сильная ориентировка спинов при самопроизвольном намагничивании вызывается силами обменного взаимодействия – это объясняется в рамках квантовой механики (Френкель, Гейзенберг).

Рис. 1.24

Причина возникновения доменов состоит в том, что ферромагнетик стремится уменьшить свою энергию (Ландау). В отсутствие внешнего магнитного поля магнитные силовые линии проходят внутри ферромагнетика, при этом линии становятся короче, что снижает энергию магнетика (рис. 1.24).

При воздействии внешнего поля происходит следующее (рис. 1.25). Энергия доменов становится разной – больше в тех доменах, где угол

71

между векторами магнитного поля H и намагниченности M более острый. Объем этих доменов становится больше вследствие смещения границ доменов. При дальнейшем увеличении поля энергетически невыгодные домены исчезают, при этом смещения границ становятся необратимы. Если еще увеличить поле, то происходит поворот магнитного момента внутри доменов. Последующее увеличение поля приведет к тому, что все векторы магнитных моментов установятся параллельно вектору внешнего магнитного поля. Происходит насыщение ферромагнетика.

Рис. 1.25

Смещение границ и поворот магнитного момента происходят с задержкой, отстают от изменения внешнего магнитного поля. Это приводит к появлению гистерезиса.

При возникновении самопроизвольного намагничивания (например, при снижении температуры ниже TK) ферромагнетик деформируется (например, сферическое ферромагнитное тело принимает эллиптическую форму). Это явление называется магнитострикцией, оно открыто Джоулем и используется в настоящее время, например, в излучателях приборов для ультразвукового исследования.

1.6.7. Плотность молекулярного тока

Напряженность магнитного поля всего тока можно определить как сумму напряженностей полей, создаваемых отдельными элементами:

где интегрирование должно быть распространено на весь объем тока, а r – расстояние рассматриваемой точки поля от элемента тока dV.

72

С помощью преобразований можно получить следующее выражение:

Внесем это выражение в (1.131) и, меняя порядок операций, получим

где выражение для векторного потенциала выглядит таким образом:

V

Магнитное поле атомов постоянно во времени и может быть сведено к полю постоянных замкнутых токов, распределенных внутри атома или молекулы с определенной плотностью jm = pm × r. Векторный потенциал такого тока [pm × r]/r3. Тогда выражение для векторного потенциала магнитного поля всех молекулярных токов, циркулирующих во всех элементах магнетика, будет следующим:

где im = rot sur f M – плотность поверхностных молекулярных токов, пропорциональная поверхностному ротору намагниченности. Тогда средняя плотность объемных молекулярных токов, связанная с намагниченностью среды, выглядит следующим образом:

73

1.6.8. Пондеромоторные силы в магнетиках

Механические силы, действующие на магнетики в магнитном поле, должны сводиться к силам, действующим на молекулярные токи. Сила, действующая на систему замкнутых токов, характеризуемую магнитным моментом pm, определяется как F1 = µ0O(pmHmic). Средняя сила будет определяться средней напряженностью микроскопического поля hHmici, которая равна вектору магнитной индукции B/µ0. Тогда средняя сила

F2 = O(pmB) = pmO · B + [pm × rot B].

Плотность пондеромоторных сил, испытываемых магнетиком, т.е. сила, действующая на единицу объема магнетика, будет равна сумме сил, действующих на отдельные молекулы, которые находятся в единице объема:

X X X

f = F2 = pmO · B + [pm × rot B] =

X X

h i

= pm O · B + pm × rot B .

Таким образом,

1.7.Электромагнитное поле в веществе

1.7.1. Система уравнений Максвелла

Изначально основные уравнения теории электромагнитного поля описывали величины, относящиеся к данной точке и данному моменту времени. Эти уравнения описывали электромагнитные процессы, происходящие в вакууме, предметом их рассмотрения служили как электрические заряды, движущиеся в вакууме, так и окружающее их электромагнитное поле.

74

Запишем эту систему уравнений Максвелла-Лоренца в несколько

В веществе – среде, построенной из атомов и молекул, уравнения Максвелла-Лоренца, содержащие характеристики поля, отнесенные к данной точке и данному моменту времени, теряют смысл. Действительно, в веществе все величины, в том числе и электромагнитное поле, весьма быстро изменяются от точки к точке и во времени. Например, напряженность электрического поля имеет сравнительно малое значение вне данного атома, становится весьма большой внутри него и вновь спадает за его переделами. Рост поля в миллионы раз и его последующее уменьшение происходят в масштабах порядка атомных размеров. Такое же изменение поля во времени в фиксированной точке происходит, например, из-за теплового движения атома за малые доли секунды. Поэтому, как и в других макроскопических процессах, происходящих в веществе, значение имеют лишь средние величины.

Усредним уравнения Максвелла-Лоренца по физически бесконечно малым объему V и промежутку времени τ:

При этом будем называть среднее значение напряженности электрического поля в среде hei напряженностью поля E = hei, а среднее значение напряженности магнитного поля в среде hhi магнитной индукцией B = µ0hhi – такие названия связаны исключительно с исторической традицией.

75

Полная средняя плотность заряда hρΣi определяется как сумма полного свободного заряда ρc и полного связанного заряда ρΣ в среде,

Средняя плотность тока hρΣUi = jΣ зарядов, движущихся в среде со скоростью U, равна сумме плотности тока проводимости j, определяемой по закону Ома, плотности тока смещения jd, определяемой выражением (1.79), и плотности молекулярных токов, определяемой выра-

Выражения в скобках представляют собой напряженность магнитного поля H = B/µ0 − M и поле электрического смещения D = P + ε0E.

Преобразуем выражение (1.144):

ε0 div E = ρc + ρd = ρc − div P,

откуда

div (P + ε0E) = ρc.

76

Окончательно, выполнив все подстановки, получаем систему урав-

Необходимо подчеркнуть, что в отличие от уравнений МаксвеллаЛоренца, являющихся одним из самых точных и универсальных законов природы, система уравнений Максвелла имеет ограниченную область применимости вследствие ограниченности действия уравнений связи. Эти уравнения неприменимы для анизотропных сред, где в уравнениях связи величины диэлектрической и магнитной проницаемости являются тензорами. Далее, линейное соотношение между намагниченностью и индукцией не выполняется для ферромагнетиков, и между поляризацией и напряженностью электрического поля – для сегнетоэлектриков. Также эти уравнения не описывают поведение сверхпроводников и сред, обнаруживающих временную или пространственную дисперсии.

Таким образом, нам еще понадобятся уравнения, описывающие электрические и магнитные свойства среды. Для поля распределения заряда запишем следующее:

0 – электрически нейтральная среда,

ρc =

ρ (r) – заряженная среда.

c

Для выражения электрического смещения

εε E – нормально диэлектрическая среда,

0

D =

D(E) – сегнетоэлектрическая.

77

Для выражения индукции магнитного поля

µµ H – диаили парамагнитная среда,

0

B =

B(H) – ферромагнитная.

Осталось дополнить систему Максвелла граничными условиями. На границе раздела двух проводящих сред с электропроводностью σ1 и σ2 нормальная компонента напряженности электрического поля терпит скачок, а тангенциальная – не изменяется:

Из этих условий вытекают граничные условия для плотности электрического тока

На границе раздела двух диэлектриков с диэлектрической проницаемостью ε1 и ε2 будут следующие условия для напряженности электрического поля:

На границе раздела двух магнетиков с магнитной проницаемостью µ1 и µ2 выполняются граничные условия для напряженности магнитного поля

и для магнитной индукции

1.7.2. Движение проводника в магнитном поле

Вначале рассмотрим покоящийся металлический проводник в виде ленты шириной a, по которому протекает электрический ток плотностью j в направлении оси OY (рис. 1.26). Если поместить ленту в однородное

78

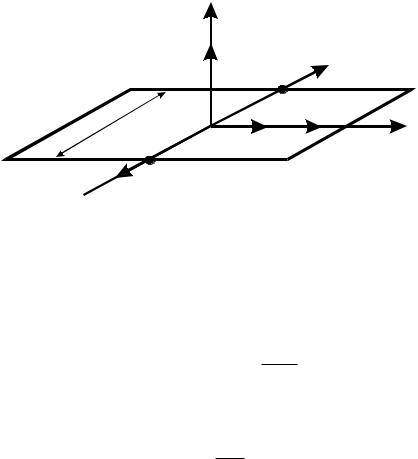
магнитное поле h, направленное по оси OZ, то электрические заряды, движением которых обусловливается ток, будут испытывать добавочную силу F = µ0 e¯[U × h], где U – средняя скорость носителей тока. Эта добавочная сила будет отклонять ток по направлению оси OX – струя электронов будет «бить» в передний край ленты и вызывать там накопление отрицательных зарядов. Этот процесс называется эффектом Холла, и он будет продолжаться до тех пор, пока результирующая сила поля накопившихся у правого края отрицательных зарядов и поля избытка положительных зарядов у левого не уравновесит силы F. Обозначая это уравновешивающее поле через E, получаем

e¯E = −F = −µ0 e¯[U × h].

X

Рис. 1.26

Поле E направлено по оси OX, при этом разность потенциалов между краями ленты

ja|h|

ϕA − ϕB = Exa = µ0Ua|h| = µ0 e¯N = RH jaµ0|h|.

Здесь введен коэффициент Холла,

Теперь рассмотрим металлический проводник, к которому не приложено сторонних ЭДС – то есть по нему не течет электрический ток.

79

Пусть он движется во внешнем магнитном поле h со скоростью V. Обозначим через UR скорость относительно проводника какого-либо электрона проводимости этого проводника. Полная скорость электрона будет равна Uf = V + UR. На электрон будет действовать сила Лоренца

F f = µ0 e¯[V × h] + µ0 e¯[UR × h] = F + FH.

Сила FH перпендикулярна скорости UR электрона относительно проводника, поэтому эта сила не будет изменять скорости UR, а будет лишь искривлять путь электрона в проводнике и приводить к эффекту Холла. Сила F = µ0 e¯[V × h] отлична от нуля только в движущихся проводниках, она не перпендикулярна UR, и поэтому может ускорять (или замедлять) движение электронов относительно проводника, то есть генерировать электрический ток. В этом состоит явление индукции токов при движении проводника в магнитном поле.

Выражение плотности пондеромоторных сил, полученное для неподвижных проводников (1.101), применимо также и к движущимся проводникам. Сумма сил, испытываемых в магнитном поле h всеми электронами проводимости, находящимися в единице объема проводника,

F− = µ0N e¯[V × h] + µ0N e¯[hURi × h],

где N – число электронов в единице объема, а hURi – средняя скорость электронов относительно проводника. Магнитное поле действует не только на электроны, но и на положительные ионы, движущиеся со скоростью V. Сумма сил, действующих на ионы, находящиеся в единице объема проводника,

F+ = −µ0N e¯[V × h].

Так как при условии нейтральности проводника суммарный заряд положительных ионов должен равняться с обратным знаком сумме N e¯ зарядов электронов, следовательно, равнодействующая всех сил, приложенных к единице объема проводника, может быть выражена как

Fs = F− + F+ = µ0N e¯[hURi × h].

Если по неподвижному проводнику течет электрический ток, направление которого не совпадает с направлением поля, то во внешнем

80