Наилучшие результаты прогнозирования методом экспоненциального сглаживания

Код	Квартал	Фактическое значение	Прогнозируемое значение	Отношение стандартной ошибки к среднему значению	alpha
y1	1/2005	83098	81561,3	0,268499	0,2
	2/2005	106481	169571,6
	3/2005	238814	218142,3
y2	1/2005	63636	64693,4	0,259429	0,2
	2/2005	85730	134700,4
	3/2005	186906	175173,8
y3	1/2005	3958	4249,84	0,130126	0,2
	2/2005	6161	6901,81
	3/2005	8593	7434,42
y4	1/2005	12950	13568,10	0,30844	0,2
	2/2005	14928	24277,83
	3/2005	37149	30345,18
y5	1/2005	2554	1142,08	0,424015	0,6
	2/2005	2216	4374,69
	3/2005	6166	6882,86
y6	1/2005	1428	-215,322	0,510646	0,2
	2/2005	2487	1220,687
	3/2005	3911	2901,314

Окончание таблицы 5.3.2

Код	Квартал	Фактическое значение	Прогнозируемое значение	Отношение стандартной ошибки к среднему значению	alpha
y7	1/2005	283	358,425	0,32	0,2
	2/2005	716	532,207
	3/2005	1118	778,259
y8	1/2005	673	543,879	0,2561	0,2
	2/2005	400	613,117
	3/2005	765	656,531
y9	1/2005	47586	32643,5	0,979917	0,2
	2/2005	10864	66747,1
	3/2005	52109	75904,5
y10	1/2005	48991	8613,54	0,798277	0,2
	2/2005	9633	38280,2
	3/2005	54554	38125,9
y11	1/2005	67	6133,17	19,51832	0,2
	2/2005	199	3947,58
	3/2005	444	4072,29
y12	1/2005	465	29843,7	26,0861	0,2
	2/2005	459	3791,2
	3/2005	1071	6416,1
y13	1/2005	139,6605042	121,089	0,313092	0,2
	2/2005	177,7646077	305,379
	3/2005	396,0431177	397,687
y14	1/2005	4,292436975	2,36924	0,415475	0,4
	2/2005	3,699499165	5,44379
	3/2005	10,22553897	6,71059

Результаты сглаживания и прогнозирования для коэффициента сглаживания = 0,2, при котором получены наиболее достоверные результаты прогнозированияy₁ и y₁₃ и для = 0,6, при котором получены наиболее достоверные результаты прогнозирования дляy₅, представлены на рис. 5.3.1. – 5.3.3.

Рис. 5.3.1. Прогнозируемое значение выручки (нетто) от продажи товаров, продукции, работ, услуг

Рис. 5.3.2. Прогнозируемое значение прибыли от продаж

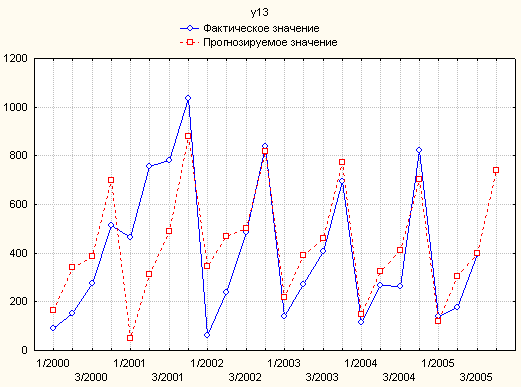
Рис. 5.3.3. Прогнозируемое значение дохода на одного работника

5.4. Прогнозирование методом авторегрессии и проинтегрированного скользящего среднего

Прогнозирование на ВДР, в которых наряду с общей тенденцией изменения переменных во времени, требуется учитывать и, так называемую, «сезонную» составляющую, весьма успешно проводится методом Бокса-Дженкинса [2], называемого АРПСС – авторегрессионным и проинтегрированным скользящим средним.

Общая модель, предложенная Боксом и Дженкинсом [2], включает как параметры авторегрессии, так и параметры скользящего среднего. Вводится три типа параметров модели: параметры авторегрессии (p), порядок разности (d), параметры скользящего среднего (q). В обозначениях Бокса и Дженкинса [2] модель записывается как АРПСС (p, d, q). Например, модель (0,1,2) содержит 0 (ноль) параметров авторегрессии (p) и два параметра скользящего среднего (q), которые вычисляются для ряда после взятия разности с лагом 1.

Мультипликативная сезонная АРПСС представляет естественное развитие и обобщение обычной модели АРПСС на ВДР, в которых имеется периодическая сезонная компонента. В дополнении к несезонным параметрам – общей тенденции изменения ВДР, в модель вводятся сезонные параметры для определения лага (устанавливаемого на этапе идентификации модели). Аналогично параметрам простой модели АРПСС, эти параметры называются: сезонная авторегрессия (ps), сезонная разность (ds) и сезонное скользящее среднее (qs). Таким образом, полная сезонная АРПСС может быть записана как АРПСС (p, d, q)(ps, ds, qs). Например, модель (0, 1, 2)(0, 1, 1) включает 0 регулярных параметров авторегрессии, 2 регулярных параметра скользящего среднего и 1 параметр сезонного скользящего среднего. Сезонный лаг, используемый для сезонных параметров, определяется на этапе анализа характеристик ИСД.

Для учета имеющейся авторегрессии требуется выделить элементы, которые последовательно зависят друг от друга. Такую зависимость можно выразить следующей математической зависимостью:

, (5.4.1)

где - константа (свободный член);

- параметры авторегрессии;

- случайное воздействие.

Можно заметить, что каждое наблюдение есть сумма случайной компоненты (случайного воздействия ) и линейной комбинации предыдущих наблюдений.

Результаты прогнозирования методом авторегрессии и проинтегрированного скользящего среднего представлены в таблицах 35 – 48 приложения 1.

Сводные результаты прогнозирования методом авторегрессии и проинтегрированного скользящего среднего при изменении интервала сезонности приведены в таблице 5.4.1.

По результатам таблицы 5.4.1, были сделаны следующие основные выводы:

1. Изменение интервала сезонности (Seasonal Lag = 3; 4; 6; 8) при прогнозировании методом авторегрессии и проинтегрированного скользящего среднего показало, что наиболее близкие прогнозируемые значения к фактическим значениям достигаются в большинстве случаев при значении Seasonal Lag=6.

2. Наименьшая ошибка прогнозирования методом авторегрессии и проинтегрированного скользящего среднего составила 0,070643338, а наибольшая – 78,14655803.

3. Наиболее точные результаты, полученные при прогнозировании методом авторегрессии и проинтегрированного скользящего среднего, представлены в таблице 5.4.2.

Таблица 5.4.1