5.6. Предварительная оценка результатов прогнозирования в системе координат

На практике часто возникает необходимость заранее предсказывать ошибку прогноза, которая будет получена при применении того или иного метода прогнозирования. Для этой цели целесообразно использовать эмпирические распределения, которые позволяют получить аппроксимации в тех случаях, когда некоторые моменты распределения определены теоретически, а точное распределение неизвестно. Меррингтон и Пирсон [19] для подбора распределения предложили использовать области в плоскости (), где по осиx откладывается - квадрат нормированного показателя асимметрии, а по осиy откладывается - нормированный показатель островершинности.

Квадрат нормированного показателя вычисляется по формуле

, (5.6.1)

где - дисперсия (второй центральный момент), который можно определить по формуле

, (5.6.2)

- третий центральный момент, который можно определить по формуле

. (5.6.3)

Нормированный показатель островершинности вычисляется по формуле

, (5.6.4)

где - четвертый центральный момент, определяемый по формуле

, (5.6.5)

В формулах (5.6.2) – (5.6.3), (5.6.5) величины ,,- начальные моменты первого, второго, третьего и четвертого порядка соответственно; их можно вычислить по формулам:

,

, (5.6.6)

,

.

Величина измеряет отношение асимметрии распределения к мере рассеяния. Этот нормированный показатель позволяет сравнивать асимметрию двух распределений, имеющих различный масштаб. Величинаявляется относительным показателем эксцесса.

Мною предложено проводить предварительный анализ ВДР, вычисляя значения ии по этим значениям заранее оценивать ошибку прогноза, которая при этом будет получена.

Для обеспечения корректности получаемых результатов предлагается методика, которая включает в себя три этапа:

1. Вычисление величин ипо ВДР;

2. Получение уравнений регрессии, представляющих собой зависимости ошибки прогноза от величин и;

3. Построение графика .

Результаты вычисления иприведены в таблице 5.6.1.

В таблице 5.6.1 z₁ – отношение стандартной ошибки к среднему значению, полученное при прогнозировании методом скользящего среднего; z₂ – отношение стандартной ошибки к среднему значению, полученное при прогнозировании методом экспоненциального сглаживания; z₃ – отношение стандартной ошибки к среднему значению, полученное при прогнозирование методом авторегрессии и проинтегрированного скользящего среднего; z₄ – отношение стандартной ошибки к среднему значению, полученное при прогнозировании на нейронных сетях.

График приведен на рисунке 5.6.1.

Таблица 5.6.1

Вычисленные значения и

j	Основные статистические характеристики ВДР							Отношение ошибки прогноза к среднему значению
				aj	ej			z1	z2	z3	z4
1	202405	145940	0,72103	0,77933	-0,6412	0,525846	2,23471	0,425619863	0,268499171	0,192299	0,093957
2	168375	126916	0,75377	0,83800	-0,5096	0,607998	2,338236	0,582976972	0,259428967	0,375303	0,025906
3	5010	3410	0,680639	1,45767	2,79648	1,839643	4,93926	0,235388066	0,130125992	0,18705	0,062323
4	20808	15359	0,73813	0,88272	-0,0993	0,67462	2,660973	0,496375532	0,308439948	0,131538	0,038304
5	8636	8935	1,034623	2,02198	5,06240	3,539729	6,721968	0,424243204	0,424015193	0,251606	0,052747
6	3398	3385	0,996174	1,39571	1,29295	1,686586	3,756355	0,265790571	0,510646461	0,327121	0,068583
7	1001	1116	1,114885	1,61975	1,91172	2,271501	4,243177	0,529258772	0,321999767	0,683927	0,043091
8	193	290	1,502591	1,52757	0,95457	2,02031	3,490141	0,260025866	0,256100193	0,283076	0,129535
9	28307	27997	0,989049	1,24468	1,07042	1,341323	3,581284	0,472606146	0,979917262	0,539508	0,229634
10	30925	30878	0,99848	1,47047	1,90955	1,8721	4,241468	0,499967477	0,798277021	0,565365	0,120869
11	8326	13769	1,653735	1,41256	0,35724	1,727545	3,020188	68,36838773	19,51832489	38,37432	0,274428
12	11266	15188	1,348127	0,96759	-0,7374	0,810588	2,159006	20,50273748	26,08609931	9,844684	0,176953
13	408	292	0,715686	0,69944	-0,7681	0,423562	2,134824	0,588150888	0,313092341	0,406331	0,024974
14	17	17	1	1,66467	3,45370	2,399239	5,45633	0,424349043	0,415475156	0,554825	0,048905

Далее приведены полученные уравнения регрессии для z₁ – z₄:

(5.6.7)

(5.6.8)

(5.6.9)

(5.6.10)

Ввиду того, что наилучшие результаты прогнозирования были получены при прогнозировании на нейронных сетях, далее приведен график зависимости для уравнения (5.6.10).

Рис. 5.6.1. График

Таким образом, предварительный анализ ВДР позволяет заранее оценить ошибку прогноза по вычисленным значениям и.

Продемонстрируем это на примере результативного показателя y₁₃. По таблице 5.6.1 находим, что значения иравны соответственно0,423562 и 2,134824.

Точка с координатами (0,423562; 2,134824) на рисунке 5.6.1 лежит между прямыми, соответствующими значениям z₄=0,025 и z₄=0,05. Следовательно, можно сделать выводы о том, что ошибка прогноза будет лежать в интервале [0,025; 0,05], что не противоречит результату, полученному после прогнозирования, ошибка прогноза на нейронных сетях для y₁₃ составила 0,024974.

Нужно отметить недостаток предложенного метода. Этим недостатком является наличие зоны неопределенности, для которой невозможно заранее оценить ошибку прогноза, хотя прогнозирование можно проводить и в этом случае. Это объясняется сравнительно небольшим количеством прогнозируемых значений.

Можно надеяться, что с увеличением количества оцениваемых переменных результаты будут охватывать большую область.

* *

*

При проведении временного прогнозирования получены следующие основные результаты:

1. Проведено сглаживание и прогнозирование результативных показателей эффективности функционирования предприятия. Для сглаживания и прогнозирования использованы поквартальные значения результативных показателей эффективности с первого квартала 2000 года по четвертый квартал 2004 года. Проведено прогнозирование на четыре квартала 2005 года. Оценка достоверности произведена по фактическим значениям результативных показателей по трем первым кварталам 2005 года. Применены методы скользящего среднего, экспоненциальный, авторегрессии и проинтегрированного скользящего среднего и на нейронных сетях. Лучшие результаты получены при прогнозировании на нейронных сетях, затем по убыванию качества следует метод авторегрессии и проинтегрированного скользящего среднего, затем экспоненциальный и скользящего среднего. При прогнозировании на нейронной сети отношение стандартной ошибки прогноза к среднему прогнозируемому значению для 14 результативных показателей лежит в диапазоне от 0,025 до 0,274, что следует считать вполне приемлемым для практического использования. Прогнозирование позволяет выявить нежелательные тенденции в изменении состояния предприятия и предотвратить их принятием соответствующих управленческих решений.

2. Разработан алгоритм, позволяющий по основным статистическим характеристикам ВДР вычислить стандартную ошибку прогнозирования для четырех методов. Построен график, который наглядно отображает зависимость стандартной ошибки прогноза в системе координат по оси x и по осиy 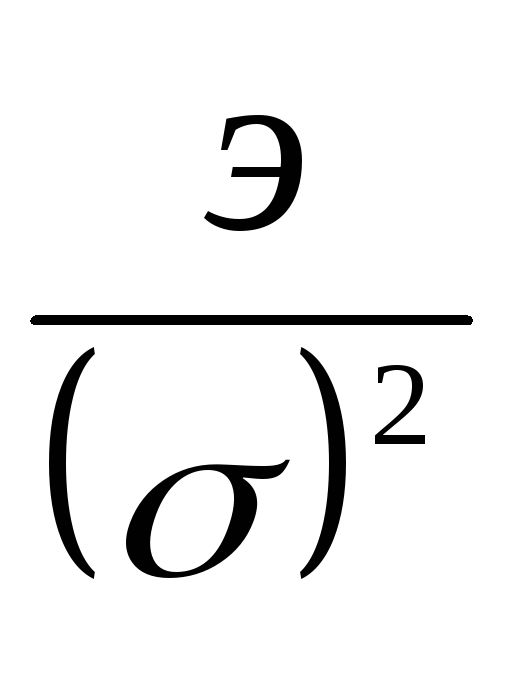, где- оценка дисперсии;а – асимметрия и э – эксцесс, вычисленные по значениям ВДР.