5. Временные динамические ряды.

Сглаживание. Прогнозирование

1. ВДР

2. Сглаживание

3. Прогнозирование

Временные ряды

Временными динамическими рядами (ВДР) называются статистические данные, отображающие развитие изучаемого процесса (явления) во времени.

В качестве фактора в ВДР используются либо даты, либо интервалы времени. В качестве отклика – количественные показатели развития изучаемого процесса во времени.

Основная цель статистического изучения временных динамических рядов (ВДР) состоит в выявлении и оценивании закономерностей их развития.

Основные показатели динамики ВДР

1. Базисный абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем и уровнем, принятым за базу сравнения:

2. Цепной абсолютный прирост (спад) – вычисляется как разность между сравниваемым уровнем и уровнем, который ему предшествует:

3. Базисный темп роста, вычисляется делением сравниваемого уровня на уровень, принятый за базу:

4. Цепной темп роста, вычисляется делением сравниваемого уровня на предыдущий:

5. Базисный темп прироста – вычисляется делением базисного абсолютного прироста на уровень, принятый за базу сравнения:

6. Цепной темп прироста – вычисляется как отношение сравниваемого цепного абсолютного прироста 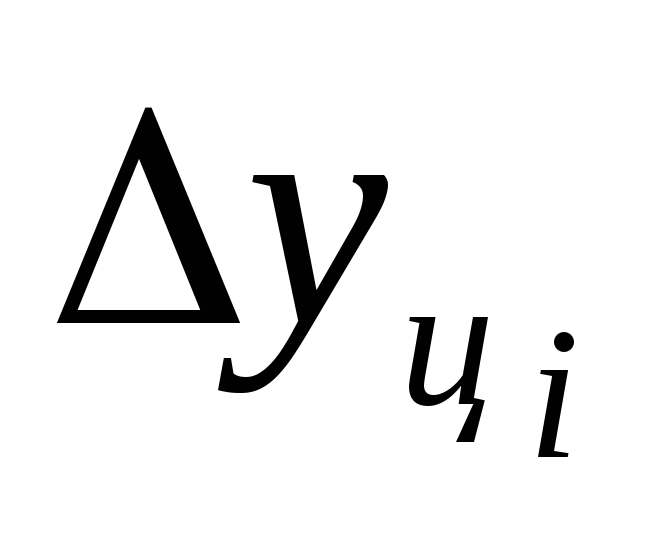к предыдущему уровню:

7. Средний уровень ВДР (оценка математического ожидания):

• для интервального ряда:

• для моментного ряда с равностоящими датами:

• для момента ряда с неравностоящими датами:

7. Средний абсолютный прирост:

7. Средний темп роста:

7. Средний темп прироста:

Проверка гипотезы о существовании тенденции

1. Проверка разности средних уровней:

Разбиваем анализируемый ряд на две примерно одинаковые выборки, каждая из которых рассматривается как некоторая самостоятельная выборочная совокупность. Принимаем допущение, что выделенные выборки подчиняются нормальному закону (можно проверить в ППП Statistica). Воспользуемся методикой, разработанной для малых выборок.

Находим средние значения для левой выборки и правой выборки. Примем допущение об однородности дисперсий. Проверка производится поF-критерию Фишера

(где )

число степеней свободы и;

Принимаем уровень значимости по рекомендации ; если, то гипотезу не отвергаем. В этом случае можно проводить дальнейшую проверку. Выдвигаем гипотезу о равенстве средних и находим критерий Стьюдента:

,

где S – среднее квадратическое отклонение разности средних.

При уровне значимости находим критическое значение критерия Стьюдента дляколичества степеней свободы;

Если , то гипотеза о равенстве средних отвергается. В этом случае можно проводить прогнозирование.

2. Метод Фостера-Стюарта

Вводятся переменные и, которые находятся сравнением по всем уровням. Переменнаяпринимает значение 1, в случае если сравниваемое значение превышает все предыдущие значения ряда, и 0 в остальных случаях.

;

Переменная принимает значение 1, в случае если сравниваемое значение меньше всех предыдущих значений ряда, и 0 в остальных случаях.

;

Вычисляем:

Показатели иимеют независимые нормальные распределения и существенно зависят от порядка расположения уровней во времени.

Показатель используется для обнаружения тенденций в средней

Показатель используется для обнаружения тенденций в дисперсии,

где - математическое ожидание величины, определённое для случайного расположения уровней во времени, берётся по таблице;- средняя квадратическая ошибка величины:

- средняя квадратическая ошибка величины: