
Пвлов_PROCHNOST_2_FULL+PROTECTION
.pdf
, , ,
.
§ 1.2. ( -' -!"$./ ! " #
- - c [2]
,
, . .
. + " . %
, " ,
", , .*, ,
, EJη >> EJξ ~ GJk ,
, - [1]. +
[3].
+ xo . 0
, ,
|
d 2 Y |
0 ( .1.2.1). |
+ , |
|
dz2
d 2 Y0 , . dz2
2[1] .2.7, xz yz:
d 2 X |
d 2 Y0 |
|
d 2 Y |
= |
d 2 Y0 |
cosα , (2.5.1) |
|
|
= |
|
sin α ; |
|
|
||
|
dz |
dz2 |
dz |
||||
dz2 |
|
|
|
||||
ξyζ, ,
ϕ . # 2.+.' [1], ( .1.2.1, ).

!.1.2.1
+ ,2.+.', :
d 2η |
|
= |
|
d 2 X |
ϕ − |
d 2 Y |
; |
||||||||
|
|
|
|
|
|
|
|
|
|||||||
dς |
2 |
|
|
|
|
dz2 |
|
dz 2 |
|
||||||
d 2 ξ |
|
|
d |
|
2 X |
d 2 Y |
|
||||||||
|
|
= |
|
|
|
|
|
+ |
|
|
ϕ ; |
||||
|
|
|
|
|
|
|
|
|
|||||||
dς 2 |
|
|
|
|
dz2 |
dz2 |
|
||||||||
|
|
|
dϕ |
|
|
dϕ |
|
|
|
(1.2.2) |
|||||
|
|
|
|
= |
|
|
|
|
|||||||
|
|
|
|
|
|
. |
|
|
|
|
|||||
|
|
|
dς |
|
dz |
|
|
|
|
||||||
#,5− 5
d 2 ξ |
= |
M η |
d 2 η |
= |
M ξ |
dϕ |
= |
Mς |
, |
|
||
|
|
, |
|
|
, |
dς |
C |
(1.2.3) |
||||
dς 2 |
B |
dς 2 |
A |
|
|
|||||||
A= EJ ξ , = EJ η = GJkp ,−
, ξ ,y,
ζζ:

|
d 2 X |
|
|
|
d 2 Y |
|
|
|||||||||
M ξ |
= A |
|
|
|
|
|
ϕ − |
|
|
|
|
|
|
; |
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dz |
2 |
|
|
|
|
dz |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
d |
2 |
X |
|
|
d |
2 |
Y |
|
|
|||||
M η = B |
|
|
|
+ |
|
ϕ ; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
dz2 |
|
|
dz2 |
|
|
|
|
|||||||
|
(1.2.4) |
||
M ς |
= C |
dϕ |
. |
|
|||
|
|
dz |
|
2 ,
:
|
M ξ = M x |
+ ϕ M y − |
|
dX |
M z ; M η |
= − ϕ M x |
+ M y − dY M z ; |
|
|||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
||
|
|
|
M ς = |
dX |
|
M x + |
dY |
M y + M z . |
(1.2.5) |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
dz |
|
dz |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 Y0 |
|
= |
M xΣ |
|
, |
|
(1.2.6) |
||||
|
|
|
|
|
|
|
|
|
|
|
dz2 |
|
|
AΣ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
M x |
− , ; |
||||||||||||||||||||
A |
− − |
||||||||||||||||||||
, (1.2.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
M x |
= − A |
M xΣ |
cosα , |
|
M y |
= B |
M xΣ |
sinα. |
(1.2.7) |
||||||||||
|
|
AΣ |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AΣ |
|
|||||
+(1.2.4) (1.2.5), (1.2.7) z ,
:
Aϕ X"− AY"= − A |
M xΣ |
|
cosα + ϕ B |
M xΣ |
sinα − X ' M |
|
; |
|
||||||||
|
|
|
|
z |
|
|||||||||||
|
|
AΣ |
|
|
|
|
|
AΣ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
BX"+BϕY"= ϕ A |
M xΣ |
cosα + B |
M xΣ |
sinα − Y' M z ; |
(1.2.8) |
|||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
AΣ |
AΣ |
|
|
|
|||||||
Cϕ '= − X ' A |
M xΣ |
cosα + Y' B |
M xΣ |
|
sinα + M z . |
|
|
|
||||||||
|
AΣ |
|
|
|
||||||||||||
|
|
AΣ |
|
|
|
|
|
|
|
|
|
|
||||

+ (1.2.8) z, ,
M xΣ / AΣ :
Cϕ ′′ = − X" A |
M xΣ |
cosα + Y"B |
M xΣ |
sinα + M z| . |
(1.2.9) |
AΣ |
|
||||
|
|
AΣ |
|
||
X" Y" (1.2.8) (1.2.9):
|
|
|
|
|
|
B − |
A |
M |
xΣ |
|
2 B |
|
|
|
|
B |
|
|
|
|
|
|
|
|
||||||
|
|
|
ϕ"+ |
|
|
|
|
|
|
|
|
sin2 α − |
|
|
cos2 |
α ϕ = |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
C |
|
|
AΣ |
|
|
A |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
B − A |
M xΣ |
|
2 |
|
|
|
|
|
|
|
|
′ |
|
|
M z M xΣ B |
|
|
A |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
M z |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
= |
|
|
sinα cosα + |
|
|
|
+ |
|
|
|
|
|
X 'sinα + Y |
cosα . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
C |
|
AΣ |
|
|
|
|
|
|
|
|
C |
|
|
C AΣ |
|
A |
|
|
B |
|
|
||||||||
(1.2.10)
! ,
xo .
+ |
B |
sin2α > |
A |
cos2α , . . α >α 0 ≈ |
A |
, (1.2.10) |
: |
|||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
A |
|
|||||||||||||||||||||||||||||||||||||
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ϕ 1 = C |
1 cos kz+ C2 sin kz+ |
|
, |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
ϕ |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B − A |
|
|
M |
xΣ |
|
2 |
B |
|
|
|
|
|
|
|
|
A |
|
|
||||||||||
|
|
|
|
|
|
k2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 α − |
|
cos2 |
α ; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
AΣ |
|
A |
|
|
|
|
|
|
|
|
B |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
− A |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
M xΣ |
|
|
|
B |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
ϕ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinα cosα. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
AΣ |
|
|
|
|
|
|
C |
|
|
|
|
|
|
||||||||||
0 z=0, : |
||||||||||||||||||||||||||||||||||||||
1) z=0 6 ϕ =0; 2) z=l 6 ϕ'=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
- C |
|
= − |
|
, C |
|
|
= − |
|
|
sin kl |
, |
|
|
|||||||||||||||||||||||||
|
ϕ |
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
2 |
ϕ |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
coskl |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin kl |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ϕ = − |
ϕ |
coskz+ |
|
|
|
|
|
|
sin kz− 1 . |
(1.2.11) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
coskl |
|
|
|
|
|
|
||||||

* , coskl=0, . . xo
ϕ , M xokp ( .1.2.2, ),
, (1.2.10). 5 M xokp :
M xokp = |
π |
|
AΣ |
|
C |
|
|
A |
|
1 |
|
|
2l sinα |
|
B − |
A B 1 − (A/ B)2 ctg2α . |
(1.2.12) |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!.1.2.2
+ Mx 0
. ! (1.2.10),
.
!
" :
M kp |
≤ M |
" |
= 2 |
σ h |
A . |
(1.2.13) |
xo |
|
|||||
xo |
|
|
hE |
Σ |
||
|
|
|
|
|
|
$ σ h − ;h− .
+(1.2.12) (1.2.13),

l |
|
≥ π |
|
AC |
|
E |
|
1 |
|
|
1 |
|
|
. |
(1.2.14) |
h |
|
B |
|
σ h |
|
sinα |
|
|
|
|
|||||
4 |
|
|
|
|
1− ( A/ B) 2 |
ctg 2 α |
|
||||||||
! (1.2.14) , ,
.
+ α kp h/l σ h, ,
. + ( .1.2.2, )
:
B/A=40, A=C, E=7,2 104 (+, σ 1 h =300(+,
σ 2 h =200(+, σ 3 h =100(+.
! , " ,
".
α kp =α 0. - (1.2.14)
,
l |
= |
π |
|
AC |
|
E |
|
1 |
. |
|
|
|
|
|
|||||
h 4 |
|
B σ h sinα kp |
|||||||
2 α < α0 (1.2.10) .
' ,
, ,
.
+
. * ,
, ,
. 3 , " " – . +
" , ,
.

§1.3. .
1) ,
, ,
[4].
[1] ,
1), 2) « », 3)
« » 4) .
, [14].
!,
[16].
", # , -
. $ %, - , &
& , [2]. ' #
&, ,
«#» .
[3].
( . ( . 1.3.1),
) . *
.
[2],
[3]. + . 1.3.1
. +
2). (, )
, #
1)! , #
.
2), .

, ,
# &. * , ,
. , ,
, .
& ,
.
-
( ). [4] #.
. 1.3.1
! .
* # :
1),
;
2)- ;
3)# &
& ;
4),
[3].

. 1.3.2
! . 1.3.2 , #
# 0
&:
y = y0 cos (α + ϕ),
(1.3.1)
x = y0 sin (α + ϕ).
. α – ;
ϕ – .
! ,
. /
, [16]. $
# # .
,
,
.
*
dz. + 3 # Q
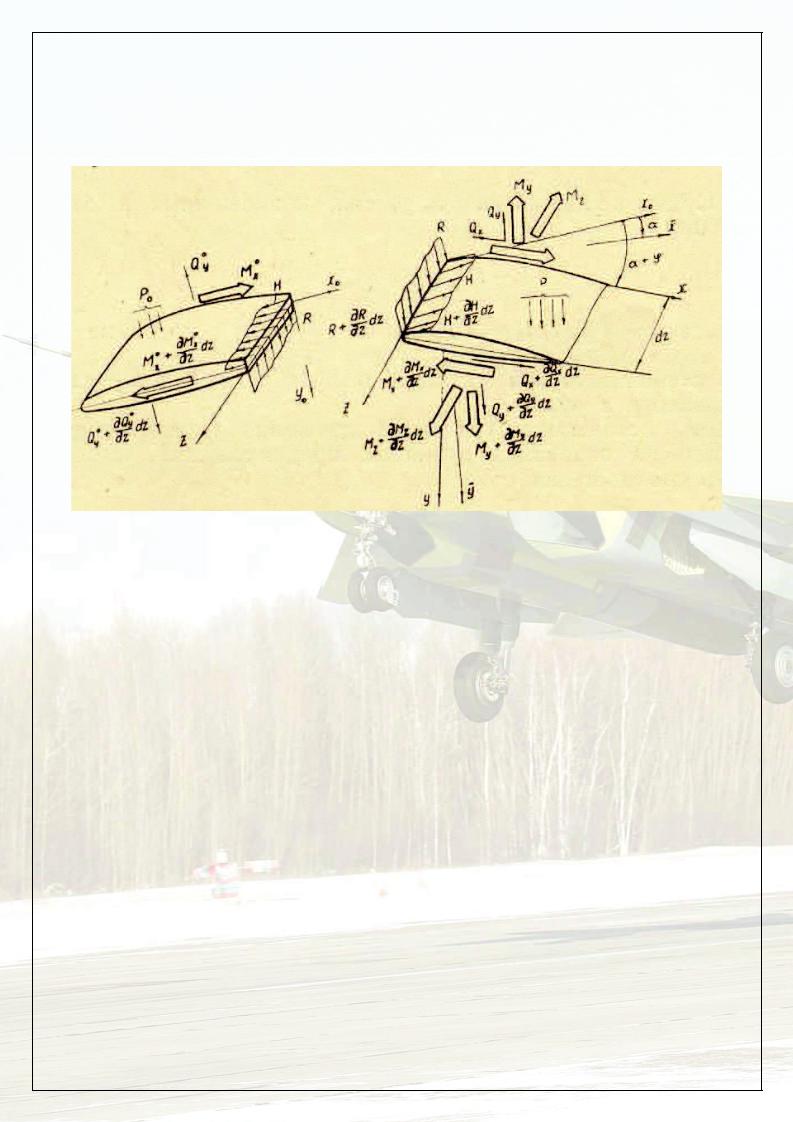
.
& R . 0
0 0 .
. 1.3.3
1 & / , #
, &. * α ϕ , . .
cos (α +ϕ ) =1, |
sin (α +ϕ ) = α +ϕ , |
|
(1.3.1) : |
|
|
y = y0 , |
x = y0 (α +ϕ ). |
(1.3.2) |
. & 0
dP0 = −m |
|
2 0 |
dz, |
|
|
|
|
||
0 τ 2 |
||||
0 |
|
|
|
|
|
2 |
|||
dP = −m |
|
0 |
dz |
|
|
|
|||
|
|
2 |
||
