Oper_Ampl

Глава 4. Логарифмические схемы

Ток IК2 равен выходному току источника постоянного тока на Т3 (IК3). В идеальном случае IК2 устанавливают так, чтобы со- блюдалось численное равенство R1IК2 =1, а сдвиг усилителя 2

kT

ления усилителя 2 выбрать численно равным q , то выходное

напряжение схемы, приведенной на рис. 4.4, будет равно Uвых= =– lnU1. Термистор, включенный в цепь обратной связи опера- ционного усилителя 2, предназначен для компенсации темпера-

kT

турных изменений напряжения q . Без термистора у схемы

будет значительная температурная нестабильность. Эта схема обеспечивает точное преобразование при изменении входного сигнала в диапазоне пяти декад.

130

Глава 4. Логарифмические схемы

-U

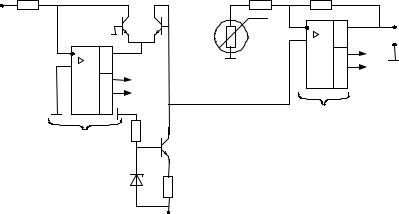
Рис 4.4. Высококачественный логарифмический усилитель (преобразователь)

Транзисторы Т1 и Т2 могут быть заменены подобранными парными диодами. При этом источник постоянного тока дол- жен иметь выходной ток, равный обратному току диода.

4.3. АНТИЛОГАРИФМИЧЕСКИЙ УСИЛИТЕЛЬ

Для нахождения по значениям логарифмов соответствующих им исходных величин (т. е. для получения значений антилога- рифма) требуется найти значение экспоненциальной функции

от логарифма, так как elnX = X .

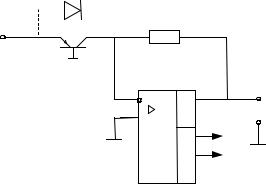
Взяв экспоненту от логарифма, получим антилогарифм. Ис- пользуя схему логарифмирования в качестве входной цепи уси- лителя, как показано на рис. 4.5, получим устройство с экспо- ненциальной характеристикой, т. е. антилогарифмический уси- литель.

131

Глава 4. Логарифмические схемы

Вместо транзистора в качестве входного элемента может ис-

Если входное напряжение должно быть отрицательным, а не положительным, необходимо либо использовать входной тран- зистор n-p-n типа, либо включить диод, если он используется вместо транзистора катодом к U1.

Пример. Построить схему антилогарифмического усилителя, как показано на рис. 4.5. Пусть Ioc=0,1мА при Uвых=10В. Ток IЭО транзистора равен 40нА. Найти величину R.

Решение.

Так как напряжение в точке суммирования примерно равно нулю и IRoc = IK , то

132

Глава 4. Логарифмические схемы

R = 10B = 100кОм . 0,1мА

Пример 4.3. Найти Uвых для схемы из предыдущего примера, если Uвх= 0,1616 и α ≈ 1 (коэффициент эммитерного тока в схе- ме с ОБ).

Решение.

Сравните этот результат с предыдущим примером.

4.4. СХЕМА УМНОЖЕНИЯ

Для построения схемы умножения можно, имея возможность получать значения логарифмов сомножителей, использовать следующее соотношение: ln(A B) = lnA + lnB . Схема умноже- ния строится, как показано на рис. 4.6. Логарифмы величин U1 и U2 суммируются для получения величины, равной lnU1 + lnU2 . Затем для нахождения величины U1 U2 находится антилогарифм от полученной суммы. Схема может иметь боль- ше двух входов, однако для каждого входа требуется свой лога- рифмический усилитель.

Выходное напряжение каждого логарифмического усилителя равно:

Выходное напряжение сумматора равно:

133

Глава 4. Логарифмические схемы

Если Roc IO3 = R1 R2 IO1 IO2 , то Uвых4 = U1U2 .

Величины IО должны быть соизмеримы, и они очень близки к значениям обратного тока IБЭО при малом обратном напряже- нии, приложенном к переходу эмиттер-база. Схема может быть собрана с использованием диодов вместо транзисторов как в логарифмическом, так и в антилогарифмическом усилителях. Предполагается, что все усилители, используемые в схеме, пол- ностью скорректированы.

134

Глава 4. Логарифмические схемы

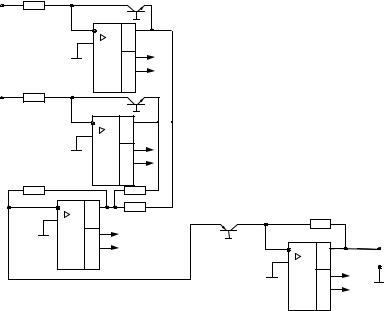
Рис 4.6. Схема умножения аналоговых сигналов

Выпускаются готовые схемы умножения, стабильно рабо- тающие в широком диапазоне изменения внешних условий и температур. Эти схемы являются сложными и тщательно вы- полненными устройствами. Их примерная блок-схема приведе- на на рис.4.6. Некоторые умножители, называемые двухквад- рантными, могут работать только при одной полярности сигна- лов на одном из входов; другие, называемые четырехквадрант- ными, работают при любой полярности сигналов на обоих вхо- дах.

Умножители используются в схемах модуляторов, демодуля- торов, фазовых детекторов, в аналоговых вычислительных уст- ройствах, используемых при управлении технологическими процессами, при генерировании нелинейных колебаний и для линеаризации выходных сигналов преобразователей (датчиков)

135

Глава 4. Логарифмические схемы

в системах сбора данных, причем это лишь некоторые из воз- можных применений умножителей.

4.5. СХЕМА ДЕЛЕНИЯ

Учитывая, что ln A = lnA − lnB , можно использовать тот же

B

принцип, что и в устройстве умножения, для построения схемы деления. Единственным отличием от схемы умножения являет- ся использование дифференциального усилителя вместо инвер- тирующего сумматора. Схема блока деления приведена на рис. 4.7.

Сигналы на выходах логарифмических усилителей будут равны:

Для получения U1 выходное напряжение логарифмического

U2

усилителя 1 подается на неинвертирующий вход, а выход лога- рифмического усилителя 2 – на инвертирующий вход диффе- ренциального усилителя. Напряжение на выходе последнего будет равно:

Приняв, как обычно, IО1≈ IО2 и R1=R2, получим:

136

Глава 4. Логарифмические схемы

U1

ln U1

∞

+U - U

ln U2

∞

+U

Ln U2 − Ln U1 = Ln U1 - U

U2

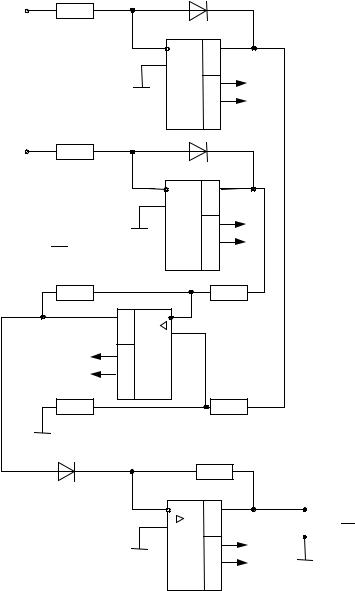
Рис 4.7. Схема деления аналоговых сигналов

137

Глава 4. Логарифмические схемы

На выходе антилогарифмического преобразователя напряже- ние будет равно:

Если величина IО3 такова, что произведение RocIО3 может

Высококачественные устройства деления точно так же, как и устройства умножения, имеются в продаже. Область примене- ния этих схем фактически та же, что и для устройств перемно- жения.

4.6. СХЕМА ПОЛУЧЕНИЯ ЛОГАРИФМА ОТНОШЕНИЯ

Напряжение на выходе дифференциального усилителя в схе- ме, приведенной на рис. 4.7, является логарифмом отношения входных величин и равно

где Roc – сопротивление обратной связи; R1 – входные сопро- тивления дифференциального усилителя. Схема, состоящая из двух логарифмических усилителей и дифференциального уси- лителя, соединенных, как показано на рис. 4.7, известна под на- званием “схема получения логарифма отношений”.

4.7. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ

Любая нелинейная зависимость может быть аппроксимиро- вана последовательностью прямолинейных отрезков, имеющих различный наклон. Благодаря этому можно реализовать широ- кий класс нелинейных функциональных преобразователей с

138

Глава 4. Логарифмические схемы

помощью операционных усилителей. Пример схемы преобразо- вателя, иллюстрирующий только что изложенный принцип, приведен на рис. 4.8 а.

Наклон графика зависимости выходного напряжения от

ловии, что входное напряжение меньше напряжения отпирания стабилитрона Д1 на рис. 4.8.б. При значениях входного напря- жения U1, заключенных между Uст1 и Uст2 , выходное напряже- ние будет равно:

U = − U1Roc − (U1 −Uст1 )Roc .

При этом наклон графика зависимости выходного напряже- ния от входного станет равным:

139