
Лекции
.pdf
q1 = z1/2p . m1 = 12/2.1.3 = 2 паза на полюс.
Соединение фаз – звезда.
Теперь нарисуем развертку цилиндрической внутренней поверхности статора с указанием пазов статора (рис. 2.4).
1 |
2 |
3 S 4 |
5 |
6 |
7 |
8 |
9 N 10 11 12 |
1 |
|
I |
|
|
I |
|
I |
|
I |
|
|
|
|
|
|
|
С6 |
С4 |
С5 |
С1 |
С2 |
С3 |
Рис. 2.4. Схема трехфазной однослойной двухполюсной статорной обмотки
Вначале построим катушечную группу, образующую один полюс одной фазы, для этого нужно занять два паза. При однослойной обмотке одна сторона катушки займет один паз, вторая – второй и катушечная группа будет состоять из одной катушки. Стороны катушки должны отстоять друг от друга на шаг у1, т.е. на 5 пазовых делений, т.е. если положить одну сторону катушки в паз 1, то вторую сторону этой катушки нужно положить в паз 6.
Если пропустить по катушке постоянный ток I, то по правилу правого буравчика можно определить направление магнитного потока. В данном случае, магнитный поток левой катушки входит в плоскость развертки. Таким образом, эта катушка образует южный полюс S. Для того чтобы образовать северный полюс N, нужно уложить еще одну катушку и соединить ее так, чтобы она образовала полюс N. Для этого одна сторона второй (правой) катушки укладывается в паз 7, а вторая – в паз 12 и соединяется, как показано на рис. 2.4. Теперь делаем маркировку фазы: С1 – начало фазы, С4 – конец фазы.
Схема второй фазы такая же, только начало фазы должно быть сдвинуто относительно первой на 120 электрических градусов:
αэл = р . αгеом → αгеом = αэл/р = 120о/1 = 120о.
Таким образом, для построения второй фазы надо сместить начало второй фазы на 4 пазовых деления и поместить сторону первой (левой) катушки второй фазы в паз 5, а вторую сторону катушки – в паз 10. Вторую (правую) катушку второй фазы укладываем в пазы 11 и 4 соответственно. Вторую фазу будем обозначать пунктиром.
41

Третью фазу обозначим штрихпунктиром и сместим относительно второй фазы также на 120о, т.е. поместим начало третьей катушки в паз 9, а далее – по аналогии. Критерием правильности построения схемы является занятость всех пазов или, другими словами, расположение в каждом пазу одной стороны катушки.
Схема двухслойной трехфазной двухполюсной статорной обмотки. Исходные данные для построения:
–число фаз статора m1 = 3;
–число пазов статора z1 = 12;
–число пар полюсов p = 1.
Далее определим величину полюсного деления: τ1 = z1/2р = 12/2.1 = 6 пазовых делений. Выберем диаметральный шаг катушки:
y1 = τ1= 6 пазовых делений.
q1 = z1/2p . m1 = 12/2.1.3 = 2 паза на полюс.
Соединение – звезда.
Теперь нарисуем развертку цилиндрической внутренней поверхности статора с указанием пазов статора (рис.2.5).
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
C1 |
C4 |
Рис.2.5. Схема фазы трехфазной двухслойной двухполюсной статорной обмотки
Полюсная группа будет состоять из двух катушек, смещенных в пространстве на одно пазовое деление, потому что каждая сторона катушки должна занимать половину паза, т.к. обмотка двухслойная.
Две другие фазы будут точно такими же, но сдвинуты относительно первой на 120 и на 240 электрических градусов. Правильность построения схемы статорной обмотки характеризуется заполнением всех пазов и в каждом пазу должны быть две стороны двух разных катушек.
Отметим, что статорные обмотки синхронных машин выполняются таким же образом.
Если на двигателе имеется маркировка 380/220, то статорную обмотку можно включать звездой или треугольником в зависимости от линейного напряжения сети. Если линейное напряжение Uл= 380 В, то Uф = Uл/1,732=220 В и обмотку двигателя необходимо соединить звездой. Если Uл= 220 В, то Uл= Uф =220 В и обмотку двигателя необходимо соединить треугольником. В обоих
42

случаях фаза статорной обмотки будет работать при номинальном фазовом напряжении 220 В.
2.4. ОБМОТОЧНЫЙ КОЭФФИЦИЕНТ СТАТОРНОЙ ОБМОТКИ
Магнитодвижущая сила (МДС) всех обмоток переменного тока, расположенных на статоре или роторе электрической машины, должна создавать в ее воздушном зазоре вращающееся магнитное поле. Для этого каждая из обмоток, питающаяся от синусоидально изменяющегося напряжения, должна иметь МДС, синусоидально распределенную в пространстве, т.е. по расточке статора. Несоблюдение этих условий, т.е. питание от несинусоидального напряжения или несинусоидальное распределение МДС, приводит к появлению высших гармоник в кривой распределения магнитного потока, что ведет к ухудшению энергетических показателей машины. Получение абсолютно синусоидального распределения МДС, вследствие дискретности обмоток, практически невозможно, однако для приближения к этой цели применяют различные меры конструктивного характера.
Коэффициент укорочения статорной обмотки.
Коэффициент укорочения статорной обмотки учитывает уменьшение ЭДС в катушке или секции за счет укорочения шага.
Пусть статор создает синусоидально распределенную по окружности волну магнитной индукции В, перемещающуюся с линейной скоростью v, и
B |
пусть у1<τ1 (рис. 2.6). |
|
ка- |
||
|
Вначале |
рассмотрим |
|||
v |
тушку с диаметральным шагом |
||||
|
у1=τ1. Обе стороны катушки нахо- |
||||
|
дятся под амплитудным значени- |
||||
α |
ем магнитной индукции В. При |
||||
(1/5)τ1 |
перемещении |
волны |
магнитной |
||
y1 |
индукции в |
них индуктируется |
|||
|
|||||
y1=τ1 |
наибольшее |
значение |
ЭДС. |
В |
|
витке ЭДС складываются. Сум- |
|||||
|
|||||
Рис. 2.6. Волна магнитной индукции |
марная ЭДС будет равна |
|
|||
ΣЕ = Е1 + Е2, |
|
(2.4) |
|||
в развертке статора |
|
||||
а по величине ΣЕ = 2Е, если Е1 = Е2 = Е.
Если шаг укороченный, то максимальные значения ЭДС в сторонах катушки будут достигаться не одновременно и они будут сдвинуты по фазе относительно друг друга (рис. 2.7). Уменьшение суммарной ЭДС в этом случае можно учесть коэффициентом укорочения
ΣE
(y1/τ1) π/2  E2
E2
E1
Рис. 2.7. Векторная диаграмма ЭДС в катушках с укороченным шагом
43
|
|
|
|
|
|
|
y1 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ΣE |
|
2 E sin |
τ1 |
2 |
|
|
y1 |
|
π |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
K y |
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
(2.5) |
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
E |
2 |
E |
|
|
|
= sin |
τ1 |
2 |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Это коэффициент укорочения для первой гармоники магнитной индукции. Для ν-той пространственной гармоники магнитной индукции в периоде первой гармоники будет содержаться ν-периодов высшей гармоники. Поэтому угол между сторонами катушки будет увеличиваться в ν раз. Отсюда коэффициент укорочения для ν-той пространственной гармоники магнитной индукции
|
|
|
|
ν y1 |
|
π |
|
|
|
K yν |
= |
sin |
|
|
|
(2.6) |
|||
|
|
||||||||
|
τ1 |
2 |
. |
||||||
|
|
|
|
|
|
|
Цель укорочения шага катушки состоит не только в уменьшении расхода обмоточного провода, но и в улучшении спектрального состава ЭДС статорной обмотки.
Можно сделать укорочение шага такое, что ЭДС от первой гармоники магнитной индукции уменьшится незначительно, а ЭДС от высшей гармоники – значительно или даже будет равной нулю.
Пример. Укоротим шаг катушки на 1/5 τ1 , тогда у1 = (4/5) τ1. Определим коэффициент укорочения для первой и пятой гармоник:
|
|
y1 |
|
π |
|
|
|
|
4 |
|
τ1 |
|
π |
|
|
2 |
|
|
o |
|
K y1 |
|
|
|
|
|
|
|
|
|
= sin |
π = sin 72 |
≈ 0,9 |
||||||||
= sin |
τ1 |
2 |
|
= sin |
5 |
τ1 |
2 |
|
5 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5 |
4 |
τ1 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
K y5 |
5 |
|
= sin 2π = 0 |
|
|
|
|
|
|
|||||||||||
= sin |
|
τ1 |
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
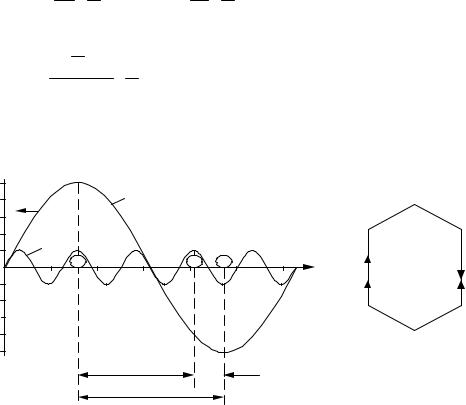
Физически это означает, что ЭДС в сторонах катушки от первой гармони- |
||||||||||||||||||||
ки в витке действуют согласно, а от пятой гармоники – встречно (рис. 2.8). |
||||||||||||||||||||
1 |
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,8 |
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
B5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
1 |
|
|
2 |
|
|
3 |
|
4 |
|
|
5 |
6 |
|
α |
|
|
||||
-0,2 |
|
|
|
|
|
|
|
|
E5 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E5 |
||
-0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
y1=(4τ1)/5 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
τ1/5 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
τ1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.8. Пространственные гармоники магнитной индукции и направления ЭДС от первой и |
||||||||||||||||||||
|
пятой гармоник в катушках с диаметральным и укороченным шагом |
|||||||||||||||||||
44

Коэффициент распределения статорной обмотки.
Пусть полюсная группа образована тремя катушками с диаметральным шагом, сдвинутыми относительно друг друга на электрический угол α. Волна магнитной индукции на рис. 2.9 не указана.
1 |
2 |
Катушки 1, 2, 3 в катушечной группе |
|||
соединены последовательно и ЭДС этих |
|||||
|
3 |
катушек суммируются с учетом сдвига |
|||
α α |
α α |
фаз; ЭДС первой катушки Е1, второй – Е2, |
|||
третьей – Е3. Если бы катушки не были |
|||||
|
τ1 |
сдвинуты по фазе, то суммарная ЭДС ΣЕ = |
|||
|
3Е, где Е – ЭДС каждой фазы. |
|
|||
Рис. 2.9. Развертка статора с полюс- |
В случае сдвига катушек на электри- |
||||
ческий угол: |
|
|
|||
ной группой из трех катушек с диа- |
|
π b |
|
|
|
метральным шагом |
α= |
, |
(2.7) |
||
|
|
τ1 |
|||
|
|
|
|
|
|
где b – расстояние между осями соседних пазов, векторная диаграмма имеет
вид, показанный на рис. 2.10: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Коэффициент |
|
|
распределения |
статорной |
|
|
|
|
|
|
E3 |
|
||||||||||||
обмотки можно записать в виде: |
|
|
|
|
|
|
|
|
|
|
ΣE |
|||||||||||||
|
|
|
|
|
|
|
|
|
α |
|
||||||||||||||
|
|
Σ E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
K р1 = |
. |
|
|
|
|
|
(2.8) |
|
|
|
|
|
|
|
E2 |
|
|
|||||||
3 E |
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
||||||
Из треугольника ОАС следует, что |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
E |
|
|
|
|
|
|
q .α |
||||||||||||||
АС = ОA.sin(q1α/2). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
В |
1 |
|
|
|
α |
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Из треугольника ОАВ можно записать вы- |
|
|
|
|
|
|
O |
|||||||||||||||||
ражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
||||
АВ = ОA.sin(α/2) = E/2, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
тогда коэффициент распределения для первой гар- |
|
|
Рис.2.10. Векторная диаграмма |
|||||||||||||||||||||
|
|
|
|
|
ЭДС полюсной группы |
|||||||||||||||||||
моники магнитной индукции будет: |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
K р1 = ΣE |
|
|
|
|
2 AC |
|
|
OA sin |
q1 α |
|
sin |
q1 α |
|
|
|
|||||||||
|
= |
|
= |
|
2 |
= |
|
2 |
|
|
, |
|
(2.9) |
|||||||||||
|
3 2 AB |
|
|
|
|
|
|
|||||||||||||||||
3E |
|
|
|
|
3 OA sin |
α |
|
q1 sin |
α |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поскольку для рассматриваемого случая q1=3. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Для ν-той гармоники он имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
sin |
|
ν |
q1 α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
K рν = |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
q1 sin |
|
ν α . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.10) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
45

Рассмотрим пример. Выясним, на какой угол нужно сдвинуть катушки, чтобы коэффициент распределения от пятой гармоники был равен нулю (Кр5=0), т.е.
sin |
ν q1 α |
|
=0 → |
ν q1 α |
|
=π → |
ν=5, |
q1 =3 →α=24o . |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
Коэффициент распределения для первой гармоники при таком сдвиге бу- |
||||||||||||||||||||||
дет: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
sin |
q1 α |
|
|
|
|
sin |
|
3 24 o |
|
|
|
|
sin 36 o |
|
||||||
K р1 = |
2 |
|
|
= |
|
2 |
|
|
= |
|
≈ 0,94 . |
|||||||||||
|
|
α |
|
|
|
|
|
o |
|
|
o |
|||||||||||
|
|
q1 |
sin |
|
|
|
|
3 sin |
24 |
|
|
|
|
3 |
sin 12 |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
Распределение катушек способствует уменьшению ЭДС от высшей пространственной гармоники магнитной индукции. Высшие пространственные гармоники магнитной индукции в воздушном зазоре обусловлены дискретным распределением статорной обмотки в пазах.
Коэффициент скоса статорной обмотки.
Скос пазов выполняется на роторе или на статоре на одно пазовое (зубцовое) деление. Пусть скос пазов выполнен на статоре на угол скоса γск радиан (рис. 2.11). Разделим высоту развертки статора на некоторое количество равных частей, теперь скошенную часть паза можно в пределах одной части заменить верти-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кальной частью паза. |
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В каждой вертикальной части нахо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дятся проводники условных катушек, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
γск |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сдвинутые относительно друг друга на |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угол α. Значит, скос эквивалентен распре- |
|||||||
Рис. 2.11. Скос пазов статорной обмотки |
делению катушек и коэффициент скоса по |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аналогии с коэффициентом распределения |
можно записать по формуле (2.9) в виде: |
||||||||||||||||||||||||
|
|
|
sin |
q1 α |
|
|
|
sin |
|
γск |
|
|
||||||||||||
K ск 1 = |
|
|
2 |
|
|
|
= |
|
|
|
2 |
, |
(2.11) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
q1 sin |
α |
|
|
|
γск |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поскольку угол α мал, и можем использовать формулу: |
||||||||||||||||||||||||
q1 sin |
|
α |
|
≈ |
|
q1 α |
|
= |
γск |
. |
|
|
|
|
(2.12) |
|||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||
Для ν-той гармоники коэффициент скоса равен:
|
sin |
ν |
|
γ ск |
|
|
|
||
K ск ν = |
|
|
|
2 |
|
|
. |
(2.13) |
|
|
|
|
|
|
|
||||
ν |
|
γ |
ск |
|
|
||||
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
46

Таким образом, скосом пазов также можно влиять на уменьшение ЭДС от высших гармоник магнитной индукции.
Обмоточный коэффициент статорной обмотки. Обмоточный коэффициент статорной обмотки равен:
Коб1 = Ку1.Кр1.Кск1. |
(2.14) |
Поскольку каждый из коэффициентов меньше единицы, то и обмоточный коэффициент Коб1<1. Чаще всего он находится в диапазоне Коб1 = 0,707÷0,96, причем для двухфазной статорной обмотки характерна наименьшая величина Коб1. Обмоточный коэффициент для высших гармоник
Кобν = Куν. Крν. Кскν << 1.
2.5. МДС СТАТОРНОЙ ОБМОТКИ
МДС фазы статорной обмотки.
Пусть фаза статорной обмотки образована одной катушкой с диаметральным шагом. Статор и ротор разделены воздушным зазором δ’ в десятые доли мм. Пусть в катушке протекает амплитудное значение переменного тока Im с указанным направлением (рис. 2.12), число витков катушки Wк равно числу витков фазы Wф.
Hδ'.δ'
Lр
Lс
α
A |
Х |
начало фазы |
конец фазы |
δ'
Рис. 2.12. МДС катушки с диаметральным шагом
Вокруг проводника с током возникает магнитный поток, который можно показать линиями магнитной индукции или напряженности. Направление линий определяется по правилу правого буравчика. Для каждой линии можно записать закон полного тока:
Im Wф = Hc1 Lc1 + Hp Lp + Hδ' 2 δ' , |
(2.15) |
47

где Lс1 – длина магнитной линии в статоре, Lр – в роторе. Напряженность магнитного поля в статоре равна нулю,
нитную проницаемость стали статора можно считать равной µс1
H c1 = |
Bc1 |
= 0. |
|
||
|
µ c1 |
|
поскольку маг- =∞.
(2.16)
Аналогично и для ротора: |
|
|
|
|||
Hp = |
Bp |
= 0. |
|
|
(2.17) |
|
|
|
|
||||
|
µp |
|
|
|
||
Тогда закон полного тока можно записать в виде |
|
|||||
Im Wф = 2 H δ' δ' → H δ' δ' = |
Im Wф |
. |
(2.18) |
|||
2 |
||||||
|
|
|
|
|
||
Это МДС фазы, приходящейся на один полюс. Для обмотки статора с р парами полюсов данная формула приобретает вид:
f = H δ' δ' = |
I m W ф |
. |
(2.19) |
|
|||
|
2 p |
|
|
Из формулы следует, что МДС воздушного зазора на полюсном делении распределена равномерно. Выделим из прямоугольного распределения МДС ее первую гармонику. Тогда мгновенное значение первой гармоники МДС фазы А можно записать в виде
fA = Fm cosα sin(ω t), |
(2.20) |
где Fm – амплитудное значение первой гармоники МДС фазы; cos α учитывает косинусоидальное распределение МДС по окружности статора; sin ωt – синусоидальное изменение тока в фазе.
Учитывая (2.19) и то, что амплитуда Fm первой гармоники в 4/π раз больше высоты прямоугольного распределения МДС, получим амплитудное значение первой гармоники МДС в общем виде:
Fm = |
4 |
|
Im Wф |
Kоб1 |
= |
2 |
|
2 |
I Wф Kоб1 |
= 0,9 |
I Wф Kоб1 |
, |
(2.21) |
|
π |
2 |
p |
|
π |
|
p |
p |
|||||||
|
|
|
|
|
|
|
|
|
||||||
где Коб1 учитывает укорочение шага катушки, распределение катушки, скос пазов.
МДС двухфазной обмотки.
В двухфазном асинхронном двигателе обмотки пространственно сдвинуты относительно друг друга на 90 электрических градусов (рис. 2.13). Токи в фазах также сдвинуты относительно друг друга на 90о электрических градусов.
МДС фазы А
fA = Fm sin(ω t) cos α. |
(2.22) |
48

МДС фазы В можно записать в виде |
|
|
|
|
|
|
|
|
|
|||
fB = Fm sin (ω t − 90o ) cos(α − 90o ). |
|
|
|
|
|
|
(2.23) |
|||||
Тогда МДС двух фаз будет равна: |
|
|
|
|
|
|
|
|
|
|||
f2ф |
= f A + f B = |
(sin ωt cos 90 |
|
|
|
|
) |
|
|
|
||
= F |
|
o |
|
− cos ωt sin 90 |
o |
|
= |
|
||||
sin ωt cos α + |
|
|
|
|
(2.24) |
|||||||
|
m |
o |
+ sin α |
sin 90 |
o |
) |
|
|
|
|
||
|
(cos α cos 90 |
|
|
|
|
|
|
|
||||
= Fm (sin ωt cos α − cos ωt sin α)= Fm sin (ωt − α). |
|
|
|
|
|
|||||||
Это выражение говорит о том, что ампли- |
|
|
|
|
|
|||||||
тудное значение МДС двухфазной обмотки равно |
|
|
|
|
|
|||||||
амплитуде МДС одной фазы. МДС распределена в |
|
|
|
|
B |
|||||||
пространстве синусоидально и вращается с угло- |
|
|
|
|
|
|||||||
вой скоростью ω. |
|
|
|
|
|
A |
|
|
|
|
X |
|
То, что МДС вращается, можно пояснить |
|
|
|
|
|
|||||||
следующим образом. Проследим место нахожде- |
|
|
|
|
|
|||||||
ния амплитуды МДС двухфазной обмотки в раз- |
|
|
|
|
|
|||||||
личные моменты времени. Для этого потребуем, |
|
|
|
|
Y |
|||||||
чтобы значение ωt−α=π/2, тогда |
sin(π/2)=1 и |
|
|
|
|
|
||||||
f2ф=Fm.
С увеличением времени t должен увеличиваться и пространственный угол α, чтобы выполнялись принятые нами условия. Видно, что угол α изменяется пропорционально электрическому углу
ωt. Тогда можно сказать, что за период изменения тока амплитуда МДС переместится на 2π радиан.
МДС, у которой скорость перемещения и амплитуда не изменяются, называется круговой. Значит, величину ω (временную угловую частоту), можно рассматривать как геометрическую угловую скорость ω1 перемещения двухфаз-
ной МДС. |
|
|
|
|
ω t =2π f t , f = |
1 |
→ ω T =2π → ω1 =2π f . |
(2.25) |
|
T |
||||
|
|
|
За период изменения тока МДС проходит путь, равный длине окружности, на которой располагаются статорные обмотки, образующие одну пару полюсов. Если статорная обмотка будет иметь р-пар полюсов, то статорные обмотке, образующие одну пару полюсов, будут занимать 1/р длины окружности. Тогда за период изменения тока МДС повернется на 1/р часть окружности и угловая скорость МДС будет в р раз меньше. Следовательно выражение для угловой скорости приобретет вид:
ω1 = |
2 π f |
, |
рад |
, |
(2.26) |
|
p |
с |
|||||
|
|
|
|
49
и МДС двухфазной обмотки будет:
|
|
|
ω t |
|
|
|
F2 ф |
= |
|
|
(2.27) |
||
|
||||||
Fm sin |
p |
− α . |
||||
|
|
|
|
|
Частота вращения МДС |
|
|||||
n1 = |
60 |
f |
, |
об |
. |
(2.28) |
p |
|
|
||||
|
|
|
мин |
|
||
МДС трехфазной обмотки статора.
В этом случае фазы в пространстве и токи в фазах сдвинуты на 120 электрических градусов. Поэтому можно записать МДС фаз:
f A = Fm |
sin ωt cos α ; |
|
||
f |
B |
= F |
sin (ωt −120 o ) cos (α −120 o ); |
(2.29) |
|
m |
sin (ωt − 240 o ) cos (α − 240 o ). |
||
f |
C |
= F |
|
|
|
m |
|
|
|
МДС трехфазной обмотки |
|
|||
f3ф = fA + fB + fC . |
(2.30) |
|||
Далее проделываем те же самые операции, как для МДС двухфазной обмотки и получаем:
f3ф |
= |
|
3 |
Fm sin (ωt − α), для р = 1; |
(2.31) |
||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
f |
|
= 3 |
F |
|
ωt |
|
|
|
|||
3ф |
sin |
− α |
, для р > 1. |
(2.32) |
|||||||
|
|
2 |
m |
|
p |
|
|||||
|
|
|
|
|
|
|
|
||||
Некоторые выводы.
1.Пульсирующие во времени и сдвинутые в пространстве МДС образуют вращающуюся МДС
2.Чтобы МДС была круговой, нужно выполнить три условия:
1)МДС фаз должны быть одинаковыми;
2)в пространстве МДС должны быть сдвинуты: для трехфазной обмотки на 120, а для двухфазной обмотки на 90 электрических градусов;
3)токи в фазах должны быть сдвинуты соответственно на 120 и 90 электрических градусов.
3.Если хотя бы одно из этих условий не выполняется, то вращающаяся МДС будет эллиптической с изменяющейся амплитудой и изменяющейся угловой скоростью.
Если МДС изобразить в виде вектора, то конец вектора в случае круговой МДС будет описывать окружность, а в случае эллиптической – эллипс.
Эллиптическую МДС в трехфазных АД иметь нежелательно, так как ее условно можно разложить на две круговые МДС – прямую и обратную. Обратновращающаяся МДС создает (тормозящие) паразитные моменты в электродвигателе.
50
