Лекции по антеннам

151

Различные ДН формируются за счет различного АФР, которое зависит от формы зеркала.

Линзовые антенны:

> 1 Электромагнитная волна (со сферическим или цилиндрическим фронтом) преобразуется в линзе: в

диэлектрическое тело, металлопластинчатой конструкция и т.д.) и в плоскую, за счет преломления лучей.

Применяются линзы (по способу реализации):

1)диэлектрические;

2)металлопластинчатые;

3)металловоздушные (геодезические); 4)металлодиэлектрические;

5)диэлектрические дырчатые;

Различные ДН формируются за счет формы линзы.

Задачу по анализу системы можно разбить на две: внешнюю и внутреннюю.

Внешняя задача заключается в расчете поля,по известному АФР поля в раскрыве и формы раскрыва, определение АФР поля в раскрыве, которое находится методом геометрической оптики, используя в предоставление о лучах: при рассмотрении отражения волны от зеркала и распространении еѐ от зеркала до раскрыва в зеркальной антенне.

Антенны и законы преломления лучей в линзовых антеннах.

Классификация зеркальных и линзовых антенн.

Параболические ЗА создают остронаправленное излучение

(узкую ДН)

Сферические ЗА позволяют качать луч в широких пределах без искажения его формы, перемещая облучатель по дуге окружности R/2.

152

Плоское зеркало используется в качестве рефлектора вибраторных антеннах,

в уголковых антеннах и в перископических антеннах для изменения

специальной формы, например «косекансной ДН».

По числу используемых зеркал различают однозеркальные и многозеркальные чаще двухзеркальные.

Для уменьшения веса и ветровых нагрузок зеркало часто делается перфорированным (d<0,2λ-диаметр отверстия) или сетчатым (h<0,1λразмер ячейки)

Суммарная площадь отверстий не должна превышать 0,5…0,6 всей площади зеркала.

Для характеристики эффективности не сплошных зеркал используют коэффициент прохождения Т=Рпр/Рпад, где Рпр – мощность, просочившаяся за зеркало, Рпад – мощность падающей волны.

Если Т<0,01 – зеркало считается хорошим.

Для тонких зеркал KHД антенн уменьшается за счет уменьшения заднего излучения.

По форме профиля ЛА различают: если лучи преломляются на одной поверхности, то линза называется однопреломляющей, если на обеих поверхностях, то – двухпреломляющей.

Чаще применяют одноприломляющие линзы с плоской теневой поверхностью.

Преломление будет если Vср≠С причем если: Vср<C, n>1 – замедляющие линзы. Если Vср>С, n<1 – ускоряющие линзы.

Когда величина n постоянна линза называется однородной, если меняется т.е. n=f(M), M Vлинзы, то линза называется неоднородной.

Простейшие замедляющие линзы – это линзы из однородного диэлектрика.

153

Если преломление лучей происходит на освещенной поверхности, то линза д.б. выпуклой. При этом центральный участок фронта волны замедляется больше за счет распространения в диэлектрике, чем крайние его участки, то есть происходит выпрямления фронта волны и преобразования его в плоский. Отметим, что плоский фронт формируется уже в теле линзы.

Достоинства однородных линз: не критичность к поляризации и диапозонность (т.к. n слабо зависит от частоты).

Недостатки: большой вес, трудность изготовления линзы, значительные потери в диэлектрике.

Ускоряющие линзы Н – плоскостная линза относится к линзам с вынужденным распространением луча.

Цилиндрические ЗА и ЛА формируют остронаправленное излучение только в одной плоскости.

Осесимметричные антенны в двух плоскостях.

Основные геометрические соотношения.

Поле в раскрыве ЗА и ЛА должно быть синфазно, поэтому лучи должны проходить от источника равные электрические пути.

Параболоид вращения для формирования остронаправленного излучения.

Поверхность параболоида образуется за вращения параболы:

x2 = 4fz = 2pz (13.1)

вокруг фокальной оси (ось Z).Здесь f - фокусное расстояние, p = 2f –

параметр параболы.

154

Полученная поверхность определится в декартовой системе координат уравнением:

Точка 0 – вершина параболоида (зеркала). Положение точки в раскрыве параболоида вращения определяется полярными координатами

если же Z0>f (2 0 > ) – глубоким или короткофокусным.

Ускоряющая линза.

Поверхность линзы является в зависимости от типа излучателя частью эллипсоида вращения или эллиптического цилиндра.

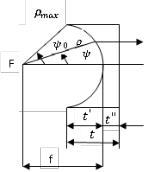
Толщина линзы:

156

t’=(0,33…0,7)d – для ускоряющих линз.

АР веѐраскрыве.

Влияние линзы приводит к спаданию поле к краям раскрыва т.к.

одинаковым углам соответствуют участки х , увеличивающиеся к краям раскрыва х2 > х1

Для ускоряющей линзы амплитуда поля будет к краям раскрыва растет, т.к. Х 2 < Х1

157

Амплитудное распределение в раскрыве

Распределение фазы поля в раскрыве считаем постоянным.

Для простоты рассмотрим цилиндрическую линзу с линейным облучателем и прямоугольным раскрывом АР в плоскости образующей цилиндра А2(y)

совпадает с АР в линейном облучателе АР в плоскости профиля линза А1(х)

находится из закона сохранения энергии в геометрической трактовке его потерями в линзе и потерями на отражения пренебрегаем.

Прировняем друг к другу потоки мощности в пределах угла и отрезках

Х :

Где P0 ( ) - угловая плотность потока мощности, излучаемая единицей длины линейного облучателя, П(Х) - плотность потока мощности в раскрыве линзы.

Переходя к дифференциалам, из (13.16) имеем:

Учитывая, что X sin и используя уравнение для замедляющей линзы,

получим

(n 1) sin X f n cos 1

F0 2 ( ) P0 ( ) ,

P0

Подставляя (13.18) в (13.17) и вводе нормированнуюДН облучателя по мощности получим следующее выражение для амплитуды поля в раскрыве

Методика расчета ДН ЗА и ЛА.

По известному АФР необходимо найти поле излучения, т.е. ДН.

Ограничимся рассмотрением поля излучения и ДН в главных плоскостях.

Как обычно поле антенны в дальней зоне будет

Далее если ДН облучателя осесимметричная АР не зависит от , тогда

множитель системы определяется соотношением

Найденное АР аппроксимируется одним из стандартных распределений А(r)

и соответствующие им fсист ( ) или набором, для которых известны ряд таких функций.

159

Оптимальные соотношения параметров в ЛА и ЗА.

Параметры: ширина ДН облучателя - 2 , фокусное расстояние f ,

размер раскрыва антенны α, угол раскрыва 2Ψ0 .

Для определения оптимального соотношения параметров апертурных Л и

З антенны рассчитываем KHД параболоида вращения. KHДрассчитывается исходя из общего определения

амплитуда поля центрального излучателя Гюйгенса Множитель системы определяется соотношением (10.23). Полагая в этом

r 2 ftg 2 ), находим

160

Таким образом, получим

Амплитуда поля изотропной антенны

Используя (4.23) и (4.24) имеем

где S0 r02 - площадь раскрыва.

Отсюда для коэффициента использования площади имеем