Fiz_metod_isledov_metal_i_splav

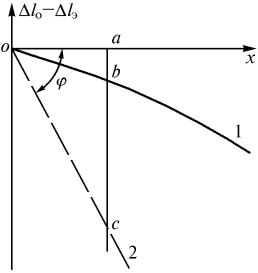
ным погрешностям определения температур характерных точек дилатограммы.

Градуировка дилатометра заключается в определении увеличения по осям координат и построении температурной шкалы.

Выберем произвольную точку b на дилатограмме нагрева образца (рис. 3.6).

соответственно; lo – начальная длина образца, эталона и кварцевой трубки на длине образца);

Значения ∆э −∆к в зависимости от температуры известны (табл. 3.2). Величину tgϕ находят экспериментально, записав расширение эталона в па-

Таблица 3.2

Фрагмент температурной зависимости ∆э−∆к

Для определения ас в дилатометр должны быть установлены эталон и кварцевый стерженек вместо образца. Очевидно, что это можно совместить с определением tgϕ . Соотношение (3.22) позволяет проверить пра-

вильность установки регулировочных винтов подвижного зеркальца.

Для определения температуры любой точки дилатограммы применяют специальные линейки. Зная kx и, пользуясь данными табл. 3.2, вычис-

ляют оа по уравнению (3.19) для 100, 200, 300 °С и так далее, и получают искомую линейку. Например, для определения температуры, соответствующей точке b дилатограммы (см. рис. 3.6), линейку располагают параллельно оси х на уровне точки b и совмещают с осью у деление линейки, соответствующее комнатной температуре. Ответ читается на линейке против точки b.

Ординату заданной точки дилатограммы, например, точки b на рис. 3.6,

находят из выражений (3.20) и (3.21) как алгебраическую сумму:

Это означает, что ордината любой точки дилатограммы не зависит от изменения длины кварцевых трубок, определяется только разностью изменений длин образца и эталона. Выражение (3.24) можно записать иначе:

y = ky (∆o −∆э )lo = ky (∆lo −∆lэ )= ky (lo t1 −lo )−(lэt −lo ) .

Следовательно,

Последнее соотношение не имеет практического значения, так как описанная выше измерительная головка SN регистрирует не длины образца и эталона, а разность их изменения.

Разновидности измерительных регистрирующих головок

Рассмотренная выше головка SN с расположением опор основания зеркальца, показанным на рис. 3.5,б, предназначена для записи дифференциальных дилатограмм, по ординате которых откладываются разность изменений длин образца и эталона. Такая головка удобна при определении температурных интервалов фазовых превращений. Применяются также головки, аналогичные по конструкции SN, но обладающие бόльшим увеличением по одной или обеим осям.

42

Вычисляя αo , необходимо учитывать знак производной dy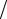dx . Кроме то-

го, следует иметь в виду, что резкое изменение хода дилатометрической кривой обусловлено не температурной зависимостью коэффициента расширения, а объемным эффектом фазового превращения.

Определение среднего коэффициента термического расширения в интервале температур. Обозначим через z1 и z2 отрезки вертикальных прямых, заключенные между дилатограммой образца и линией расширения эталона (рис. 3.9).

В соответствии с уравнением (3.21)

Оценка дилатометрического эффекта фазового превращения

Пусть в сплаве при нагреве происходит фазовое превращение, сопровождающееся уменьшением объема (рис. 3.10). В результате превращения коэффициент линейного расширения образца изменяется от αн до αк .

В случае отсутствия превращения и неизменности αн при нагреве до tк

световой «зайчик» оказался бы в точке е – на продолжении участка оа дилатограммы.

Если допустить, что при отсутствии превращения в точке а произошло бы скачкообразное изменение коэффициента расширения от αн до αк , то при температуре tк

«зайчик» пришел бы в точку b. Отрезок аb параллелен линии hi расширения образца после завершения реального превращения.

По-прежнему допуская, что превращение не происходит или происходит с нулевым объемным эффектом, но считая, что коэффициент расширения образца изменяется так, как это происходит в действительности, то есть постепенно возрастает в интервале температур

tнKtк от αн до αк , получим, что «зайчик» должен перемещаться по кри-

вой ad. Точка d должна лежать на середине отрезка bе. На самом деле при температуре tк «зайчик» оказывается в точке h. Следовательно, отрезок dh

и есть дилатометрический эффект фазового превращения.

Величину дилатометрического эффекта можно найти иначе, более простым способом. Для этого участок оа дилатограммы, предшествующий превращению, следует продолжить до температуры конца превращения, то есть до точки е. Участок дилатограммы hi, соответствующий нагреву после окончания превращения, продолжить до температуры начала последнего – до точки f. Нетрудно убедиться, что отрезок gc, соединяющий середины отрезков ае и fh, равен отрезку dh. Таким образом gc – дилатометрический эффект превращения.

Рассмотренный способ определения дилатометрического эффекта превращения базируется на допущении, что шкала температуры, откладываемая по оси х, равномерна. В действительности это не так, поскольку температурная зависимость коэффициента расширения пироса нелинейна. Но так

45

как температурные интервалы фазовых превращений обычно не слишком велики, неравномерностью температурной шкалы можно пренебречь.

Величина дилатометрических эффектов превращений в стали существенно зависит от содержания углерода. Образование аустенита при нагреве сопровождается тем меньшим линейным эффектом, чем выше содержание углерода в стали (рис. 3.11).

Рис. 3.11. Фрагменты дилатограмм нагрева железа и углеродистых сталей 20, 40, У8 (а) и зависимость дилатометрического эффекта образования аустенита от содержания углерода в стали (б)

Это обусловлено увеличением удельного объема аустенита при повышении содержания углерода в нем и, следовательно, уменьшением разности

Влияние некоторых факторов на дилатограммы

1.Выше уже отмечалось, что применение эталона избавляет от необходимости использовать термопары для записи температуры. Но при этом нельзя забывать, что по дилатограмме определяется температура эталона, а не образца. Например, во время протекания изотермического превращения в образце температура эталона продолжает повышаться. Следовательно, изотермические превращения на дилатограммах растягиваются на интервал температур. В начале превращения температуры образца и эталона одинаковы, а в конце могут значительно различаться. При нагреве эвтектоидной углеродистой стали со скоростью 800…1000 К/ч в конце образования аустенита температура эталона выше температуры образца на 15…20 °С.

2.Форма дилатограммы даже стабильного материала может значительно искажаться при увеличении скорости нагрева или охлаждения. Например, дилатограммы медленного и быстрого нагрева заэвтектоидной углеродистой стали (рис. 3.13) резко различны в температурной области максимального различия скоростей нагрева (ниже Ac1).

Повышение скорости охлаждения в субкритическом интервале температур после завершения превращения аустенита также вызывает существенное искажение дилатограммы (см. рис. 3.13,а). Эти искажения обусловлены различием тепловых свойств образца и эталона из пироса (сплав на основе никеля – см. раздел 3.2.3). Наиболее значительно различается теплопроводность железа и никеля – по-

следняя больше, чем теплопровод-

ность железа на 20…40 % в зави- Рис. 3.13. Дилатограммы заэвтектоидной

углеродистой стали: а – медленный на- симости от температуры. Это долж- грев (начальная температура печи 20 °С),

но приводить к более быстрому охлаждение до 430 °C с печью, далее на

изменению средней температуры воздухе; б – быстрый нагрев (начальная

эталона и, следовательно, его дли- температура печи 650 °C), охлаждение на ны при ускоренном нагреве или воздухе

охлаждении, чем стального образца, что и отображено на дилатограммах, приведенных на рис. 3.13.

3. Влияние скорости изменения температуры на дилатограмму наиболее существенно проявляется при охлаждении стальных образцов в интервале протекания фазовых превращений. С ускорением охлаждения темпе-

47

ратурный интервал диффузионного превращения расширяется и смещается в область более низких температур (см. рис. 3.13). При охлаждении с печью эвтектоидное превращение аустенита происходило в интервале 700…665 °С, а при охлаждении на воздухе – в интервале 660…550 °С. Кроме того, с ускорением охлаждения наблюдается значительное увеличение дилатометрического эффекта превращения. Это нельзя объяснить изменением структуры, происходящим при ускоренном охлаждении. Причиной увеличения дилатометрического эффекта является разогрев образца теплотой превращения. Напомним, что температуры характерных точек дилатограммы определяются по эталону, а действительная температура образца может более или менее отличаться от найденной по дилатограмме. При охлаждении с печью эвтектоидное превращение происходило при почти постоянной температуре, а не в области 700…665 °С, что легко подтверждается путем записи температуры образца с помощью приваренной к нему термопары и электронного потенциометра. Следовательно, к концу распада аустенита температура образца оказывается более высокой, чем она была бы при отсутствии теплового эффекта. Вследствие этого и длина образца оказывается чуть больше. При дальнейшем охлаждении теплота превращения рассеивается, а длина образца несколько уменьшается. Эталон во время превращения в образце охлаждается равномерно. В результате на дилатограмме появляется пик (на рис. 3.13,а – при 665 °С), обусловленный тепловым эффектом превращения.

Высоту пика ∆h на дилатограмме можно рассчитать по уравнению

lo =50 мм – начальная длина образца (см. раздел 3.2.4), α =16 10−6 1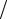°С –

средний коэффициент расширения образца в интервале превращения, ∆t = 20°C – разогрев образца тепловым эффектом. При указанных значени-

ях величин получаем ∆h =5,1 мм. На дилатограмме ∆h = 6 мм, что можно

считать хорошим согласованием расчетных и экспериментальных данных. Разогрев образца тепловым эффектом превращения при охлаждении

на воздухе составляет около 65 °С, так как при ускоренном охлаждении теплота превращения не успевает рассеиваться. Расчет высоты пика на дилатограмме по уравнению (3.34) дает ∆h =16,6 мм, ∆h на дилатограмме –

около 21 мм.

Полученное расхождение может быть обусловлено трудностью точного определения ∆h графическим способом по рис. 3.13,б, а также тем, что расчет не учитывает тепловых свойств образца и эталона.

48

3.2.7. Совмещение дилатометрии с термическим анализом

Выше было показано, что при записи дифференциальных дилатограмм температуры образца и эталона в некоторые моменты времени могут существенно различаться. Очевидно, что это может привести к неправильному истолкованию результатов опытов. Для предотвращения такого рода ошибок следует одновременно с записью дилатограммы регистрировать температуру образца. Это можно сделать, приварив тонкую термопару к образцу и присоединив ее к самопишущему прибору, например, к электронному автоматическому потенциометру. Таким образом, одновременно будут записаны дилатограмма и термограмма одного и того же образца. Пример такого совмещения дилатометрии и термического анализа приведен на рис. 3.14.

Рис. 3.14. Одновременно записанные термограмма (а) и дилатограмма (б) заэвтектоидной стали. Скорость нагрева перед началом образования аустенита ~20 °С/c; скорость охлаждения на воздухе от температуры нагрева до начала перлитного превращения ~385 °С/с

Температуры характерных точек дилатограммы и термограммы различаются в той или иной степени. Температура начала образования аустенита при нагреве соответственно составляет 715 и 720 °С, температура нагрева – 825 и 832 °С. Различие дилатометрической и термографической температур этих точек почти одинаково – 5…7 градусов, что в большинстве

49

случаев допустимо. Несоответствие температур конца образования аустенита составляет уже 20 ° (755 и 735 °С). Расхождение температур начала перлитного превращения при охлаждении равно 22 °С (643 и 665 °С). Приведенный пример показывает, что температура образца в различные моменты времени может быть как выше, так и ниже температуры эталона.

Анализ одновременно записанных дилатограмм и термограмм при различных скоростях нагрева и охлаждения показывает, что расхождение дилатометрических и термографических температур тем больше, чем выше скорость изменения температуры. Более или менее достоверная оценка температуры образца по дилатограмме возможна только при медленном нагреве и охлаждении с печью. В остальных случаях температуру образца следует определять с помощью приваренной к нему термопары.

3.2.8. Некоторые применения дилатометрии

Определение энергии активации изотермического процесса

Энергия активации изотермического процесса может быть найдена путем анализа серии дилатограмм, записанных при различных температурах. Для записи изменения длины образца при постоянной температуре применяют подвижную кассету, устанавливая ее вместо матового стекла. Кассета с фотопластинкой медленно перемещается в горизонтальном направлении с помощью электрического двигателя с редуктором. В результате разность изменения длин образца и кварцевой трубки записывается в зависимости от времени при постоянной температуре.

Скорость превращения, протекающего диффузионным путем, экспоненциально зависит от температуры. Так как скорость изменения объема и длины определяется скоростью превращения, то

Здесь А – константа, Q – энергия активации процесса, R – газовая постоянная (в системе СИ R = 8,31·103 Дж/моль·К). Логарифмируя выражение (3.35), получаем

Последнее уравнение описывает прямую в координатах ln ∆∆τl − T1 , что по-

зволяет определить А и Q.

Получив серию дилатограмм при различных температурах (рис. 3.15,а), задают некоторое фиксированное значение ∆l , заключенное между двумя прямыми, параллельными оси абсцисс. Это значение ∆l достигается за время ∆τ1 > ∆τ2 > ∆τ3 > ∆τ4 при температурах T1 <T2 <T3 <T4 соответственно.

50