
Bitner_V_A_-_Kratky_kurs_shkolnoy_matematiki
.pdf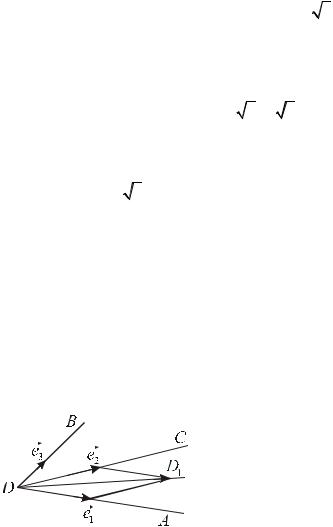
Краткий курс школьной математики |
341 |
|
|
1)n CD = p, CB = q, CS = r, SA = SB = SC = SD = AB = a .
2)SAB - равносторонний (по условию)
(SA, AB) = 1800 − SAB = 1800 − 600 = 1200 .
3)Аналогично, (SA, BS ) = 1200 .
4)(SA, SC ) = ASC = 1800 − 2 SCA , где SCA = (CA, CS ) = ϕ .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда cosϕ = |
|
CA CS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
, где |
CS |
= a, |
CA |
= a |
2, CA = p + q , тогда |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CA |
CS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
CA CS = |
( p + q )r = pr + qr = |
p |
|
r |
cos 600 + |
q |
|
r |
cos 600 |
= |
|
||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
a |
|
+ |
|
a |
= a2 , тогда cosϕ = |
|
|
|
a |
|
|
|
|
|
= |
,ϕ = 450 . |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a a |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SC BD |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
5) n (SC, BD) |
= ϕ1 , тогда cosϕ1 = |
|
|
|
|
|
|
|
|
, где |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SC |
|
BD |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
SC |
|
= a, |
BD |
= a |
|
2, SC = −r, BD = p − q , тогда |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
SC BD = −r ( |
p − q ) = −r p + r q = − |
r |
|
|
p |
cos 600 + |
r |
|
q |
cos 600 = |
|
|||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
− |
a |
|
+ |
a |
|
= 0 SC BD и (SC, BD) = 900 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: а) 1200 ; б) 1200 ; в) 450 ; г) 900 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Задача 5. Даны три луча DA, DB и DC , не лежащие в одной плоско- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
сти. Известно, |
|
что |
ADB + BDC = 1800 . |
Докажите, что |
луч |
||||||||||||||||||||||||||||||||||||||||||||||||
DB DD1 , где DD1 |
- биссектриса ADC . – см. рис.20. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
Отложим от тч. |
D на данных лу- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чах |
|
единичные |
|
векторы |
e1 , e2 и |
e3 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(имеющие длину 1). |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
рис.20

344 |
В.А.Битнер |
|
|
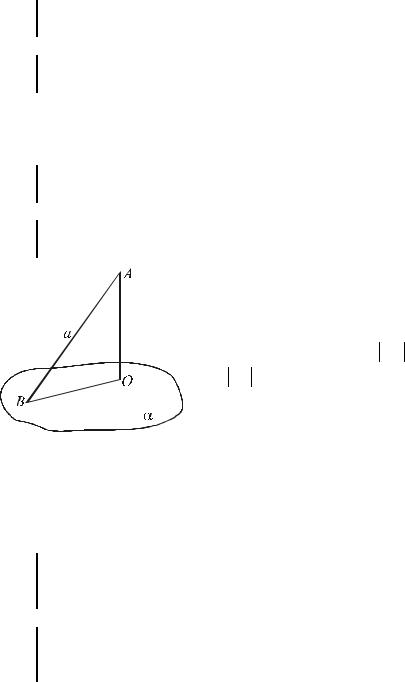
t 13 e две прямые перпендикулярны плоскости, то они параллельны. – см. рис.22.
t 14 e две плоскости перпендикулярны прямой, то они параллельны. – см. рис.23.
(11)Расстояние от точки до плоскости. Угол между наклонной и плоскости.
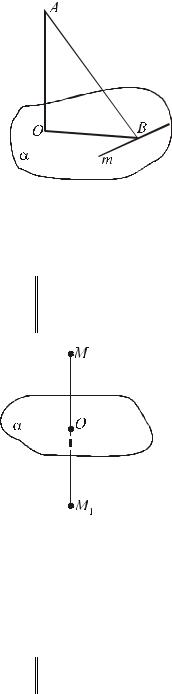
t 15 Расстояние от точки до плоскости равно расстоянию от этой точки до ее проекции на данную плоскость. – см. рис.24.
o 4 Углом между наклонной и плоскостью называют угол между наклонной и ее проекцией на плоскость. – см. рис.24.
1)AO α , то есть O = Прα ( A) , то-
гда AO - расстояние от тч. A до плоскости α . Обозначают AO . e A α ,
то AA = 0 .
2) BO = Прα ( AB) , тогда ABO - угол
прямой AB с плоскостью α . Обозна-
чают: (( AB) ,α ) или (a,α ) .
рис.24
(12)Теорема о трех перпендикулярах.
t 16 e прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. – см.
рис.25.
t 17 e прямая, лежащая в плоскости, перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной. – см.
рис.25.
346 В.А.Битнер
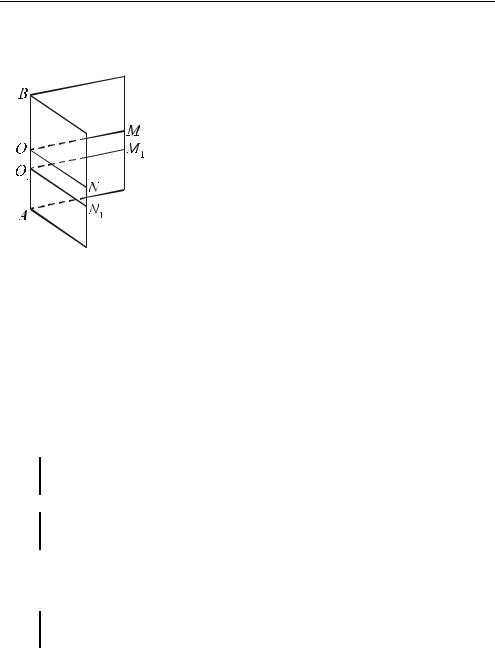
Обозначается двугранный угол: α aβ или α ABβ , или AB , или
a .
Полуплоскости α и β называются гранями двугранного угла, а прямая a - его ребром. Двугранный угол может быть выпуклым и невыпуклым. Выпуклые двугранные углы могут быть прямыми, острыми, тупыми, развернутыми, смежными и вертикальными.
рис.27
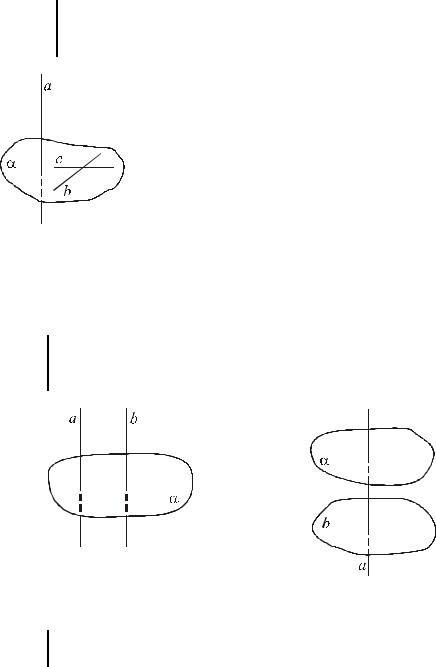
Через произвольную точку O ребра a двугранного угла α aβ проведем плоскость γ , перпендикулярную a . Получим плоский угол MON : MON = γ ∩ α aβ . Величина MON не зависит от выбора точки O на ребре двугранного угла. То есть M1O1 N1 = MON , где
O1 a, O1M1 a, O1M1 α , O1 N1 a, O1 N1 β (O1M || OM , O1 N1 || ON ) -
см. рис.27.
o 7 Пересечение двугранного угла и плоскости, перпендикулярной его ребру, называют линейным углом двугранного угла.
o 8 Величиной двугранного угла называют величину его линейного угла.
Величина двугранного угла принадлежит промежутку (0; 360) .
o 9 Углом между двумя пересекающимися плоскостями называют наименьший из двугранных углов, заданных плоскостями.
Обозначается (α ; β ) = ϕ , где 00 ≤ ϕ ≤ 900 .
Краткий курс школьной математики |
347 |
|
|
(15)Понятие о многогранном угле. Трехгранный угол.
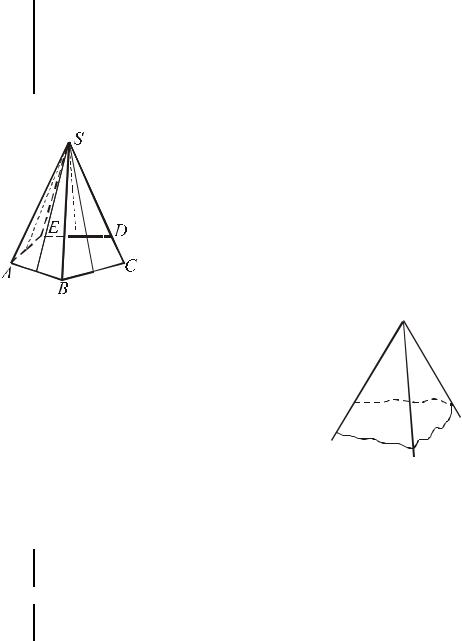
o 10 n дана простая замкнутая плоская ломаная линия ABC...EA и точка S , не принадлежащая ее плоскости. Объединение лучей, имеющих общее начало S и пересекающих данную ломаную, а также одной из образующихся при этом двух пространственных областей называется многогранным углом. – см. рис.28.
Точку S называют вершиной многогранного угла, лучи SA, SB, SC, ..., SE его ребрами, плоские углы ASB, BSC, ...BSE - его гранями. В зависимости от числа граней различают трехгранные, четырехгранные и т.д. углы. Многогранный угол, изображенный на рис.28, обозначают SAB...E . Трехгранный угол (рис.29) обладает замечательными свойствами: в каждом трехгранном угле:
рис.28 |
1) Сумма всех |
S |
плоских углов |
|
|
|
|
|
|
меньше 3600 . То |
|
есть ASB + BSC + ASC < 3600 .
2) Каждый плоский угол меньше суммы
двух других. То есть |
C |
|
|
ASC < ASB + BSC . |
A |
|
B |
|
рис.29 |
(16)Признак перпендикулярности двух плоскостей.
o 11 Две плоскости называются перпендикулярными, если при пересечении они образуют прямые двугранные углы.
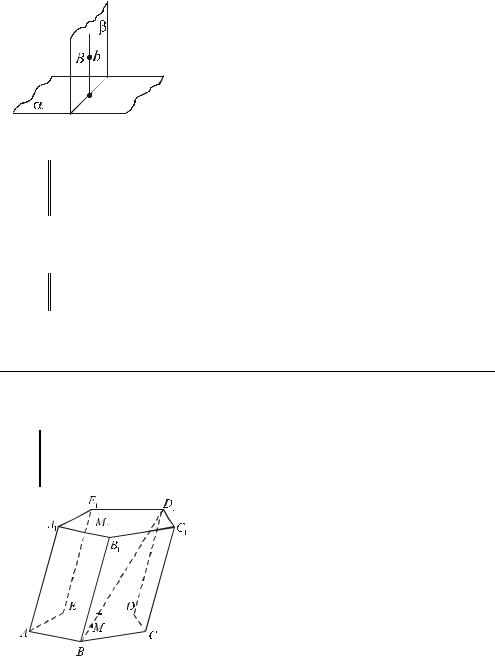
t 18 e плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости. – см. рис.30.
То есть eb β , b α , то β α .
348 |
В.А.Битнер |
|
|
рис.30
t 19 e две плоскости перпендикулярны, и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, то он весь лежит в этой плоскости. – см. рис.30.
То есть eb α , β α , B b, B β , то b β .
t 20 e две пересекающиеся плоскости перпендикулярны третьей, то линия пересечения также перпендикулярна этой плоскости.
Тема III. Многогранники.
(1)Призма.
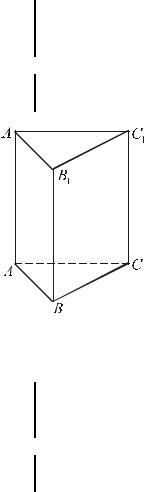
o 1 Многогранник, две грани которого равные многоугольники, лежащие в параллельных плоскостях, а остальные грани – параллелограммы, называется призмой. – см. рис.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначается |
|
ABCDEA B C D E . |
Тч. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A, B,..., E, A , B ,...E - вершины призмы; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB, BC,...AE, AA , BB ,...EE , A B ,...A E |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
ее ребра, |
|
причем, |
|
AA , BB ,..., EE |
- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
боковые ребра; |
пятиугольники ABCDE |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
A B C D E , |
параллелограммы |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ABB A , BCC B ,...AEE A - |
грани |
приз- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
рис.1 |
|
|
мы, причем |
|
ABCDE и A B C D E |
- со- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ответственно нижнее и верхнее основание,
Краткий курс школьной математики |
349 |
|
|
остальные грани – боковые; MM1 |
– высота призмы, где |
||||||
M ( ABC ) , M |
1 |
( A B C ) , MM |
1 |
|
( ABC ) ; BD - диагональ призмы. |
||
|
1 |
1 |
1 |
|
1 |
||
Призмы бывают треугольные, четырехугольные, пятиугольные и т.д.
o 2 e боковое ребро призмы плоскости основания, то призма называется прямой (см. рис.2), остальные призмы – наклонные
(см. рис.1).
o 3 Прямая призма, в основании которой лежит правильный многоугольник, называется правильной (см. рис.2).
ABCA B C - изображение прямой треуголь- |
||
1 |
1 |
1 |
ной призмы. Это может быть и изображением правильной треугольной призмы ( e ABC - изображение правильного треугольника, при-
чем, AA ( ABC ) ).
1
рис.2
o 4 e в основании призмы лежит параллелограмм, то она называется параллелепипедом. Различают прямые и наклонные параллелепипеды (см. рис.3 и 4).
o 5 Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным параллелепипедом.
ABCDA B C D - наклонный параллелепипед, можно обозначать коро- |
|||
1 |
1 |
1 |
1 |
че: AC1 ;
MK1 - прямой параллелепипед, также может быть изображен и прямо-
угольный параллелепипед.
350 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В.А.Битнер |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рис.3 |
рис.4 |
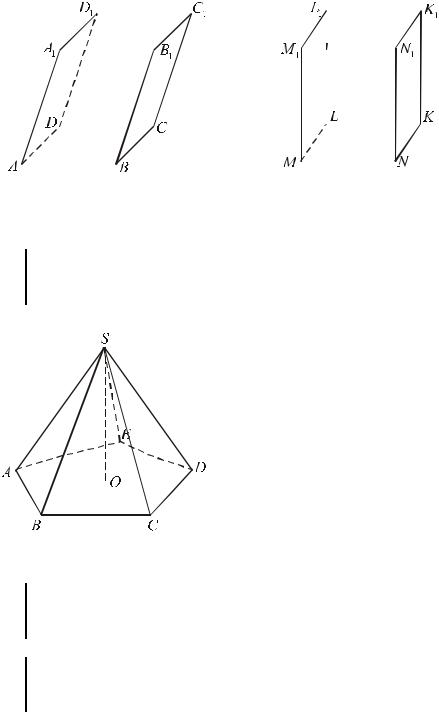
(2)Пирамида.
o 6 Многогранник, одна грань которого многоугольник, а остальные грани – треугольники, имеющие общую вершину, называется пирамидой. – см. рис.5.
Пирамиды бывают треугольные (такая пирамида называется тетраэдром), четырехугольные, пятиугольные и т.д.
SABCDE - пятиугольная пирамида, S - ее вершина, ABCDE - основание; SAB, SBC,..., SAE - боковые грани; SA, SB,..., SE - боковые реб-
ра; SO ( ABC ) , SO - высота пира-
миды.
рис.5
o 7 Пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр основания, называется правильной (см. рис.6 и 7).
o 8 Часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию, называется усеченной пирамидой.


 Зеркальная симметрия является перемещением.
Зеркальная симметрия является перемещением.