
- •I. Первый признак сравнения.
- •II. Второй признак сравнения (признак сравнения в предельной форме).
- •Интегральный признак Коши-Маклорена.
- •Достаточный признак разложимости функции в ряд Тейлора.
- •Приложения степенных рядов.
- •Второй способ решения дифференциального уравнения.
- •III. Применение степенных рядов для приближенного вычисления значений функций.
- •Связь комплексной формы ряда Фурье с комплексным гармоническим колебанием.
- •Спектральные характеристики комплексной формы ряда Фурье.
- •Понятие интеграла от фкп.
- •Ряд Лорана.
Ряд Лорана.
Т-ма: Если
ФКП
 однозначная аналитическая функция в
кольце
однозначная аналитическая функция в
кольце
 ,
то в этом кольце функция однозначно
разложена в ряд Лорана
,
то в этом кольце функция однозначно
разложена в ряд Лорана
 ,
,
 ,
где
,
где - любой замкнутый контур, лежащий внутри
кольца аналитичности, ориентированный
против часовой стрелки.
- любой замкнутый контур, лежащий внутри
кольца аналитичности, ориентированный
против часовой стрелки.
Доказательство:
 аналитическая в кольце. Рассмотрим
кольцо
аналитическая в кольце. Рассмотрим
кольцо
 ,
лежащее внутри кольца аналитичности.
,
лежащее внутри кольца аналитичности.
 ,
тогда в силу теоремы функция
,
тогда в силу теоремы функция
 будет аналитической внутри построенного
кольца, включая границу. В построенном
кольце проведем разрез
будет аналитической внутри построенного
кольца, включая границу. В построенном
кольце проведем разрез
 ,
чтобы превратить его в односвязную
область. Согласно интегральной формуле
Коши для односвязной области, ограниченной
,
чтобы превратить его в односвязную
область. Согласно интегральной формуле
Коши для односвязной области, ограниченной
 и любой точкой
и любой точкой
 из
этой области имеем
из
этой области имеем

 для
функции
для
функции

внутри вспомогательного кольца имеет место представление:

Преобразуем
интегралы
 и
и
 ,
входящие в представление функции
,
входящие в представление функции
 .
.

Подынтегральная
функция


Полученный
ряд сходится абсолютно и равномерно
внутри вспомогательного круга, т.к.
 мы можем подставить этот ряд под интеграл
мы можем подставить этот ряд под интеграл
 и поменять знак суммы и интеграла
местами, т.к. равномерно сходящиеся ряды
можно почленно интегрировать.
и поменять знак суммы и интеграла
местами, т.к. равномерно сходящиеся ряды
можно почленно интегрировать.

Вводя вспомогательное обозначение

Имеем

Преобразуем
 .
.

 ,
,



Сменим индекс суммирования в последней сумме



Подставим
полученный равномерно сходящийся ряд
в интеграл
 и поменяем
и поменяем
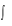 и
и
 местами.
местами.

Подставим
 и
и
 в
представление функции
в
представление функции





Поскольку
интеграл от аналитической функции не
зависит от контура интегрирования можно
вместо
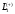 и
и
 взять любой контур, лежащий внутри
кольца аналитичности и ориентированный
против часовой стрелки
взять любой контур, лежащий внутри
кольца аналитичности и ориентированный
против часовой стрелки
 для
для

Пример:
Найти все разложения в ряд Лорана по
степеням
 у функции:
у функции:



Области разложения в ряд Лорана.
Особые
точки:








Вывод:


Ответ:



