
- •I. Первый признак сравнения.
- •II. Второй признак сравнения (признак сравнения в предельной форме).
- •Интегральный признак Коши-Маклорена.
- •Достаточный признак разложимости функции в ряд Тейлора.
- •Приложения степенных рядов.
- •Второй способ решения дифференциального уравнения.
- •III. Применение степенных рядов для приближенного вычисления значений функций.
- •Связь комплексной формы ряда Фурье с комплексным гармоническим колебанием.
- •Спектральные характеристики комплексной формы ряда Фурье.
- •Понятие интеграла от фкп.
- •Ряд Лорана.
Понятие интеграла от фкп.
Пусть
 - кривая в комплексной плоскости, заданная
параметрически:
- кривая в комплексной плоскости, заданная
параметрически:
 ,
,
эта кривая удовлетворяет двум условиям:
1) Она кусочно-гладкая
2) Спрямляемая, т.е. имеет определенную длину.
В каждой
точке этой кривой определена ФКП
 .
.
Введем
понятие интеграла от ФКП
 по кривой
по кривой
 ,
т.е.
,
т.е.
 .
.
Для этого проведем ряд вспомогательных построений.
Шаг №1.
Разобьем кривую
 на
на
 частичных дуг точками
частичных дуг точками



Шаг №2. На
каждой из частичных дуг
 выберем произвольную точку
выберем произвольную точку

 и вычислим
и вычислим
 в этих точках, т.е.
в этих точках, т.е.
 .
.
Шаг №3.
Составим .
Указанная сумма зависит от способа
разбиения дуги
.
Указанная сумма зависит от способа
разбиения дуги на частичные дуги и от выбора точек
на частичные дуги и от выбора точек
 .
.
Шаг №4.
Рассмотрим всевозможные разбиения дуги
 на частичные дуги, такие, что
на частичные дуги, такие, что
 .
.
Это означает,
что разбиение дуги равномерно мелкое
и при этом
 .
.
Опр.:
Интегралом от ФКП по дуге
 называется предел интегральных сумм,
построенных в шаге №3, найденных при
условии шага №4.
называется предел интегральных сумм,
построенных в шаге №3, найденных при
условии шага №4.

Если
указанный предел существует и конечен,
и не зависит от способа разбиения дуги
на частичные дуги, и от выбора точки
 ,
то говорят, что
,
то говорят, что
 интегрируема по дуге
интегрируема по дуге
 .
.
Вычисление интеграла от ФКП.
Интеграл от ФКП может быть вычислен тремя способами:
1) сведением к двум криволинейным интегралам второго рода;
2) сведением к определенному интегралу по параметру;
3) по формулам Ньютона-Лейбница в случае аналитичности функции.
Эти формулы имеют вид:

I. Сведение интеграла от ФКП к двум криволинейным интегралам второго рода.
Пусть
 .
Воспользуемся определением интеграла
от функции комплексного переменного.
.
Воспользуемся определением интеграла
от функции комплексного переменного.




Поскольку интеграл от ФКП свелся к двум криволинейным интегралам второго рода, то все свойства криволинейного интеграла второго рода сохраняются и для интеграла от ФКП.
Свойства интеграла от ФКП.
 Интеграл от ФКП зависит от направления
дуги интегрирования.
Интеграл от ФКП зависит от направления
дуги интегрирования.

 Интеграл по дуге
Интеграл по дуге






 Если
Если
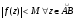
 ,
где
,
где
 - длина дуги
- длина дуги
 .
.
Доказательство:

Замечание:
Из доказательства ясно, что
 - длина дуги
- длина дуги
 .
.
II. Сведение интеграла от ФКП к определенному интегралу по параметру.
Если в
формуле
 вычислить криволинейные интегралы с
учетом параметрического задания кривой
вычислить криволинейные интегралы с
учетом параметрического задания кривой
 ,
,
то придем к двум определенным интегралам по параметру.

 .
.
Интегральная теорема Коши для односвязной области.
Т-ма: Если
 однозначная аналитическая в некоторой
односвязной области
однозначная аналитическая в некоторой
односвязной области
 функция, то интеграл от этой функции по
любимому замкнутому контуру, лежащему
внутри этой области, равен нулю.
функция, то интеграл от этой функции по
любимому замкнутому контуру, лежащему
внутри этой области, равен нулю.
 .
.
Доказательство: Воспользуемся сведением интеграла от ФКП к двум криволинейным интегралам второго рода:

Для их вычисления воспользуемся формулой Грина:
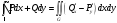


Воспользуемся
тем, что функция
 является аналитической в
является аналитической в

 для нее выполняются условия Коши-Римана:
для нее выполняются условия Коши-Римана:

 .
.
Обобщение интегральной теоремы Коши для односвязной области.
Т-ма: Если
ФКП
 однозначная, аналитическая в односвязной
области
однозначная, аналитическая в односвязной
области
 и непрерывная на границе этой области,
то интеграл по границе этой области,
ориентированный против часовой стрелки,
равен нулю.
и непрерывная на границе этой области,
то интеграл по границе этой области,
ориентированный против часовой стрелки,
равен нулю.
 (без доказательства).
(без доказательства).
Интегральная теорема Коши для многосвязной области.
Если ФКП
 аналитическая в многосвязной области
аналитическая в многосвязной области
 ,
ограниченной вне контуром
,
ограниченной вне контуром
 ,
ориентированном против часовой стрелки
и изнутри контурами
,
ориентированном против часовой стрелки
и изнутри контурами
 ,
ориентированными по часовой стрелке,
непрерывная на границе функция, то
интеграл по полной границе этой области
равен нулю, т.е.
,
ориентированными по часовой стрелке,
непрерывная на границе функция, то
интеграл по полной границе этой области
равен нулю, т.е.

Доказательство:
Воспользуемся
обобщением интегральной теоремы Коши
для односвязной области. Проведем
разрезы
 и
и
 ,
,
 ,
превращающие нашу многосвязную область
в односвязную.
,
превращающие нашу многосвязную область
в односвязную.
В силу обобщения интеграл по полной границе, построенной односвязной области равен нулю, т.е.

Учтем, что


Замечание: Интегральную теорему Коши для многосвязной области иногда записывают в виде

Независимость от пути интегрирования интеграла от аналитической в области функции.
Т-ма: Пусть
 - аналитическая в односвязной области
- аналитическая в односвязной области
 функция, тогда интегралы по любым путям,
соединяющих две любые точки этой области,
целиком лежащих в ней, равны между собой,
т.е. интеграл не зависит от пути
интегрирования.
функция, тогда интегралы по любым путям,
соединяющих две любые точки этой области,
целиком лежащих в ней, равны между собой,
т.е. интеграл не зависит от пути
интегрирования.

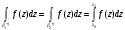
 - как интеграл по замкнутому контуру,
целиком лежащему в области аналитичности
функции.
- как интеграл по замкнутому контуру,
целиком лежащему в области аналитичности
функции.
(теорема Коши для односвязной области)


Понятие определенного интеграла с переменным верхним пределом для аналитической функции.
Опр.:
Определенным интегралом с переменным
верхним пределом для аналитической в
односвязной области
 функции комплексного переменного
функции комплексного переменного
 называется
интеграл вида:
называется
интеграл вида:
 ,
где
,
где
 - некоторая фиксированная точка из
области
- некоторая фиксированная точка из
области
 ,
а
,
а
 - произвольная точка из области
- произвольная точка из области
 .
.
 - аналитическая в области
- аналитическая в области
 .
.
Замечание:
 означает, что интеграл берется по любому
контуру, лежащему в области
означает, что интеграл берется по любому
контуру, лежащему в области
 ,
т.к. интеграл от аналитической функции
не зависит от пути интегрирования.
,
т.к. интеграл от аналитической функции
не зависит от пути интегрирования.
Теорема об аналитичности определенного интеграла с переменным верхним пределом.
Т-ма: Если
 однозначная аналитическая в односвязной
области
однозначная аналитическая в односвязной
области
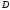 функция,
то ее определенный интеграл с переменным
верхним пределом является аналитической
функцией в этой области.
функция,
то ее определенный интеграл с переменным
верхним пределом является аналитической
функцией в этой области.
Доказательство:

Выражения, стоящее под знаком криволинейных интегралов II рода, являются полными дифференциалами, т.к.
 если
если

Действительно,



 Выполняется т.к.
Выполняется т.к.
 аналитическая
аналитическая


 К.Р.
К.Р.
 аналитическая.
аналитическая.

Найдем
 ,
,
 ,
,
 ,
,
 и проверим условия Коши-Римана. Поскольку
и проверим условия Коши-Римана. Поскольку

Эти функции
непрерывны для
 ,
т.к.
,
т.к.
 непрерывны
в силу аналитичности
непрерывны
в силу аналитичности
 .
.

 непрерывные функции в силу аналитичности
функции
непрерывные функции в силу аналитичности
функции
 .
.


Вывод:
Условие Коши-Римана выполняется для
 из области
из области
 функция
функция
 является
аналитической.
является
аналитической.
Опр.:
Первообразной для аналитической функции
 в односвязной области
в односвязной области
 называется
аналитическая функция
называется
аналитическая функция
 в области
в области
 ,
такая, что
,
такая, что
 .
.
Т-ма:
Определенный интеграл с переменным
верхним пределом является первообразной
для функции
 .
.
Доказательство:
Ранее было доказано, что функция
 является аналитической в области
является аналитической в области
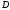 .
Найдем
.
Найдем
 .
.
Теорема о структуре всех первообразных.
Т-ма: Если
ФКП
 является аналитической в области
является аналитической в области
 и
и
 и
и
 какие-либо две первообразные для этой
функции, то
какие-либо две первообразные для этой
функции, то
 .
.
Доказательство:
Введем в рассмотрение вспомогательную
функцию комплексного переменного
 .
Найдем
.
Найдем
 .
.
Если
 ,
то
,
то


Известно,
что
 аналитическая функция, тогда выполняется
условие Коши-Римана:
аналитическая функция, тогда выполняется
условие Коши-Римана:


Имеем






Формула Ньютона-Лейбница для аналитической в односвязной области функции.
Т-ма: Если
функция
 аналитическая в односвязной области
аналитическая в односвязной области
 и
и
 -
какая-либо первообразная для этой
функции, то для
-
какая-либо первообразная для этой
функции, то для
 имеет место формула Ньютона-Лейбница.
имеет место формула Ньютона-Лейбница.

Доказательство:
Так как
 - первообразная (из дано) и
- первообразная (из дано) и
 -
определенный интеграл с переменным
верхним пределом также первообразная,
то в силу теоремы о структуре всех
первообразных имеем
-
определенный интеграл с переменным
верхним пределом также первообразная,
то в силу теоремы о структуре всех
первообразных имеем





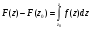



Интегральная формула Коши и ее обобщения.
Т-ма: Если
 однозначная аналитическая функция в
односвязной области
однозначная аналитическая функция в
односвязной области
 и непрерывная на границе этой области,
то для нее справедлива интегральная
формула Коши.
и непрерывная на границе этой области,
то для нее справедлива интегральная
формула Коши.

Доказательство:
Пусть
 ,
введем вспомогательную функцию:
,
введем вспомогательную функцию:
 - аналитическая в области
- аналитическая в области
 (т.к.
(т.к.
 - аналитическая для
- аналитическая для
 ,
,
 - аналитическая для
- аналитическая для
 )
)
 - аналитическая в области
- аналитическая в области
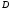 ,
непрерывная на границе. В силу обобщения
интегральной теоремы Коши для односвязной
области
,
непрерывная на границе. В силу обобщения
интегральной теоремы Коши для односвязной
области

Пусть
 .
.
 - аналитическая в области
- аналитическая в области
 за
исключением точки
за
исключением точки
 .
Вырежем эту точку из области
.
Вырежем эту точку из области
 с помощью окружности
с помощью окружности
 ,
лежащей в этой области.
,
лежащей в этой области.
Рассмотрим
область
 ,
которая получена из области
,
которая получена из области
 выбрасыванием круга
выбрасыванием круга
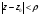 .
Это многосвязная область, в которой
функция
.
Это многосвязная область, в которой
функция
 является аналитической, тогда в силу
интегральной теоремы Коши для многосвязной
области имеем
является аналитической, тогда в силу
интегральной теоремы Коши для многосвязной
области имеем




Чтобы
вычислить интеграл для области
 надо перейти к пределу при
надо перейти к пределу при
 ,
тогда
,
тогда

Обобщение интегральной формулы Коши.
Т-ма: Если
 однозначная аналитическая функция
комплексного переменного в односвязной
области
однозначная аналитическая функция
комплексного переменного в односвязной
области
 и непрерывная на ее границе, имеет место
обобщение интегральной формулы Коши
и непрерывная на ее границе, имеет место
обобщение интегральной формулы Коши

Доказательство следует из интегральной формулы Коши путем ее дифференцирования.
Комплексные числовые ряды.
Опр.: Комплексным числовым рядом называется аналитическое выражение вида

Опр.: Частичной суммой комплексного числового ряда называется сумма его первых n-слагаемых

Опр.: Комплексный числовой ряд называется сходящимся, если существует и конечен предел последовательности его частичных сумм.
Теорема о связи сходимости комплексного числового ряда и действительного числового ряда.
Т-ма: Для
того, чтобы комплексный числовой ряд
 сходился, необходимо и достаточно, чтобы
сходились действительные числовые ряды
сходился, необходимо и достаточно, чтобы
сходились действительные числовые ряды
 и
и
 .
(Доказательство очевидно).
.
(Доказательство очевидно).
Вывод: Все теоремы, сформулированные для действительного числового ряда, переходят в аналогичной формулировке для комплексного числового ряда.
Опр.:
Комплексный числовой ряд
 называется абсолютно-сходящимся, если
сходится ряд, состоящий из модулей его
членов.
называется абсолютно-сходящимся, если
сходится ряд, состоящий из модулей его
членов.
Опр.: Рядом ФКП называется аналитическое выражение вида
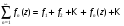 ,
где
,
где
 - ФКП, определенная в некоторой общей
области
- ФКП, определенная в некоторой общей
области

Понятие
поточечной сходимости, равномерной
сходимости и критерий Вейерштрасса
полностью аналогично как для функционального
ряда действительных членов, только
 нужно заменить на
нужно заменить на
 .
.
Опр.: Степенным рядом комплексного переменного называется ряд вида

его радиусом сходимости называется


Аналогично вводятся теорема Абеля и ряд Тейлора:

