
- •I. Первый признак сравнения.
- •II. Второй признак сравнения (признак сравнения в предельной форме).
- •Интегральный признак Коши-Маклорена.
- •Достаточный признак разложимости функции в ряд Тейлора.
- •Приложения степенных рядов.
- •Второй способ решения дифференциального уравнения.
- •III. Применение степенных рядов для приближенного вычисления значений функций.
- •Связь комплексной формы ряда Фурье с комплексным гармоническим колебанием.
- •Спектральные характеристики комплексной формы ряда Фурье.
- •Понятие интеграла от фкп.
- •Ряд Лорана.
Связь комплексной формы ряда Фурье с комплексным гармоническим колебанием.
Теорема:
Функция
 разложена в ряд Фурье. Запишем его
комплексную форму.
разложена в ряд Фурье. Запишем его
комплексную форму.


Воспользуемся формулами связи вещественной и комплексной формы ряда Фурье, а также выражением коэффициентов вещественной формы ряда Фурье через амплитуды и фазы.


Тогда

Очевидно:

Введем вспомогательные обозначения:

Тогда с учетом введенных обозначений имеем


С учетом введенных обозначений, получили единую формулу:
 ,
т.о. ряд Фурье в комплексной форме
принимает вид
,
т.о. ряд Фурье в комплексной форме
принимает вид
 - комплексное гармоническое колебание.
Ряд
Фурье в комплексной форме представляет
собой сумму комплексных гармоник с
амплитудами
- комплексное гармоническое колебание.
Ряд
Фурье в комплексной форме представляет
собой сумму комплексных гармоник с
амплитудами
 ,
фазами
,
фазами
 ,
частотами
,
частотами
 .
.
Спектральные характеристики комплексной формы ряда Фурье.
Выделяют 7 основных спектральных характеристик комплексной формы ряда Фурье:
1) Частотные спектры
2) Линейчатые спектры
3) АЧ спектр (АЧХ)
4) ФЧ спектр (ФЧХ)
5)Спектральная плотность
6) Амплитудный спектр
7) Фазовый спектр
I. Частотные спектры.
Опр.:
Частотными спектрами комплексной формы
ряда Фурье называют числовые
последовательности
 и
и
 ,
,

Замечание: Отрицательных частот в жизни не существует, они являются абстрактным математическим обобщением.
II. Линейчатые спектры.
Опр.: Линейчатыми спектрами комплексной формы ряда Фурье называют числовые последовательности




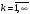
Линейчатые спектры комплексной формы ряда Фурье четно-симметричны.
III. Амплитудно-частотный спектр.
Опр.:
Амплитудно-частотным спектром комплексной
формы ряда Фурье называется числовая
последовательность


Спектр четно-симметричен.
IV. ФЧХ.
Опр.:
Фазово-частотным спектром комплексной
формы ряда Фурье называется числовая
последовательность
 .
.
ФЧХ нечетно-симметрична.
V. Спектральная плотность (функция).
Опр.:
Спектральной плотностью
 комплексной формы ряда Фурье называется
отношение комплексной амплитуды
комплексной формы ряда Фурье называется
отношение комплексной амплитуды
 к приращению частоты
к приращению частоты
 ,
т.к.
,
т.к.

Формула для нахождения спектральной плотности.



Если воспользоваться комплексной формой записи формул Эйлера-Фурье:

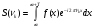
Замечание:
График
 на плоскости построить невозможно,
поскольку для ее изображения нужны три
координатные оси, т.к.
на плоскости построить невозможно,
поскольку для ее изображения нужны три
координатные оси, т.к.
 .
.
VI.
Амплитудный спектр
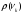 .
.
Опр.:
Амплитудным спектром
 комплексной
формы ряда Фурье называется модуль его
спектральной плотности.
комплексной
формы ряда Фурье называется модуль его
спектральной плотности.

Формула для нахождения амплитудного спектра.

Спектр четно-симметричен и может находиться только в верхней полуплоскости.
VII.
Фазовый спектр
 .
.
Опр.: Фазовым
спектром
 комплексной формы ряда Фурье называется
аргумент спектральной функции, взятый
с обратным знаком, т.е.
комплексной формы ряда Фурье называется
аргумент спектральной функции, взятый
с обратным знаком, т.е.

Вычисление фазового спектра.

Спектр
нечетно-симметричен и находится в полосе
от
 до
до
 .
.
Интеграл Фурье и преобразование Фурье.
Если функция
задана на всей числовой оси и не является
периодической, но удовлетворяет на
каждом конечном отрезке условиям
Дирихле, то ее можно представить
интегралом Фурье. Т.к. на отрезке
 функция удовлетворяет условиям Дирихле,
то можно, продолжив ее периодически с
периодом
функция удовлетворяет условиям Дирихле,
то можно, продолжив ее периодически с
периодом
 ,
представить рядом Фурье в комплексной
форме.
,
представить рядом Фурье в комплексной
форме.



Введем вспомогательное обозначение



С учетом введенного обозначения имеем:



Получили
представление для функции
 через интеграл на отрезке
через интеграл на отрезке
 .
Перейдем к пределу при
.
Перейдем к пределу при
 в последнем соотношении.
в последнем соотношении.
 (1)
(1)
- представление непериодической функции, заданной на всей числовой оси интегралом Фурье.
(1) – интегральная формула Фурье. Интеграл, стоящий в правой части (1) называется интегралом Фурье.
Достаточные условия представления функции интегралом Фурье.
Теорема:
Если функция
 удовлетворяет
трем условиям:
удовлетворяет
трем условиям:
1)
 задана на всей числовой оси
задана на всей числовой оси
2) на любом конечном отрезке числовой оси функция удовлетворяет условиям теоремы Дирихле.
3)
 абсолютно-интегрируема на всей числовой
оси, т.е.
абсолютно-интегрируема на всей числовой
оси, т.е.

тогда
функция представима интегралом Фурье
и при этом интеграл Фурье равен значению
 в каждой ее точке непрерывности, а в
точке разрыва I-го рода
интеграл Фурье равен
в каждой ее точке непрерывности, а в
точке разрыва I-го рода
интеграл Фурье равен

Вещественная форма интеграла Фурье.
Преобразуем
(1) с учетом формулы




Воспользуемся свойством интеграла по симметричному промежутку от четной и нечетной функции.
 -
четная
-
четная

 -
нечетная
-
нечетная


 (2)
(2)
- вещественная форма интеграла Фурье.
Прямое и обратное преобразования Фурье в комплексной форме.
Запишем соотношение (1) в виде

Введем вспомогательное обозначение
 (3)
(3)
Тогда
 (4)
(4)
Опр.: Соотношения (3) и (4) называются парой преобразований Фурье в комплексной форме, причем соотношение (3) называется прямым преобразованием Фурье в комплексной форме, а соотношение (4) называется обратным преобразованием Фурье в комплексной форме.
Замечание: На практике прямое преобразование(3) вычисляется (с помощью методов интегрирования), а соотношение (4) просто записывается.
Интеграл Фурье в виде, аналогичном ряду Фурье.
Преобразуем (2) с помощью формулы тригонометрии:



 (5) где
(5) где
 (6)
(6)
Соотношения (5) и (6) называют интегралом Фурье в вещественной форме, записанным в виде, аналогичном ряду Фурье, причем соотношение (6) называется прямым преобразованием Фурье в вещественной форме, а соотношение (5) – обратным преобразованием Фурье в вещественной форме.
Пара cos-преобразований Фурье для четной функции.
Пусть
 представлена интегралом Фурье и является
четной, тогда соотношения (5) и (6)
преобразуются к виду:
представлена интегралом Фурье и является
четной, тогда соотношения (5) и (6)
преобразуются к виду:




 (7)
(7)
 (8)
(8)
Соотношения (7) и (8) называют парой cos-преобразований Фурье, причем соотношение (8) называют прямым cos-преобразованием Фурье, а соотношение (7) – обратным cos-преобразованием Фурье.
Пара синус-преобразований Фурье для нечетной функции.
Поступая аналогично тому, как поступили в косинус-преобразовании Фурье, для нечетной функции имеем: соотношение (6) принимает вид:


Тогда,
 (9)
(9)
 (10)
(10)
Соотношения (9) и (10) называются парой синус-преобразований Фурье.
(9) – обратное, (10) – прямое.
Замечание:
Если функция
 задана
на промежутке
задана
на промежутке
 ,
то, продолжив ее соответственно четным
или нечетным образом, можно представить
эту функцию либо парой cos-,
либо парой sin-преобразований
Фурье.
,
то, продолжив ее соответственно четным
или нечетным образом, можно представить
эту функцию либо парой cos-,
либо парой sin-преобразований
Фурье.
Спектральные характеристики интеграла Фурье.
Выделяют 3 основные спектральные характеристики интеграла Фурье: спектральная плотность, амплитудный спектр, фазовый спектр.
Опр.№1:
Спектральной плотностью интеграла
Фурье называется функция
 .
.
Опр.№2: Амплитудным спектром интеграла Фурье называют модуль спектральной плотности

Опр.№3: Фазовым спектром интеграла Фурье называют аргумент спектральной плотности, взятый с противоположным знаком
 .
.

Найти прямое и обратное преобразование Фурье в комплексной форме.
 - прямое преобразование Фурье в комплексной
форме.
- прямое преобразование Фурье в комплексной
форме.
 - обратное преобразование Фурье в
комплексной форме.
- обратное преобразование Фурье в
комплексной форме.
Прямое преобразование находится, обратное просто записывается.





 - прямое преобразование Фурье в комплексной
форме.
- прямое преобразование Фурье в комплексной
форме.
 - обратное преобразование Фурье в
комплексной форме.
- обратное преобразование Фурье в
комплексной форме.
Спектральные характеристики преобразования Фурье.
1) Спектральная
плотность
 ,
,


2) Амплитудный спектр

3) Фазовый спектр

Найти прямое и обратное преобразование Фурье в комплексной форме.


 и т.д.
и т.д.
Найти пара косинус и пара синус преобразований Фурье.

1) Пара косинус преобразований Фурье
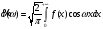 - прямое косинус-преобразование Фурье.
- прямое косинус-преобразование Фурье.
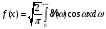 - обратное косинус-преобразование Фурье.
- обратное косинус-преобразование Фурье.
Прямое косинус-преобразование находится, обратное записывается.


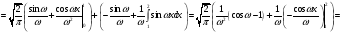
 - прямое косинус-преобразование Фурье.
- прямое косинус-преобразование Фурье.
 - обратное косинус-преобразование Фурье.
- обратное косинус-преобразование Фурье.
 - прямое синус-преобразование Фурье.
- прямое синус-преобразование Фурье.
 - обратное синус-преобразование Фурье.
- обратное синус-преобразование Фурье.

ТФКП.
Теория функций комплексного переменного.
Опр.:
Последовательностью комплексных чисел
 называется упорядоченный ряд
называется упорядоченный ряд
 комплексных чисел, когда каждому номеру
поставлено в соответствие свое комплексное
число.
комплексных чисел, когда каждому номеру
поставлено в соответствие свое комплексное
число.
Понятие окрестности точки.
Опр.:
Окрестностью точки
 называется множество точек комплексной
плоскости, удовлетворяющих условию
называется множество точек комплексной
плоскости, удовлетворяющих условию
 .
.
Геометрический
смысл окрестности точки
 .
.


Замечание:
Очевидно, что в комплексной плоскости
 представляет собой окрестность с центром
в точке
представляет собой окрестность с центром
в точке
 и радиуса
и радиуса
 .
.
Пример:
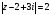
 .
.
Понятие предела последовательности комплексных чисел.
Опр.: Число
 называется
пределом последовательности комплексных
чисел
называется
пределом последовательности комплексных
чисел
 и обозначается
и обозначается
 ,
если
,
если




Т-ма: Для
того, чтобы
 ,
,
 сходилась к числу
сходилась к числу
 необходимо и достаточно, чтобы две
последовательности действительных
чисел
необходимо и достаточно, чтобы две
последовательности действительных
чисел
 ,
,
 сходились соответственно
сходились соответственно
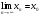 ,
,
 .
.
Вывод: Все теоремы, доказанные для последовательности действительных чисел, сохраняются и для последовательности комплексных чисел. В частности строгое неравенство переходит в нестрогое, нестрогое остается без изменения и т.д.
Понятие бесконечно удаленной точки.
Говорят,
что
 сходится к бесконечно удаленной точке
и пишут
сходится к бесконечно удаленной точке
и пишут
 ,
если
,
если



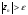 .
.
Понятие расширенной комплексной плоскости.
Опр.:
Комплексная плоскость
 с добавленным к ней несобственным
элементом
с добавленным к ней несобственным
элементом
 ,
называется расширенной комплексной
плоскостью и обозначается
,
называется расширенной комплексной
плоскостью и обозначается
 .
.
Геометрическая
иллюстрация
 (сфера
Римана, стереографическая проекция).
(сфера
Римана, стереографическая проекция).
Между
множеством точек сферы и комплексной
плоскости можно установить
взаимно-однозначное соответствие за
исключением одной точки
 ,
которую называют полюсом и ей отвечает
бесконечно удаленная точка.
,
которую называют полюсом и ей отвечает
бесконечно удаленная точка.
Понятие комплексной функции действительного переменного.
Опр.: Функция
 называется
комплексной функцией действительного
переменного и определяет в комплексной
плоскости некоторую ориентированную
кривую.
называется
комплексной функцией действительного
переменного и определяет в комплексной
плоскости некоторую ориентированную
кривую.
Опр.: Производной комплексной функции действительного переменного называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к 0

Формула для нахождения производной от комплексной функции действительного переменного.

Понятие гладкой кривой.
Опр.: Кривая
 называется гладкой, если функция
называется гладкой, если функция
 ,
при помощи которой кривая задана,
удовлетворяет двум условиям:
,
при помощи которой кривая задана,
удовлетворяет двум условиям:
1)
 непрерывно дифференцируема для любого
непрерывно дифференцируема для любого
 (т.е.
(т.е.
 и
и
 - непрерывны для любого
- непрерывны для любого
 ).
).
2)

 (т.е.
(т.е.

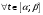 ).
).
Опр.: Кривая называется кусочно-гладкой, если ее можно разбить на конечное число гладких кривых.
Понятие области на комплексной плоскости.
Опр.:
Множество точек комплексной плоскости
 называются
областью, если оно удовлетворяет двум
условиям:
называются
областью, если оно удовлетворяет двум
условиям:
1)
 - открытое множество, т.е. содержит каждую
свою точку с некоторой окрестностью.
- открытое множество, т.е. содержит каждую
свою точку с некоторой окрестностью.
2)
 - связное множество, т.е. любые две точки,
лежащие в области, можно соединить
кривой, целиком лежащей в этой области.
- связное множество, т.е. любые две точки,
лежащие в области, можно соединить
кривой, целиком лежащей в этой области.
Понятие границы области.
Опр.: Точка
 является граничной точкой области
является граничной точкой области
 ,
если любая ее окрестность содержит как
точки, принадлежащие области, так и
точки, не принадлежащие области.
,
если любая ее окрестность содержит как
точки, принадлежащие области, так и
точки, не принадлежащие области.
Опр.:
Множество граничных точек области
называется ее границей и обозначается
 .
.
Замечание:
Граница области может быть задана с
помощью функции
 .
.
Понятие односвязной и многосвязной области.
Опр.: Область
 называется односвязной, если любую
замкнутую кривую, целиком лежащую в
области, можно непрерывно деформировать
в точку, оставаясь в этой области.
называется односвязной, если любую
замкнутую кривую, целиком лежащую в
области, можно непрерывно деформировать
в точку, оставаясь в этой области.
Опр.: Область называется n-связной, если ее граница распадается на n связных частей.
Понятие функции комплексного переменного.
Опр.: Функцией
комплексного переменного
 называется некоторое правило, по которому
каждому значению
называется некоторое правило, по которому
каждому значению
 ставится в соответствие одно (в случае
односвязной функции) или несколько (в
случае многосвязной функции) значений
ставится в соответствие одно (в случае
односвязной функции) или несколько (в
случае многосвязной функции) значений
 ,
при этом область
,
при этом область
 называется областью определения функции,
а область
называется областью определения функции,
а область
 -
областью значения функции.
-
областью значения функции.
Замечание:
Чтобы задать ФКП, достаточно задать две
функции
 и
и
 двух
действительных переменных.
двух
действительных переменных.
Пример:

Обратно, если заданы две функции двух действительных переменных, они определяют некоторую функцию комплексного переменного.



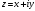







Предел ФКП в точке.
Опр.:
 называется пределом ФКП
называется пределом ФКП
 в точке
в точке
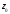 и
обозначается
и
обозначается
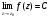 ,
если
,
если


 .
.
Предел ФКП в точке по Гейне.
Опр.: Число
 называется пределом ФКП
называется пределом ФКП
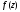 ,
если для любой сходящейся последовательности
комплексных чисел
,
если для любой сходящейся последовательности
комплексных чисел
 ,
соответствующая ей последовательность
комплексных чисел
,
соответствующая ей последовательность
комплексных чисел
 также сходится и ее предел
также сходится и ее предел
 .
.
Теорема о существовании предела ФКП.
Т-ма: Для
того, чтобы ФКП
 имела предел
имела предел
 ,
необходимо и достаточно, чтобы существовали
пределы функций двух переменных
,
необходимо и достаточно, чтобы существовали
пределы функций двух переменных
 и
и
 в точке
в точке
 ,
, ,
причем
,
причем
 и
и
 .
.
Замечание: Из этой теоремы ясно, что все теоремы о пределах функции нескольких переменных сохраняются для функции комплексного переменного.
Понятие непрерывности ФКП в точке.
Дадим три определения непрерывности ФКП в точке: на языке пределов, кванторов и приращений.
Опр.№1:
Функция комплексного переменного
 называется непрерывной в точке
называется непрерывной в точке
 ,
если предел функции в точке равен
значению функции в точке
,
если предел функции в точке равен
значению функции в точке
 .
.
Опр.№2:
Функция комплексного переменного называется непрерывной в точке
называется непрерывной в точке
 ,
если
,
если


 .
.
Опр.№3:
Функция комплексного переменного называется непрерывной в точке
называется непрерывной в точке
 ,
если бесконечно малому приращению
аргумента отвечает бесконечно малое
приращение функции, т.е.
,
если бесконечно малому приращению
аргумента отвечает бесконечно малое
приращение функции, т.е.
 ,
где
,
где

Опр.: Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Опр.:
Производной ФКП
 в точке
в точке
 называется предел отношения приращения
функции к приращению аргумента при
стремлении приращения аргумента к нулю
называется предел отношения приращения
функции к приращению аргумента при
стремлении приращения аргумента к нулю
 .
.
Опр.: Функция
комплексного переменного
 называется дифференцируемой в точке
называется дифференцируемой в точке
 ,
если в окрестности этой точки ее
приращение может быть представлено в
виде
,
если в окрестности этой точки ее
приращение может быть представлено в
виде
 ,
где
,
где
 - бесконечно-малая функция в точке
- бесконечно-малая функция в точке
 ,
,
 и
и
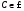 -
const.
-
const.
Опр.: Функция, дифференцируемая в каждой точке некоторого множества называется дифференцируемой на множестве функцией.
Теорема об эквивалентности понятий дифференцируемости и существования производной функции в точке.
Т-ма: Для
того, чтобы ФКП
 была дифференцируемой в точке, необходимо
и достаточно, чтобы в этой точке функция
имела производную.
была дифференцируемой в точке, необходимо
и достаточно, чтобы в этой точке функция
имела производную.
Необходимость:
Дано:
 - дифференцируема в точке
- дифференцируема в точке
 .
.
Доказать:
 .
.
Доказательство: Воспользуемся определением дифференцируемости



 (т.к.
(т.к.
 )
)

Достаточность:
Дано:
 .
.
Доказать:
 - дифференцируема в точке
- дифференцируема в точке
 ,
т.е.
,
т.е.
 .
.
Доказательство: Воспользуемся определением производной функции в точке


Введем вспомогательное обозначение
 (т.к.
(т.к.
 - Б.М.Ф.)
- Б.М.Ф.)
Во
вспомогательном обозначении проведем
операцию умножения на



 (т.к.
(т.к.
 - const)
- const)
Необходимое и достаточное условие дифференцируемости ФКП в точке (условие Даламбера-Эйлера, Коши-Римана).
Т-ма: Для
того, чтобы ФКП
 была дифференцируема в точке
была дифференцируема в точке
 необходимо и достаточно, чтобы выполнялись
два условия:
необходимо и достаточно, чтобы выполнялись
два условия:
1)
 - дифференцируемы в точке
- дифференцируемы в точке

2)


Необходимость:
Дано:
 - дифференцируема в точке
- дифференцируема в точке
 .
.
Доказать:
1)
 - дифференцируемы в точке
- дифференцируемы в точке

2)
 ,
,

Доказательство:
Поскольку дано, что
 ,
то предел, определяющий эту производную
существует, конечен и не зависит от
способа стремления
,
то предел, определяющий эту производную
существует, конечен и не зависит от
способа стремления
 к нулю. Вычислим эту производную двумя
способами и приравняем полученные
значения.
к нулю. Вычислим эту производную двумя
способами и приравняем полученные
значения.

а)
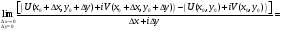


б)

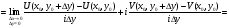

 - необходимость доказана
- необходимость доказана
Достаточность:
Дано: 1)
 - дифференцируемы в точке
- дифференцируемы в точке

2) К.-Р.:

Доказать:
 дифференцируема в точке
дифференцируема в точке
 .
.
Доказательство:
Поскольку функции
 дифференцируемы в точке
дифференцируемы в точке
 ,
воспользуемся определением
дифференцируемости функции двух
переменных, т.е. их приращения представимы
в виде
,
воспользуемся определением
дифференцируемости функции двух
переменных, т.е. их приращения представимы
в виде

 ,
,
где
 - Б.М.Ф. в точке
- Б.М.Ф. в точке
 .
.
Найдем приращение ФКП.


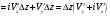


 дифференцируема в точке
дифференцируема в точке
 .
.
Замечание: при доказательстве теоремы были получены формулы для нахождения производной функции комплексного переменного, а именно:
 .
.
Понятие аналитической функции в точке.
Функция
комплексного переменного
 называется аналитической в точке
называется аналитической в точке
 ,
если она дифференцируема в этой точке
и некоторой ее окрестности.
,
если она дифференцируема в этой точке
и некоторой ее окрестности.
Функция, аналитическая в каждой точке некоторой области называется аналитической в этой области.
Понятие гармонической функции двух переменных.
Опр.: Функция
двух переменных
 называется
гармонической в некоторой области
называется
гармонической в некоторой области
 ,
если она дважды непрерывно дифференцируема
в этой области и удовлетворяет в ней
уравнению Лапласа:
,
если она дважды непрерывно дифференцируема
в этой области и удовлетворяет в ней
уравнению Лапласа:
 .
.
Понятие двух сопряженно гармонических функций.
Опр.: Две
функции двух переменных
 и
и
 называются сопряженно-гармоническими
функциями в области
называются сопряженно-гармоническими
функциями в области
 ,
если они являются гармоническими в этой
области
,
если они являются гармоническими в этой
области
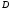
 и удовлетворяют в каждой точке области
условиям Коши-Римана:
и удовлетворяют в каждой точке области
условиям Коши-Римана:

Теорема о связи между аналитичностью и гармоничностью.
Т-ма: Для
того, чтобы ФКП
 была аналитической в области
была аналитической в области
 необходимо и достаточно, чтобы ее
вещественная и мнимая части
необходимо и достаточно, чтобы ее
вещественная и мнимая части
 и
и
 были сопряженно-гармоническими функциями.
были сопряженно-гармоническими функциями.
Необходимость:
Дано:
 - аналитическая в области
- аналитическая в области
 .
.
Доказать:
 - сопряженно-гармонические в области
- сопряженно-гармонические в области
 .
.
Доказательство:
т.к.
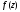 - аналитическая в области
- аналитическая в области
 ,
то она дифференцируема в каждой точке
этой области и в силу необходимости и
достаточности условия дифференцируемости
выполняются два условия:
,
то она дифференцируема в каждой точке
этой области и в силу необходимости и
достаточности условия дифференцируемости
выполняются два условия:
1)
 - дифференцируемы в области
- дифференцируемы в области

2) К.-Р.:

Найдем значение оператора Лапласа для этих функций.
 ,
,
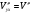 - теорема Шварца.
- теорема Шварца.

 - сопряженно-гармонические функции.
- сопряженно-гармонические функции.
Достаточность:
Дано:
 - сопряженно-гармонические
- сопряженно-гармонические
Доказать:
 - аналитическая в области
- аналитическая в области
 .
.
Доказательство:
Покажем, что
 .
.
Воспользуемся
тем, что функции
 и
и
 -
сопряженно-гармонические, тогда:
-
сопряженно-гармонические, тогда:
1)
 2)
2)
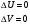
 функции
функции
 и
и
 дифференцируемы,
и для них выполняются условия Коши-Римана
в каждой точке, принадлежащей области
дифференцируемы,
и для них выполняются условия Коши-Римана
в каждой точке, принадлежащей области
 .
В силу необходимости и достаточности
условия дифференцируемости функции в
каждой точке области
.
В силу необходимости и достаточности
условия дифференцируемости функции в
каждой точке области

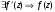 - аналитическая в области
- аналитическая в области
 .
.
Следствие из необходимого и достаточного условия дифференцируемости функции в точке.
Т-ма: Для
того, чтобы ФКП
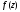 была дифференцируема в точке
была дифференцируема в точке
 необходимо и достаточно, чтобы ее
вещественная и мнимая части удовлетворяли
двум условиям:
необходимо и достаточно, чтобы ее
вещественная и мнимая части удовлетворяли
двум условиям:
1)
 - непрерывны в точке
- непрерывны в точке

2)

Восстановление аналитической функции по известной действительной или мнимой части.

Дано:
Доказательство:
Из теоремы
о связи между аналитичностью и
гармоничностью ясно, что данная задача
будет иметь решение, если
 .
Кроме того, искомая функция
.
Кроме того, искомая функция
 должна
быть сопряженно-гармонической к
должна
быть сопряженно-гармонической к
 ,
т.е.
,
т.е.

Обозначим
известные функции через
 .
Имеем систему для определения функции
.
Имеем систему для определения функции
 :
:


Проинтегрируем
 по
по
 и подставим найденную
и подставим найденную
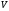 в
в
 .
.




Выражение,
стоящее в правой части соотношения для
 не зависит от переменной
не зависит от переменной
 .
Можно доказать, если производная по
.
Можно доказать, если производная по
 будет равна нулю.
будет равна нулю.
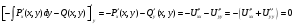
Т.к. полученное
выражение для
 не содержит переменной
не содержит переменной
 ,
можно найти
,
можно найти
 ,
вычислив интеграл по переменной
,
вычислив интеграл по переменной
 .
.
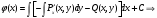 удалось
найти функцию
удалось
найти функцию
 :
:
 нашли
нашли
 .
.
