Достаточный признак разложимости функции в ряд Тейлора.

Теорема: Для того, чтобы функция была разложена в ряд Тейлора достаточно, чтобы функция в некотором интервале имела производные всех порядков и они были ограничены.

Доказательство:

Дано:

Доказать: 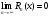, где - остаточный член формулы Тейлора.

Доказательство: Рассмотрим представление остаточного члена формулы Тейлора в форме Лагранжа

окрестности

Оценим остаточный член по абсолютной величине

Перейдем к пределу при :

Для вычисления введем в рассмотрение вспомогательный ряд.

Для каждого фиксированного 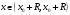имеем, вообще говоря, знакопеременный числовой ряд. Исследуем на абсолютную сходимость, т.е. рассмотрим ряд . Применим признак Даламбера:

Вывод: Вспомогательный ряд сходится абсолютно для . В силу необходимого признака сходимости числового ряда

, т.е. (1)

Для остаточного члена формулы Тейлора имеем:

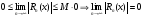
Алгоритм разложения функции в ряд Тейлора.

Шаг 1. Найти 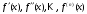и вычислить

Шаг 2. Записать ряд Тейлора для и найти область сходимости этого степенного ряда. Для этого найти радиус сходимости

, интервал сходимости и исследовать поведение ряда в концевых точках , .

Шаг 3. Выбрать из области сходимости множество таких точек , в которых остаточный член формулы Тейлора стремится к нулю, т.е.

Шаг 4. Выписать разложение формул в ряд Тейлора.

Опр.: Рядом Маклорена для функции называется ряд Тейлора, в котором точка .

Разложения основных элементарных функций в ряд Маклорена.

I.

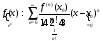
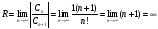
Областью сходимости построенного степенного ряда является вся числовая ось, т.е. . Рассмотрим остаточный член формулы Тейлора в форме Лагранжа.

Ответ:

II.

Область определения: ,

Формула для ряда Маклорена имеет вид:

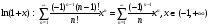
Сделаем замену индекса суммирования:

Ряд Маклорена для исследуемой функции принял вид:

Найдем радиус сходимости:

Интервал сходимости , т.к. точка в области определения функции не входит, то исследуем на сходимость степенной ряд в точке .

знакочередующийся ряд

I Абсолютная сходимость

расходящийся

II. Условная сходимость. Лейбниц:

- точка условной сходимости.

Область сходимости:

Выберем из области сходимости Х в каждой точке которой остаточный член формулы Тейлора стремится к нулю. Воспользуемся представлением в форме Коши.

Оценим остаточный член формулы Тейлора по абсолютной величине

Разобьем интервал :

1) Если ,

Перейдем к пределу в последнем соотношении при .

2) ,

Вывод: функция в области разложена в ряд Маклорена и это разложение имеет вид

Если в этом разложении заменить на -

Область сходимости построенного степенного ряда может изменяться только в концевых точках, т.е. при данный степенной ряд точно сходится, т.е. функция разложена в ряд Маклорена.

получили табличное разложение

Воспользуемся теоремой о дифференцируемости степенного ряда, в области сходимости равномерно сходящийся степенной ряд можно почленно дифференцировать.

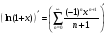
Подставим вместо

Проинтегрируем:

Приложения степенных рядов.

I. Вычисление пределов с помощью табличных разложений в ряд Маклорена.

Чтобы вычислить предел функции нужно:

1) Заменить табличными разложениями все элементарные функции, входящие в предел

2)Привести подобные, которые сокращаются

3) Вынести и сократить общий множитель

4) Перейти к пределу при

II. Решение линейных дифференциальных уравнений высшего порядка с непрерывными коэффициентами.

Пусть дано: (1)

где - непрерывные функции. Заданы начальные условия

Теорема: Если коэффициенты и функция - уравнения (1) разложены в окрестности точки в ряд Тейлора

то решение уравнения (1) также разложено в ряд Тейлора и имеет вид:

(без доказательства).

Пример: Найти первые 4 отличных от нуля члена разлож-я в степенной ряд решения дифференциального уравнения

Решение будем искать в виде:

Положим в исходящем уравнении :

.

продифференцируем:

Ответ: