
- •I. Первый признак сравнения.
- •II. Второй признак сравнения (признак сравнения в предельной форме).
- •Интегральный признак Коши-Маклорена.
- •Достаточный признак разложимости функции в ряд Тейлора.
- •Приложения степенных рядов.
- •Второй способ решения дифференциального уравнения.
- •III. Применение степенных рядов для приближенного вычисления значений функций.
- •Связь комплексной формы ряда Фурье с комплексным гармоническим колебанием.
- •Спектральные характеристики комплексной формы ряда Фурье.
- •Понятие интеграла от фкп.
- •Ряд Лорана.
Интегральный признак Коши-Маклорена.
Теорема:
Если для ряда с неотрицательными членами

существует
 ,
обладающая тремя свойствами:
,
обладающая тремя свойствами:


 -
монотонно невозрастающая или убывающая
функция.
-
монотонно невозрастающая или убывающая
функция.
Тогда ряд
и несобственный интеграл I-го
рода
 ведут себя одинаково, т.е. либо оба
сходятся, либо оба расходятся.
ведут себя одинаково, т.е. либо оба
сходятся, либо оба расходятся.
Доказательство:
Построим
геометрическую иллюстрацию графика
функции
 .
.


Проинтегрируем
неравенство по отрезку





Введем вспомогательное обозначение
 ,
тогда
,
тогда

Ряды
 и
и
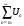 в силу неравенства ведут себя одинаково.
Исследуем на сходимость
в силу неравенства ведут себя одинаково.
Исследуем на сходимость
 .
Для этого рассмотрим его частичную
сумму.
.
Для этого рассмотрим его частичную
сумму.



Найдем предел последовательности частичных сумм

Ряд
 и несобственный интеграл
и несобственный интеграл
 ведут себя одинаково, следовательно,
также ведет себя
ведут себя одинаково, следовательно,
также ведет себя

 Ряд
Ряд
 ведет себя также, как и интеграл, т.к.
отличается на конечное число слагаемых.
ведет себя также, как и интеграл, т.к.
отличается на конечное число слагаемых.
Знакопеременные числовые ряды.
Опр.:
 называется знакопеременным числовым
рядом, если среди его членов имеется
бесконечное число как «+», так и «-».
называется знакопеременным числовым
рядом, если среди его членов имеется
бесконечное число как «+», так и «-».
Понятие абсолютной и условной сходимости знакопеременного ряда.
Опр.:
Знакопеременный числовой ряд
 называется абсолютно-сходящимся, если
сходится ряд, состоящий из модулей его
членов, т.е. сходится ряд
называется абсолютно-сходящимся, если
сходится ряд, состоящий из модулей его
членов, т.е. сходится ряд
 .
.
Опр.:
Знакопеременный числовой ряд
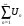 называется условно-сходящимся, если
сам ряд сходится, а ряд, состоящий из
модулей его членов расходится.
называется условно-сходящимся, если
сам ряд сходится, а ряд, состоящий из
модулей его членов расходится.
Теорема Эйлера.
Теорема: Если знакопеременный числовой ряд сходится абсолютно, то он сходится и в обычном смысле, т.е. существует и конечен предел последовательности его частичных сумм.
Доказательство:
Дано:
 - знакопеременный ряд,
- знакопеременный ряд,
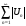 - сходится
- сходится
Доказать:
 - сходится.
- сходится.
Доказательство:
Т.к.
 - сходится, то в силу критерия Коши имеем:
- сходится, то в силу критерия Коши имеем:

Оценим:

Вывод:

Критерий
коши выполняется для
 ,
и он сходится.
,
и он сходится.
Знакочередующиеся числовые ряды.
Опр.:
Знакопеременный ряд
 называется знакочередующимся, если два
соседних члена этого ряда имеют
противоположные знаки, т.е.
называется знакочередующимся, если два
соседних члена этого ряда имеют
противоположные знаки, т.е.

Форма записи знакочередующегося ряда.
Знакочередующийся ряд можно записать:
 или
или

Признак Лейбница сходимости знакочередующегося ряда.
Теорема:
Если для знакочередующегося ряда
 выполняются два условия:
выполняются два условия:
1)

2)
 ,
то этот ряд сходится, и его сумма
неотрицательна и не превосходит первого
члена ряда, т.е.
,
то этот ряд сходится, и его сумма
неотрицательна и не превосходит первого
члена ряда, т.е.

Замечание: Признак Лейбница не дает ответа на вопрос о виде сходимости (абсолютная или условная).
Доказательство:
Рассмотрим
две последовательности частичных сумм
знакочередующегося ряда
 .
.
Покажем,
что обе последовательности сходятся,
причем к одному и тому же пределу
 .
Для этого покажем, что обе последовательности
монотонны.
.
Для этого покажем, что обе последовательности
монотонны.


(1)
 ,
,
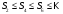 неубывающая (монотонная)
неубывающая (монотонная)
Рассмотрим вторую последовательность:



 (2)
(2)
 невозрастающая (монотонная)
невозрастающая (монотонная)
Докажем ограниченность числовой последовательности с четными индексами.

 ограничена снизу
ограничена снизу
 (3)
(3)

 ограничена сверху.
ограничена сверху.
Вывод:
 .
Доказали, что
.
Доказали, что
 монотонна и ограничена
монотонна и ограничена она обязательно сходится, т.е.
она обязательно сходится, т.е.
 .
.
Покажем,
что
 сходится к тому же пределу, что и
сходится к тому же пределу, что и
 .
Воспользуемся равенством
.
Воспользуемся равенством
 .
Перейдем в этом равенстве к пределу при
.
Перейдем в этом равенстве к пределу при
 .
.


Т.к.
 и
и
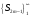 сходятся к одному и тому же пределу, то
сходятся к одному и тому же пределу, то
 ,
т.е. знакочередующийся ряд сходится.
,
т.е. знакочередующийся ряд сходится.
Геометрическая иллюстрация признака Лейбница.

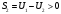





Функциональные ряды.
Опр.:
Функциональным рядом
 называется аналитическое выражение
вида
называется аналитическое выражение
вида
 ,
где
,
где
 - последовательность функций, определенных
в общей области
- последовательность функций, определенных
в общей области
 .
.
Опр.:
Функциональный ряд
 называется сходящимся в точке
называется сходящимся в точке
 ,
если числовой ряд
,
если числовой ряд
 сходится.
сходится.
Опр.: Множество точек, в которых функциональный ряд сходится, называется областью сходимости функционального ряда, а сама сходимость называется поточечной.
Понятие поточечной сходимости на языке кванторов.
Опр.:
Функциональный ряд
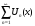 называется сходящимся поточечно в
области
называется сходящимся поточечно в
области
 ,
если
,
если
 (
( ),
где
),
где
 - n-ная частичная сумма
функционального ряда.
- n-ная частичная сумма
функционального ряда.
Понятие равномерной сходимости функционального ряда.
Опр.:
Функциональный ряд
 называется равномерно сходящимся в
области
называется равномерно сходящимся в
области
 ,
если
,
если
 .
В равномерной сходимости
.
В равномерной сходимости
 не зависит от
не зависит от
 .
.
Критеерий Вейерштрасса монотонной сходимости функционального ряда.
(Мажорантный признак функционального ряда).
Теорема:
Если для
 существует мажорантный сходящийся
чмсловой ряд
существует мажорантный сходящийся
чмсловой ряд
 ,
удовлетворяющий условию
,
удовлетворяющий условию
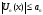
 ,
то функциональный ряд сходится, причем
абсолютно и равномерно в области
,
то функциональный ряд сходится, причем
абсолютно и равномерно в области
 .
.
Доказательство:
Воспользуемся
необходимым и достаточным условием
сходимости числового ряда
 (критерием
Коши). Т.к. ряд
(критерием
Коши). Т.к. ряд
 сходится, то для
сходится, то для
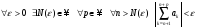 .
.
Рассмотрим
функциональный ряд
 и
воспользуемся условием
и
воспользуемся условием
 ,
тогда
,
тогда

Вывод:
 .
.
Функциональный
ряд сходится абсолютно
 и
и
 не зависит от
не зависит от

 сходимость
равномерная.
сходимость
равномерная.
Свойства равномерно сходящихся функциональных рядов.
(без доказательства)
 .
Если функциональный ряд
.
Если функциональный ряд
 сходится равномерно в области
сходится равномерно в области
 к сумме
к сумме
 и состоит из непрерывных функций, то
его сумма также является непрерывной
функцией.
и состоит из непрерывных функций, то
его сумма также является непрерывной
функцией.
 .
Свойство почленного дифференцирования.
.
Свойство почленного дифференцирования.
Если
функциональный ряд
 сходится равномерно в области
сходится равномерно в области
 и состоит из непрерывно дифференцируемых
функций, то сумма ряда также непрерывно
дифференцируемая функция и ряд можно
почленно дифференцировать:
и состоит из непрерывно дифференцируемых
функций, то сумма ряда также непрерывно
дифференцируемая функция и ряд можно
почленно дифференцировать:

 .
Свойство почленного интегрирования.
.
Свойство почленного интегрирования.
Если
функциональный ряд
 сходится равномерно в области
сходится равномерно в области
 и
и
 ,
то ряд можно почленно интегрировать:
,
то ряд можно почленно интегрировать:

Понятие степенного ряда.
Опр.:
Степенным рядом с центром в точке
 называется функциональный ряд
называется функциональный ряд
 ,
в котором члены ряда определяются
соотношением
,
в котором члены ряда определяются
соотношением
 ,
,
 ,
,
 - коэффициенты степенного ряда.
- коэффициенты степенного ряда.
Замечание:
Степенной ряд сходится в точке
 и его сумма в этой точке равна
и его сумма в этой точке равна
 .
Действительно:
.
Действительно:

Теорема Абеля (основная теорема степенных рядов).
.Теорема:
Если степенной ряд
 сходится
в точке
сходится
в точке
 ,
то он сходится, причем абсолютно и
равномерно для всех значений
,
то он сходится, причем абсолютно и
равномерно для всех значений
 ,
удовлетворяющих условию
,
удовлетворяющих условию
 ,
где
,
где
 .
.
Если
степенной ряд
 расходится
в точке
расходится
в точке
 ,
то он расходится для всякого значения
,
то он расходится для всякого значения
 ,
удовлетворяющего условию
,
удовлетворяющего условию ,
где
,
где
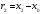 .
.
Доказательство:
Докажем первую часть теоремы.
Зафиксируем
значение
 ,
удовлетворяющее условию
,
удовлетворяющее условию
 .
Применим мажорантный признак (критерий
Вейерштрасса). Для этого оценим по
абсолютной величине общий член степенного
ряда.
.
Применим мажорантный признак (критерий
Вейерштрасса). Для этого оценим по
абсолютной величине общий член степенного
ряда.

При каждом
фиксированном
 ,
таком что
,
таком что
 имеем
имеем
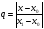 таково, что
таково, что
 ,
тогда
,
тогда

Воспользуемся
тем, что
 -
точка сходимости степенного ряда
-
точка сходимости степенного ряда
 сходящийся числовой ряд
сходящийся числовой ряд
 общий член ряда обязательно стремится
к нулю (необходимый признак сходимости
ряда), т.е.
общий член ряда обязательно стремится
к нулю (необходимый признак сходимости
ряда), т.е.
 .
.
Последовательность
 сходится. В силу необходимого признака
сходимости числовой последовательности,
она обязательно ограничена, т.е.
сходится. В силу необходимого признака
сходимости числовой последовательности,
она обязательно ограничена, т.е.

 .
Для степенного ряда имеем
.
Для степенного ряда имеем

 Б.У.Г.П.
Б.У.Г.П.

Вывод: В силу критерий Вейерштрасса сходится абсолютно и равномерно.
Докажем
вторую часть теоремы. Пусть
 -
точка расходимости степенного ряда.
-
точка расходимости степенного ряда.

Доказательство
проведем методом от противного. Пусть
в точке
 ряд сходится. В силу первой части теоремы
в точке
ряд сходится. В силу первой части теоремы
в точке
 степенной ряд должен сходиться, но это
точка расходимости
степенной ряд должен сходиться, но это
точка расходимости пришли к противоречию. Вторая часть
доказана.
пришли к противоречию. Вторая часть
доказана.
Понятие радиуса сходимости степенного ряда.
Опр.: Радиусом
сходимости степенного ряда
 называется положительное число
называется положительное число
 ,
удовлетворяющее двум условиям:
,
удовлетворяющее двум условиям:
1)
 - степенной ряд сходится
- степенной ряд сходится
2)
 - степенной ряд расходится
- степенной ряд расходится
при этом
 называется
интервалом сходимости степенного ряда,
а точка
называется
интервалом сходимости степенного ряда,
а точка
 концевыми точками интервала сходимости.
концевыми точками интервала сходимости.
Замечание:
О поведении степенного ряда в концевых
точках ничего сказать не можем. Это
требует отдельного исследования. Будем
считать, что
 ,
если степенной ряд сходится во всех
точках числовой оси, и
,
если степенной ряд сходится во всех
точках числовой оси, и
 если степенной ряд сходится в одной
точке
если степенной ряд сходится в одной
точке
 .
.
Отыскание радиуса сходимости степенного ряда.
Зафиксируем
 в степенном ряяде и исследуем его на
абсолютную сходимость.
в степенном ряяде и исследуем его на
абсолютную сходимость.
 К данному положительному числовому
ряду применим признак Даламбера.
К данному положительному числовому
ряду применим признак Даламбера.

 расходится
расходится
 сходится
сходится
Ряд сходится, если


Ряд расходится, если


Вывод:
Радиус сходимости равен
 .
.
Алгоритм исследования степенного ряда на сходимость.
Шаг 1. Найти радиус сходимости степенного ряда по одной из формул:
 ,
,

Шаг 2.
Вычислить интервал сходимости степенного
ряда
 и исследовать его поведение в концевых
точках
и исследовать его поведение в концевых
точках
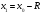 ,
,
 .
Для этого исследуем числовые ряды
.
Для этого исследуем числовые ряды
 и
и
 .
.
Шаг 3.
Выписать область сходимости степенного
ряда с учетом концевых точек. Она может
быть
 -
если в концевых точках получаются
сходящиеся числовые ряды,
-
если в концевых точках получаются
сходящиеся числовые ряды,
 ,
,
 - если в одной из концевых точек ряд
сходится, а в другой расходится,
- если в одной из концевых точек ряд
сходится, а в другой расходится,
 -
если в концевых точках получаются
расходящиеся ряды.
-
если в концевых точках получаются
расходящиеся ряды.
Замечание: Данный алгоритм действует для полного степенного ряда, в случае неполного степенного ряда для нахождения области сходимости применяют либо признак Даламбера, либо радикальный признак Коши.
Свойства степенных рядов.
Поскольку степенной ряд внутри интервала сходимости сходится абсолютно и равномерно (теорема Абеля), то все свойства равномерно сходящихся рядов сохраняются и для степенного ряда.
Разложение функции в степенной ряд.
Опр.: Если
степенной ряд
 сходится в некотором
сходится в некотором
 и его сумма равна
и его сумма равна
 ,
то говорят, что функция разложена в
степенной ряд и пишут
,
то говорят, что функция разложена в
степенной ряд и пишут
 .
.
Теорема единственности разложения функции в степенной ряд.
Теорема: Если удалось найти разложение функции в степенной ряд, то такое разложение единственно.
Доказательство:
Дано:

Доказать:
 ,
определяется единственным образом.
,
определяется единственным образом.
Доказательство: Воспользуемся свойством дифференцируемости равномерно сходящегося функционального ряда.
 имеем
имеем
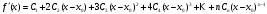


Из этих соотношений имеем

Вывод:
Коэффициенты степенного ряда определяются
по формулам
 ,
т.е. единственным образом.
,
т.е. единственным образом.
Необходимое и достаточное условия разложения функции в ряд Тейлора.
Опр.: Если
для некоторой функции
 построен
степенной ряд
построен
степенной ряд
 ,
в котором коэффициенты определяются
по формулам
,
в котором коэффициенты определяются
по формулам
 ,
то говорят, что функции поставлен в
соответствие ряд Тейлора.
,
то говорят, что функции поставлен в
соответствие ряд Тейлора.

Опр. Если
ряд Тейлора, построенный для функции
 сходится,
и его сумма в некотором интервале
сходимости
сходится,
и его сумма в некотором интервале
сходимости
 совпадает с
совпадает с
 ,
то говорят, что функция
,
то говорят, что функция
 разложена в ряд Тейлора, и вместо «
разложена в ряд Тейлора, и вместо « »
пишут «=».
»
пишут «=».
Замечание:
Ряд Тейлора может расходиться всюду за
исключением точки
 ,
или сходится в некотором интервале
,
или сходится в некотором интервале
 к некоторой функции
к некоторой функции
 .
В этом случае функция
.
В этом случае функция
 не разложена в ряд Тейлора и знак «
не разложена в ряд Тейлора и знак « »
нельзя заменить на «=».
»
нельзя заменить на «=».
Теорема:
Для того, чтобы функция
 была разложена в ряд Тейлора необходимо
и достаточно, чтобы остаточный член
формулы Тейлора стремился к нулю.
была разложена в ряд Тейлора необходимо
и достаточно, чтобы остаточный член
формулы Тейлора стремился к нулю.
Доказательство:
 Необходимость:
Необходимость:
Дано:
 разложена в ряд Тейлора
разложена в ряд Тейлора
 - сходится для
- сходится для

Доказать:

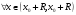 ,
где
,
где
 - остаточный член формулы Тейлора.
- остаточный член формулы Тейлора.
 Доказательство:
Выпишем
Доказательство:
Выпишем
 частичную сумму ряда Тейлора.
частичную сумму ряда Тейлора.

т.к. ряд
Тейлора сходится к функции
 ,
то
,
то
 .
.
Запишем
формулу Тейлора через
 :
:

Перейдем
к пределу при
 :
:


 - необходимость доказана.
- необходимость доказана.
 Достаточность:
Достаточность:
Дано:


Доказать:
 (
( разложена в ряд Тейлора)
разложена в ряд Тейлора)
Доказательство: Выпишем формулу Тейлора через частичную сумму:

Перейдем
к пределу при
 :
:

 .
.
