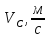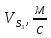1. Структурный анализ главного механизма
1.1.
Кинематическая схема главногомеханизма
По формуле Чебышева определим число степеней подвижности:
,
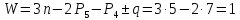где n=5
– число подвижных звеньев,
(
О(0,1);D(0,3);
(0,5);
А(1,2); В(2,3); С(4,5);B’(3,4)
) – число кинематических пар 5-го класса,
- число кинематических пар 4-го класса.
1.2. Построение структурной схемы механизма
Выделим
структурные группы (группы Ассура):
(0,1)
(2,3)
(4,5)
Формула
строения механизма:
(0,1) (2,3
(4,5)
2. Кинематическое исследование главного механизма
2.1. Определение масштаба длин
Для построения планов положения механизма определяем масштаб длин по формуле
µℓ
=
,
где
ℓОА
= 0,044 м – истинная длина кривошипа (звено
1);
= 44 мм – отрезок, изображающий на
кинематической схеме длину кривошипа
(задан произвольно).
Длины
звеньев на чертеже: 
2.2. Построение кинематической схемы главного механизма
В
масштабе µℓ
= 0,001
строим кинематическую схему главного
механизма в двенадцати положениях с
общей точкой О, включая положения, где
ползун 5 занимает верхнее и нижнее
положение (см. лист 1), разделив р
= 180
на 4, а х
= 180
на 3.
2.3 Построение планов скоростей и ускорений
Запишем векторные уравнения для построения планов скоростей и ускорений структурной группы 1-2, 2-4.
Векторные
уравнения скоростей: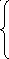
;
(2.1)
;
где
,
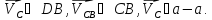
Векторные
уравнения ускорений: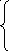 
(2.2)
Где
А=
ω12
•
ℓОА
= 6,3852
• 0,044 = 1,794
, направлен по звену 1 от А к О,
вектор
направлен по АВ от И к А; вектор
и
по модулю неизвестен.
2.4. Масштабы планов скорости и ускорения
Вычислим
масштабы планов скорости и ускорения
для построения планов скоростей и
ускорений:
-
масштаб плана скорости;
-
масштаб плана ускорения.
Предполагаем,
что
2.5. Графическое решение системы векторных уравнений
Решая графически системы векторных уравнений (2.1) и (2.2), строим планы скоростей и ускорений для всех положений механизма.
Рассмотрим например, положение 2.
На
плане скоростей: отрезок
Из построенного плана скоростей :
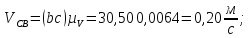
Данные
для всех положений
заносим в табл. 1.
Таблица 1.
|
№ Полож. |
(ab) |
|
|
(bc) |
|
(pc) |
|
|
|
|
|
1 |
48,84 |
0,31 |
0,05 |
8,42 |
0,05 |
8,64 |
0,055 |
0,36 |
0,05 |
0,096 |
|
2 |
44,45 |
0,28 |
0,19 |
30,50 |
0,19 |
26,38 |
0,17 |
0,44 |
0,21 |
0,34 |
|
3 |
12,12 |
0,08 |
0,27 |
43,02 |
0,27 |
23,65 |
0,15 |
0,57 |
0,288 |
0,37 |
|
4 |
28,33 |
0,18 |
0,23 |
36,3 |
0,23 |
6,47 |
0,04 |
0,47 |
0,23 |
0,24 |
|
5 |
44 |
0,28 |
0 |
0 |
0 |
0 |
0 |
0,37 |
0 |
0 |
|
6 |
35,16 |
0,225 |
0,24 |
37,81 |
0,24 |
6,86 |
0,44 |
0,5 |
0,25 |
0,26 |
|
7 |
18,14 |
0,12 |
0,18 |
29,08 |
0,18 |
27,67 |
0,18 |
0,5 |
0,2 |
0,34 |
На
плане ускорений:
;
Отрезок
где (ab)=44,45 мм из плана скоростей; (АВ)=171 мм из плана положения механизма.
Из
построенного плана ускорений:
Значения
отрезков
,
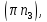а также модули скоростей и ускорений
для всех положений механизма занесем
в табл.2.