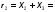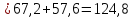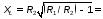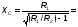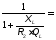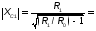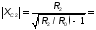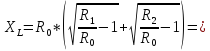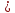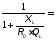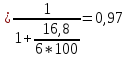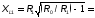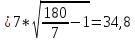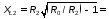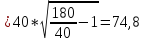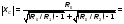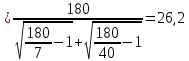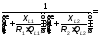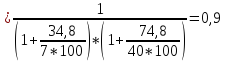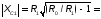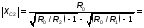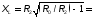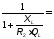6.3.Расчет согласующих цепей.
1.При расчете согласующей цепи выходного каскада необходимо определить коэффициент фильтрации, исходя из заданной выходной мощности в антенне РА и мощности второй гармоники Р2= 25 мВт.
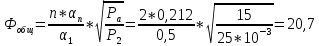
где n = 2 – номер гармоники
α1, αn – коэффициенты разложения последовательности косинусоидальных импульсов выходного тока.
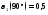 ;
;

Если коэффициент фильтрации задан в децибелах, то его надо пересчитать.
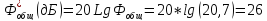
2.Полученный коэффициент фильтрации необходимо распределить между фильтром согласующей цепи выходного каскада Ф и антенным контуром ФА.
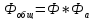
Для этого определим параметры антенного контура.
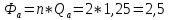
Q – добротность антенного контура.
Определим добротность антенного контура, имеющего сопротивление.
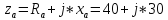
где RA– активное сопротивление антенны.
ХА – реактивное сопротивление антенны.
При
 :
:
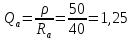
При
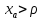 :
:
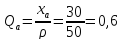
Волновое сопротивление ρ выбираем равным:
50 [Ом] или 75 [Ом], если антенны подключаются к выходному каскаду с помощью коаксиального кабеля,
или (200…400) [Ом] при подключении антенны с помощью двухпроводной линии.
3. Определим коэффициент фильтрации согласующей цепи выходного каскада.
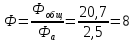
4. Исходя из требуемого коэффициента Ф, рассчитаем параметры согласующей цепи. Рассмотрим два варианта согласующей цепи. (RЭКВ =9 Ом)
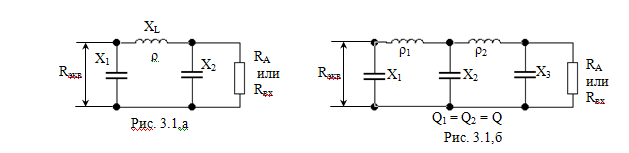
Исходным для расчета является выбор добротности колебательных контуров.
4.1. Для одиночного П-контура:
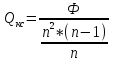 , при n=2
, при n=2
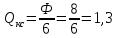
4.2.для сдвоенного П-контура:
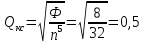
Далее задаемся
добротностью, величиной более рассчитанного
по формулам в п.4.4.1 или 4.4.2., но менее пяти
: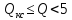
Если значения по
формулам в п.4.4.1 или 4.4.2. меньше единицы,
то задаются добротностью:
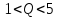
В дальнейших формулах подставляем величину добротности Q, которой задались для одиночного П-контура Q = 2, для сдвоенного – Q = 1,5.
При
расчетах промежуточных каскадов обычно
ограничиваются однозвенными фильтрами
(рис.3.1,а) или схемами (табл.3.1 ), т.к. не
целесообразно применять сложные фильтры,
поскольку последующие каскады работают
в режиме с отсечкой. Расчет фильтра
промежуточного каскада начинают с
п.4.4.3., далее по приведенной методике,
но вместо RА
подставляется входное сопротивление
следующего каскада
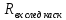 .
.
Таблица 3.1
|
Параметр контура |
Значения параметра для П-контура | |
|
одного |
двух | |
|
Полоса пропускаемых частот |
|
|
|
КПД системы контуров |
|
|
где Qx.x- добротность ненагруженного контура, Qx.x= 100
Прежде чем приступить к расчету параметров фильтра, необходимо убедиться также в том, что заданное сопротивление нагрузки (фидера или антенны) больше минимально допустимого.
. Для одного П-контура.
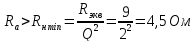
Для системы двух П-контуров.
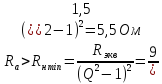
Сначала рассчитываются параметры схемы (рис.3.1,а) по формулам таблицы 3.2.
Таблица 3.2.
|
Этапы расчета |
Формулы для расчета схем | |
|
Рис. 3.1,а |
Рис. 3.1,б | |
|
1. |
| |
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
4.5.
Проверяем добротность:
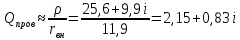
Если
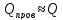 ,
то расчет фильтра верен.
,
то расчет фильтра верен.
Если в ф.5 (табл. 3.2) при определении реактивного сопротивления Х1 под корнем получается отрицательное число, то одиночный П-контур не реализуется. В этом случае необходимо задаться другой величиной добротности или рассчитать схему (рис.3.1,б). После расчета параметров двухзвенного фильтра (рис.3.1,б) также необходимо определить добротность:
4.6.
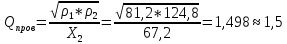
Полученная Qпров должна совпадать с выбранной добротностью Q (Qпров ≈Q, Q= 1.5 ).
Элементы фильтров определяются по формулам:
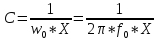 и
и
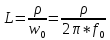
4.7.Рассчитаем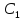 .
.
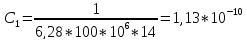 Ф
Ф

 .
.

Выбираем
из ряда Е24
=
0,3*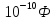
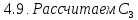 .
.
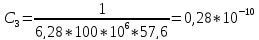 Ф
Ф
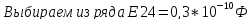
 .
.
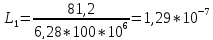 Гн
Гн
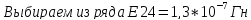
 .
.
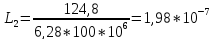 Гн
Гн
Выбираем из ряда
Е24=2*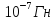
Причем надо иметь в виду, что в умеренном диапазоне частот (до 100 МГц) полученная индуктивность должна быть L> 50 нГн.
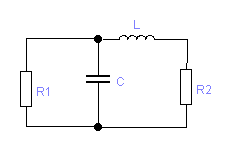
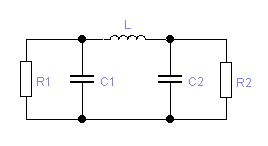
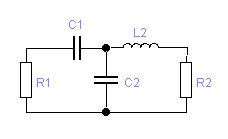
Если расчет рассмотренных вариантов согласующей цепи не получается, то можно рассмотреть другие виды фильтров: Г-, Т-, П-образных цепочек. В таблице 3.3 приведены схемы и расчетные формулы, в которых в качестве R1 используется эквивалентное сопротивление коллекторной нагрузки, в качестве R2 – активное сопротивление антенны или входное сопротивление следующего каскада. В цепях табл. 3.3 сопротивление R2 трансформируется в некоторое сопротивление R0 , а затем R0 - в R1. При этом чем меньше или больше R0 по отношению к R1, R2,тем лучшую фильтрацию будет обеспечивать П- и Т-цепочка, но тем ниже будет её КПД и уже полоса пропускания. Поэтому R0 выбирают в пределах 1,5…10 раз меньше или больше, чем R1 и R2.
Рассчитав емкости фильтров, необходимо номиналы конденсаторов выбирать по стандартному ряду, учитывая паразитные емкости транзистора (рис. 3.1,а).
4.12.Для одиночного:
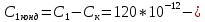

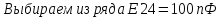
4.13.Для сдвоенного:
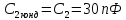
Выбираем из ряда Е24=30 пФ
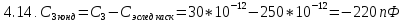
Для оконечного
каскада:
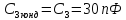
Выбираем из ряда Е24=30 пФ
Поскольку конденсатор с отрицательным номиналом не имеет смысла, рассчитываем фильтры другого типа, см. Табл. 3.3.
Аналогично подбираются конденсаторы для других вариантов схем.
Таблица 3.3
|
Схема |
Расчетные соотношения |
КПД
|
|
Общий случай | ||
|
Г-цепочка
|
при R1>R2 7 < 40, т.е. данный фильтр не подходит для рассчитываемого усилителя мощности
|
|
|
П-цепочка
|
R0<R1,R0<R2,R1 >R2 илиR1 <R2 7 < 40 фильтр подходит. Задаемся R0= 6 Ом
|
|
|
Т1-цепочка
|
R0>R1,R0>R2,R1 >R2 илиR1 <R2 7 < 40 фильтр подходит. Задаемся R0= 180 Ом
|
|
|
Т2-цепочка
|
R0>R1>R2 7 < 40 условие не выполняется
|
|
Элементы фильтров определяются по формулам:
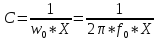 и
и
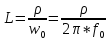
Рассчитаем П-цепочку.
 Ф
Ф
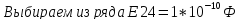
 Ф
Ф
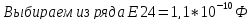
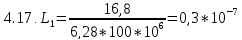 Гн
Гн
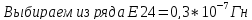
Причем надо иметь в виду, что в умеренном диапазоне частот (до 100 МГц) полученная индуктивность должна быть L> 50 нГн.

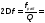

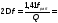

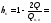
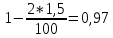
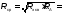
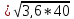 =12
Ом
=12
Ом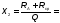
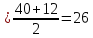

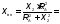

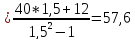
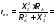
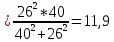
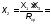


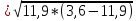 =9,9i
=9,9i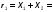
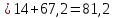
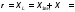
 i
i