Отсюда (11)

,

и, следовательно (10),

.

Аналогично вычисляются дальнейшие приближения. Результаты вычислений приведены в табл.1 (искомые значения функции выделены жирным шрифтом).

Таблица 1.

Интегрирование дифференциального уравнения (13) методом РунгеКутта

i	x	y
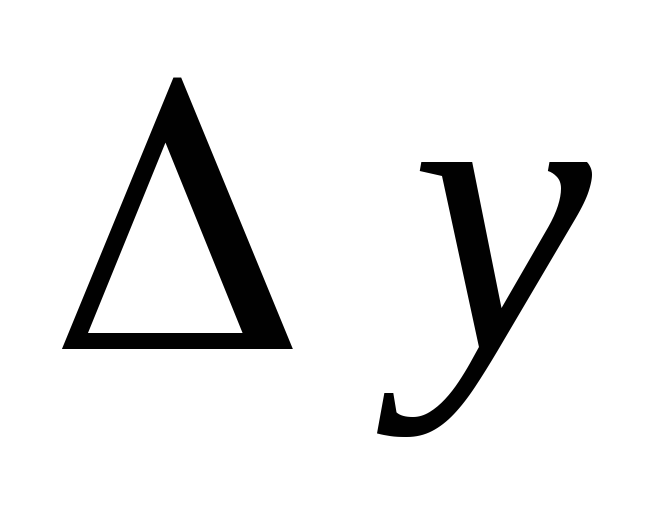
0	0	1	0,1	0,1000
	0,05	1,05	0,11	0,2200
	0,05	1,055	0,1105	0,2210
	0	1,1105	0,1210	0,1210
1	0,1	1,1103	0,1210	0,1210
	0,15	1,1708	0,1321	0,2642
	0,15	1,1763	0,1356	0,2652
	0,2	1,2429	0,1443	0,1445
2	0,2	1,2427	0,1443	0,1443
	0,25	1,3149	0,1565	0,3130
	0,25	1,3209	0,1571	0,3142
	0,3	1,3998	0,1700	0,1700
3	0,3	1,3996	0,1700	0,1700
	0,35	1,4846	0,1835	0,3670
	0,35	1,4904	0,1840	0,3680
	0,4	1,5836	0,1984	0,1984
4	0,4	1,5836	0,1984	0,1982
	0,45	1,6826	0,2133	0,4266
	0,45	1,6902	0,2140	0,4280
	0,5	1,7976	0,2298	0,2298
5	0,5	1,7974

Таким образом, . Уравнение (4.14) имеет точное решение, откуда

Метод Рунге  Кутта применим также для приближенного решения систем обыкновенных дифференциальных уравнений.

Пример.б. Методом Эйлера проинтегрировать уравнение (13), т.е.

на отрезке [0; 0.1] с шагом h= 0,05, при начальном условии.

Решение.

Определяем значение производной при = 0:

.

Теперь по формуле (4.8) вычисляем прих= 0,05

Вычисляем производную при =+h=0 + 0,05 = 0,05:

Искомое значение функции при =+h= 0,05 + 0,05 = 0,1 будет (см. (8))= 1,1050.

Дальнейшие вычисления продолжаем по формуле (7). Результаты представим в табличном виде (табл.2) (в графе 4 табл. 2 для сравнения приведены результаты точного решения уравнения (13), т.е. , для соответствующих значений аргументов, а в графе 5 приведены результаты имеющихся решений уравнения по методу Рунге-Кутта из табл.1;замечание: при выполнениизадания граф 4 и 5 составлятьне нужно).

Таблица 2.

Интегрирование дифференциального уравнения (13) методом Эйлера

i				(Р.- К.)
1	2	3	4	5
1	0,05	1,0500	1,0525	–
2	0,10	1,1050	1,1103	1,1103
3	0,15	1,1652	1,1738	–
4	0,20	1,2310	1,2428	1,2427
5	0,25	1,3026	1,3180	–
6	0,30	1,3802	1,3997	1,3996
7	0,35	1,4642	1,4881	–
8	0,40	1,5549	1,5836	1,5836
9	0,45	1,6527	1,6866	–
10	0,50	1,7578	1,7974	1,7974