Тема 5. Решение задач линейного программирования средствами табличного процессора ms Excel .

Для решения задач линейного программирования в MS Excel имеется надстройка Поиск решения. По умолчанию в Excel надстройка Поиск решения отключена. Чтобы активизировать ее в MS Excel 2007, щелкните значок Кнопка Microsoft Office , щелкните Параметры MS Excel, а затем выберите категорию Надстройки. В поле Управление выберите значение Надстройки MS Excel и нажмите кнопку Перейти (см. рис. 5.1).

В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК (см. рис. 5.2).

В Excel 2003 и ниже выберите команду Сервис→Надстройки, в появившемся диалоговом окне Надстройки установите флажок Поиск решения и щелкните на кнопке ОК. Если вслед за этим на экране появится диалоговое окно с предложением подтвердить ваши намерения, щелкните на кнопке Да. (Возможно, вам понадобится установочный компакт-диск MS Office).

рис. рис 5.1

рис. 5.2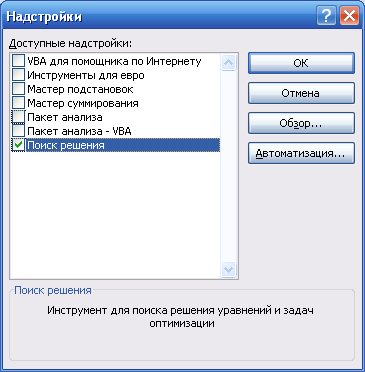

Рассмотрим использование данной надстройки для решения задачи линейного программирования из примера 6.

1. Для решения задачи с помощью функции Поиск решения необходимо внести исходные данные – это диапазон ячеек (A5:F10) на рис. 5.3.

2

рис. 5.3

. Затем определить ячейки для результата решения задачи-неизвестные величиныx_j, отражающие план производства изделий A, B, С и D. Ячейки для неизвестных величин заполнить нулями – это диапазон ячеек (B15:E15) на рис. 5.3.

рис. 5.3

3. В ячейке F15 для вычисления значения общей стоимости всей произведенной предприятием продукции - ввести формулу =СУММПРОИЗВ(В10:E10;В15:E15), которая находит сумму попарных произведений ячеек с ценами (В10:E10) на ячейки со значениями неизвестных величин (В15:E15).

4. Для задания ограничений по видам сырья в ячейку G7 скопировать формулу из ячейки F15. Она скопируется в виде СУММПРОИЗВ(C2:F2;C7:F7). Необходимо заменить диапазон (C2:F2) на диапазон параметров расхода сырья (В7:E7), а диапазон (C7:F7) на диапазон (В15:E15)- значения неизвестных величин .

Диапазон (В15:E15) преобразуется к абсолютному виду для удобства дальнейшего копирования формулы в ячейки с ограничениями. Для такого преобразования необходимо при наборе формулы после выделения нужного диапазона ячеек в таблице (В15:E15) нажать клавишу F4, чтобы получилась формула =СУММПРОИЗВ(B7:E7;$B$15:$E$15).

Для задания остальных ограничений скопировать вновь введенную формулу в ячейки G8 и G9. На рис. 5.3 ячейки содержащие формулы закрашены серым цветом.

5. После создания таблицы с исходными данными установить курсор в ячейку с формулой целевой функции (F15) и выбрав в меню Сервис функцию Поиск решения в Excel 2003 или Данные→Анализ→Поиск решения в Excel 2007. Затем заполнить поля в появившемся окне

в

рис. 5.3

полеУстановить целевую ячейку должен появиться адрес ячейки с формулой целевой функции (в данном случае $F$15);

• установить переключатель вида оптимизации в поле Равной: в положение максимальное (минимальное) значение, при необ­ходимости найти максимум или минимум целевой функции;

• в поле Изменяя ячейки указать диапазон ячеек со значениями неизвестных задачи, выделив его в таблице. В данном примере это ячейки $B$15:$E$15;

• в поле Ограничения задать вид и значения ограничений. Для этого установить курсор в поле ввода ограничений и нажать кнопку Добавить. После чего в появившемся окне Добавление ограничения ввести в поле Ссылка на ячейку адрес ячейки с формулой соответствующего ограничения (например, $G$7 для ресурса I –го вида). Затем ввести в поле Огра­ничение предельное значение соответствующего ресурса (оно находится в ячейке $F$7) и выбрать вид от­ношения (<, >, = и т.п.). (см. рис. 5.4).

рис. 5.4

После нажатия кнопки Добавить (или OK для ввода послед­него ограничения) данное ограничение попадает в список огра­ничений задачи.

С помощью кнопок Удалить и Изменить можно удалять вы­деленные в списке ограничения или вносить в них исправления.

После заполнения всех полей окна нажать кнопку Параметры в открывшемся окне Параметры поиска решения (рис 5.5) установить флажки Линейная модель для решения задачи линей­ного программирования и Неотрицательные значения, если такие ограничения накладываются на все переменные задачи.

В этом окне можно так же определить параметры процесса решения: предельное время поиска решения, максимальное ко­личество итераций, точность и т.п.

Флажок Показывать результа­ты итераций позволяет по шагам следить за поиском решения.

Флажок Автоматическое масштабирование включается в том случае, когда разброс значений параметров очень велик.

рис. 5.5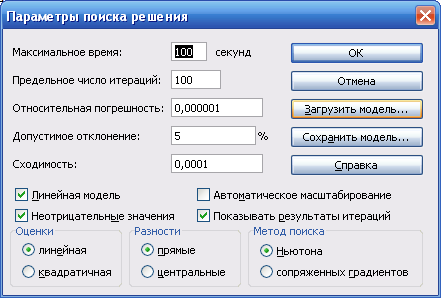

Параметры средства Поиск решения.

Таблица 5.1

Максимальное время	-служит для ограничения времени, отпущенного на поиск решения задачи. В этом поле можно ввести время в секундах, не превышающее 32 767 (примерно девять часов); значение 100, используемое по умолчанию, вполне приемлемо для решения большинства простых задач.
Предельное число итераций	-управляет временем решения задачи путем ограничения числа вычислительных циклов (итераций).
Относительная погрешность	- определяет точность вычислений. Чем меньше значение этого параметра, тем выше точность вычислений.
Допустимое отклонение	- предназначен для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. Чем больше значение допуска, тем меньше времени требуется на поиск решения.
Сходимость	- применяется только к нелинейным задачам. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается.
Линейная модель	- служит для ускорения поиска решения путем применения к задаче оптимизации линейной модели. Нелинейные модели предполагают использование нелинейных функций, фактора роста и экспоненциального сглаживания, что замедляет вычисления.
Неотрицательные значения	- позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых не было задано соответствующее ограничение в диалоговом окне Добавить ограничение.
Автоматическое масштабирование	- используется, когда числа в изменяемых ячейках и в целевой ячейке существенно различаются.
Показывать результаты итераций	- приостанавливает поиск решения для просмотра результатов отдельных итераций.
Загрузить модель	- после щелчка на этой кнопке отрывается одноименное диалоговое окно, в котором можно ввести ссылку на диапазон ячеек, содержащих модель оптимизации.
Сохранить модель	- служит для отображения на экране одноименного диалогового окна, в котором можно ввести ссылку на диапазон ячеек, предназначенный для хранения модели оптимизации.
Оценка линейная	- выберите этот переключатель для работы с линейной моделью.
Оценка квадратичная	- выберите этот переключатель для работы с нелинейной моделью.
Разности прямые	- используется в большинстве задач, где скорость изменения ограничений относительно невысока. Увеличивает скорость работы средства Поиск решения.
Разности центральные	- используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдано сообщение о том, что получить более точное решение не удается.
Метод поиска Ньютона	- требует больше памяти, но выполняет меньше итераций, чем в методе сопряженных градиентов.
Метод поиска сопряженных градиентов	- реализует метод сопряженных градиентов, для которого требуется меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно большая и необходимо экономить память или если итерации дают слишком малое отличие в последовательных приближениях.

Задав все параметры, нажать кнопку Выполнить для поиска решения задачи. Если решение найдено, то появляется окно, с соответствующим сообщением (рис. 5.6).

рис. 5.6

Результаты решения могут быть сохранены в файле задачи в виде сценарии или добавлены в виде отдельных листов Отчет по результатам, Отчет по устойчивости, Отчет по пределам. Для сохранения результатов в виде листов необходимо предварительно в поле Тип отчета выделить требуемые типы отчетов. В этом же окне можно отказаться от полученных решений и восстановить ис­ходные значения переменных.

Отчет по результатам приведен ниже на рис. 5.7. В данном отче­те в графах Результат выводятся значения целевой функции и оптимального плана, а также значения исходного опорного пла­на (графа Исходное значение). Кроме того, указывается, какие ограничения являются связанными, т.е. ограничения с дефи­цитным ресурсом (т.е его количество ограничивает план производства), а какие — нет (графа Статус), и приведены значения соответствующих дефицитов по всем ограничениям (графа Разница).

Отчеты по устойчивости и по пределам позволяют проанализировать модель на устойчивость. Устойчивость модели имеет важную роль на практике. Если значение оптимального решения резко изменяется при небольших отклонениях переменных, то такой моделью сложно пользоваться на практике, где изменения цен и запасов – явление обыденное. Возможности MS Excel анализировать модель на устойчивость в данном пособии не рассматриваются.

рис. 5.7