-
Определение ускорений точек механизма
Шарнирно – рычажный механизм (см. рис. 2а). Для определения ускорений воспользуемся уравнениями, подобными уравнениям, с помощью которых рассчитывались скорости.
Полное ускорение точки А состоит из двух составляющих:
=
+
где
- нормальное ускорение, направленное
по радиусу ОА к центру 0;
- касательное ускорение, направленное
перпендикулярно ОА и в сторону
углового ускорения.
Составляющие ускорения точки А равны
=
· lOA, м/с2;
=
· lOA м/с2.
Так как ω1 =
const, то аА =
.
Выбираем (определяем) масштаб ускорений
ка, м/с2мм и на плане (см.
рис. 2в) ускорений строим отрезок zА
(о'a'):
zА =
,
мм.
Ускорение точки В находим из уравнения, подобного уравнению (1):
+
=
+
+
,
Находим величины
и
:
=
,
=
.
Отрезки, изображающие
эти ускорения в масштабе ка,
будут равны
=
,
мм;
=
,
мм.
Из полюса плана
ускорений о' проводим
параллельно ВС и в сторону точки С,
а также
из конца вектора zA параллельно
АВ и в сторону точки А. Через концы
векторов
и
проводим направления
и
,
точка пересечения которых в' определяет
отрезки, пропорциональные этим
ускорениям, тогда
= ка ·
,
м/с2;
= ка ·
,
м/с2.
Соединив точки а' и в', получим полное относительное ускорение:
= ка ·
,
м/с2,
если относительное движение вращательное, то ускорение пропорционально расстояния до осей вращения:
=
,
=
,
м/с2
или
=
,
=
,
мм.
Отложив отрезок
= а'·s'2 на плане ускорения
по направлению а'в', найдем ускорение
центра масс шатуна s2:
= ка ·
,
м/с2.
Аналогично находим ускорение точек S3 и Е:
=
;
=
,
мм;
=
;
=
,
мм.
Для определения ускорения точки D составляем два уравнения подобных уравнениям (3)
=
+
+
,
=
+
+
.
Нормальные составляющие относительных ускорений равны
=
,
м/с2;
=
,
мм;
=
,
м/с2;
=
,
мм.
Из точки а' откладываем
на плане ускорений вектор
,
а из точки в' - вектор
.
Из концов этих векторов проводим
направления касательных составляющих
и
до пересечения (точка а').
Получим отрезки
и
,
по которым определим величины
касательных составляющих:
= ка ·
,
м/с2;
= ка ·
,
м/с2.
Соединив точку d' с точками о', a' и в', получим величины следующих полных ускорений:
аD = ка · zD, м/с2; аD/А = ка · zD/А, м/с2; аD/В = ка · zD/В, м/с2.
Ускорение точки F найдем из уравнения подобного уравнению (4):
+
.
Определим нормальную составляющую:
=
,
м/с2.
Из конца вектора о'e' откладываем отрезок на плане ускорений параллельно EF и в сторону Е:
=
,
мм.
Через конец вектора
и полюс о' проводим направления
ускорений
и
.
Точка пересечения f ' определяет
их величины:
= ка · zF, м/с2;
= ка ·
,
м/с2.
Соединив на плане ускорения точки е' и f ', получим полное ускорение:
= ка · zF/Е, м/с2.
Для нахождения точки S4 составим отношение
=
;
=
.
Отложив s4'e'
на направление e'f ', получим отрезок
о's4', пропорциональный
ускорению
:
= ка ·
,
м/с2.
Кулисный механизм. Случай 1 (см. рис. 3а) Составим уравнение, аналогичное уравнению (5).
.
Ускорение точки А
определяется так же, как и для
предыдущего механизма. Нормальная
составляющая
=
,
м/с2.
Величина Кориолисова ускорения ак определяется из выражения
ак = 2 ω3 · VA/3,
где ω3 - угловая скорость кулисы 3; · VA/3 - относительная скорость.
Для нахождение направления ак необходимо вектор относительной скорости VA/3 повернуть на 90º по направлению ω3 (см. рис. 3г).
Находим отрезок zA
(о'a'): zA =
,
мм
И откладываем отрезки
и
,
пропорциональные ускорениям
и
:
=
,
мм;
=
,
мм.
Отрезок
откладываем из полюса о' параллельно
CD и в сторону точки С, а отрезок
проводим через конец вектора zA
так, чтобы
и
представляли геометрическую разность.
Через конец вектора
проводим перпендикулярно CD ускорение
,
через конец
- ускорение
параллельно CD.
Соединив точку в'
пересечения
и
с полюсом о', найдем
= ка ·
,
м/с2;
= ка ·
,
м/с2;
= ка ·
,
м/с2.
Для кулисы 3 ускорение точек S3, В и D пропорциональны расстояниям до точки С:
=
;
=
,
откуда
=
,
мм;
=
,
мм
и откладываем на плане ускорений.
Кулисный механизм.
Случай 2 (см. рис. 4а) Величину
ускорения точки А находим аналогично
случаю 1 и откладываем на плане
ускорения (отрезок
,
рис. 4г).
Для определения ускорения точки составим два уравнения подобных (6) и (6):
=
+
+
=
+
+
(аС = 0).
Далее находим величины ускорений:
=
,
м/с2; ак = 2 ω2 · VB,
м/с2,
где ω2 - угловая скорость 2; скорость VB равна относительной скорости VB/С (см. с.10). Направление ускорения Кориолоса показано на рис. 4в. Определим отрезки, пропорциональные найденным ускорения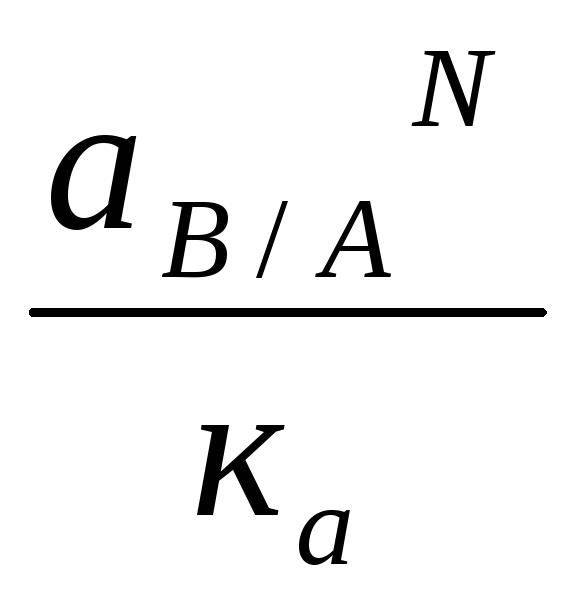м:
=
,
мм;
=
,
мм.
Вектор
прибавляем к вектору zA, а вектор
zK проводим из полюса о'. Из
концов этих векторов проводим
направления
и
,
точка пересечения в' которых
позволяет найти неизвестные ускорения
(предварительно соединив точки о'
и в', а' и в'):
= ка ·
,
м/с2;
= ка ·
,
м/с2;
= ка ·
,
м/с2;
= ка ·
,
м/с2.
Ускорения точек S2 и D определяем из пропорций
=
;
=
.
Находим отрезки
и
:
=
,
мм; 
=
,
мм.
и откладываем их на плане ускорений. Соединив полюс о' с точками s2' и d', получим
= ка ·
,
м/с2; 
= ка ·
,
м/с2.