
- •Исследование шарнирно – рычажного механизма
- •Порядок выполнения задания
- •Построение схемы механизма
- •Построение траектории центров масс
- •Определение скоростей точек механизма
- •Определение ускорений точек механизма
- •Определение угловых скоростей и угловых ускорений
- •Определение радиуса кривизны
- •Определение сил в кинематических парах механизма
Исследование шарнирно – рычажного механизма
Для выполнения данного раздела проекта необходимо ознакомиться с литературой [1-3]. Исходные данные для проектирования приведены в прил. 1, 2 и 3 настоящего руководства.
Порядок выполнения задания
1. Построить в тонких линиях схему механизма (рис. 1) в 12 положениях в заданном масштабе КL, м/мм. Для всех вариантов задания КL = 0,005 м/мм. Два заданных положения обвести (положения указаны в прил. 1).
2. Построить траекторию движения центров масс шатунов.
3. Для двух заданных положений определить скорости точек, указанных на механизме. Масштаб скорости КV м/с·мм выбирать при условии, что скорость VА точки А ведущего звена на плане скоростей пропорциональна отрезку оа = 70 мм.
4.
Для двух заданных положений найти
ускорения точки. Масштаб ускорения
определить по формуле
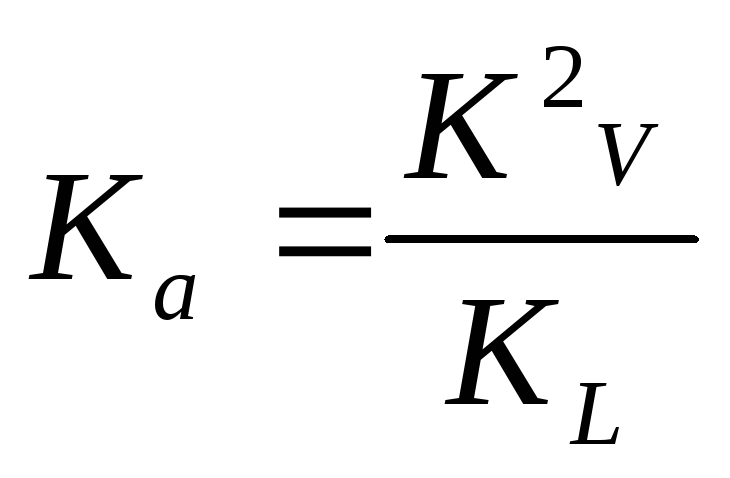 м/ смм, либо задается самим.
м/ смм, либо задается самим.
5. Рассчитать угловые скорости и угловые ускорения звеньев для заданных положений, показать их направления на схеме механизма.
6. Для одного из заданных положений найти радиусы кривизны траектории движения центров масс шатунов и показать их на схеме механизма.
7.
Для одного из заданных положений
определить силы, приложенные к звеньям,
найти момент сопротивления, приложенный
к ведущему звену. При этом величина
силы Р =
![]() ,
где R – равнодействующая звена, к
которому она приложена.
,
где R – равнодействующая звена, к
которому она приложена.
-
Построение схемы механизма
Длины звеньев механизма (рис. 1) lOA, lAB, lBC, lEF, lEC и расстояния Х1, У1 заданы в метрах. Положения центров масс S2, S3, S4 и точки D известны. Размеры звеньев механизма определяем в заданном масштабе КL в миллиметрах:
ОА
=
![]() ,
АВ =
,
АВ =
![]() ,
….., х1
=
,
….., х1
=
![]() ,
у1
=
,
у1
=
![]() .
.
Схему механизма строим методом засечек. После построения механизма в 12 положениях обводим два заданных положения (на рис. 1 обведены 5 и 10 положения).
-
Построение траектории центров масс
На всех 12 положениях наносим положения центров масс S2 и S4 и средним их плавной кривой, в результате чего получим траектории центров масс шатунов 2 и 4 (см. рис.1).
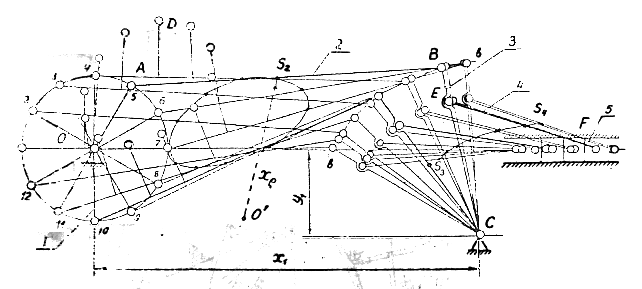
Рис. 1
-
Определение скоростей точек механизма
В курсовом проекте рассматриваются различные шарнирно-рычажные и кулисные механизмы. Рассмотрим их в отдельности.
Шарнирно-рычажный механизм (рис. 2а). Заданы размеры механизма, величина и направление угловой скорости ведущего звена (см. прил. 1). Угловая скорость постоянна. Скорость точки А определяем по формуле VA=ω1lOA, м/с. Из точки О (рис. 2б), которая называется полюсом плана скоростей, откладываем перпендикулярно ОА отрезок оа, соответствующий скорости точки А. Масштаб скорости будет равен
КV =
![]() ,
м/с·мм.
,
м/с·мм.
Затем определяем скорость точки В, которая является общей для звеньев 2 и 3. Используя теорему о сложении скоростей в переносном и относительном движениях, запишем векторное уравнение, связывающее скорости точек А и В:
![]() +
+![]() .
(1)
.
(1)
Здесь одной чертой подчеркивается скорость, известная по направлению (направление указано), и двумя чертами - скорость, известная по величине и направлению. Из точки О (абсолютная скорость всегда проходит через полюс) проводим направление скорости VB, а из точки а - направление VВ/А. Точка пересечения этих линий в определяет величины неизвестных скоростей:
VB = кV · ов, м/с; VB/А = кV · ав, м/с.
Учитывая, что при вращательном движении относительные и абсолютные скорости пропорциональны расстоянию до оси вращения, находим скорости центров масс шатуна 2, коромысла 3 и точки Е:
![]() ;
;
![]() ,
м/с (2)
,
м/с (2)
или
![]() =
=
![]() ;
аs2 = ab
;
аs2 = ab![]() ,
мм.
,
мм.
Отложив отрезок аs2
на плане скоростей по направлению
ав и соединив О и S2,
определим скорость
![]() :
:
![]() = к V ·as2, м/с.
= к V ·as2, м/с.
Аналогично рассчитаем скорости S3 и Е:
![]() =
=
![]() ;
os3 =
;
os3 =
![]() , мм
, мм
![]() =
=
![]() ;
oе =
;
oе =
![]() , мм.
, мм.
Найденные отрезки откладываем на плане скоростей.
Скорость точки D находим из уравнений, подобных уравнению (1):
![]() ,
,
![]() .
(3)
.
(3)
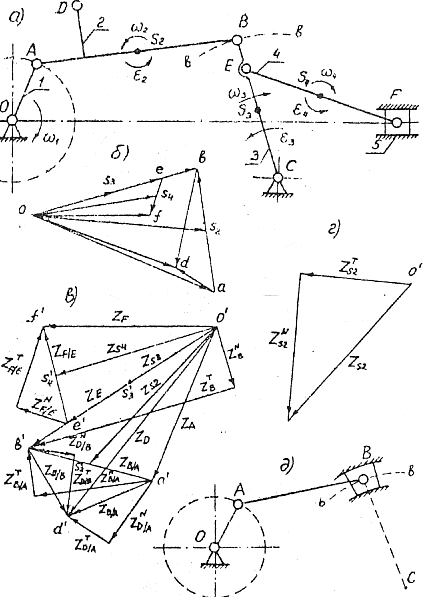
Рис. 2
Направление скорости
VD/A проводим через точку а
(см. рис. 2б), в направление VD/В
- через точку в. Точку их пересечения
d соединяем с полюсом скоростей о м
находим скорость точки D
![]() = к V ·ad, м/с. Для определения
скорости точки F составим уравнение
= к V ·ad, м/с. Для определения
скорости точки F составим уравнение
![]() (4)
(4)
Из полюса о
проводим горизонтальную линию, а из
точки е - прямую, перпендикулярную
EF, до пересечения с горизонтальной.
Получим точку f, тогда
![]() = к V ·af, м/с;
= к V ·af, м/с;
![]() = к V ·еf, м/с.
= к V ·еf, м/с.
Находим скорость точки S4:
![]() =
=
![]() ;
s4е =еf
;
s4е =еf
![]() .
.
Отложив отрезок s4е
на прямой еf,
соединяем полюс о с точкой s4,
тогда
![]() = к V ·оs4, м/с.
= к V ·оs4, м/с.
На рис. 2 д показан механизм с ползушкой, которая перемещается по дуге вв с радиусом в точке С. Определение скоростей в этом случае не отличается от вышеизложенного.
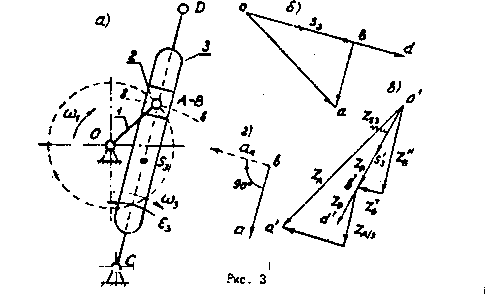
Кулисный механизм. Случай I. В механизме изображенном на рис. 3, точка А принадлежит кривошипу 1 и ползуну 2 и совершает движение по окружности радиусом ОА. Точка В принадлежит кулисе 3, которая совпадает с точкой А и перемещается в данный момент времени по траектории вв. Скорость точки А определяется так же, как в механизме с кривошипом и коромыслом (см. рис. 2а). Поворот кулисы 3 будем считать переносным движением, а движение ползуна 2 вдоль паза кулисы относительным. Тогда на основании той же теоремы о сложении переносного и относительного движений запишем
![]() .
(5)
.
(5)
Из полюса О плана
скоростей (рис. 3б) проводим отрезок
оа, пропорциональный скорости
точки А, затем направления скоростей
VB и VА/3 до пересечения в
точке в, которая определяет длины
отрезков последних. Отсюда VB=
кV · ов, м/с; VA/3=кV ·
ав, м/с. Так как точки В, S3
и D лежат на одной прямой и принадлежат
звену 3, их относительные скорости
пропорциональны расстояниям
![]() =
=
![]() ;
;
![]() =
=
![]() ,
,
откуда оs3 =
![]() ,
мм; оd =
,
мм; оd =
![]() ,
мм откладываем на плане скоростей
9см. рис. 3б).
,
мм откладываем на плане скоростей
9см. рис. 3б).
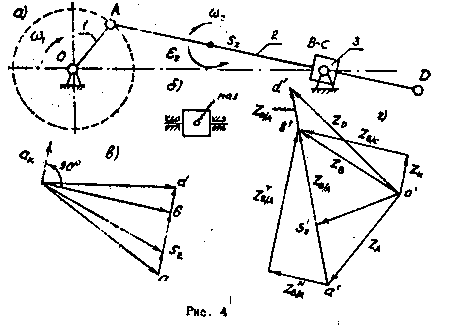
Кулисный механизм. Случай 2. В механизме, показанном на рис. 4а, точка В принадлежит кулисе 2, точка С - кулисному камню. В данный момент времени точки В и С совпадают. Скорость точки А определяется аналогично первым двум.
Составим уравнение для определения скорости точки В:
![]() .
(6)
.
(6)
Для решения этого уравнения необходимо знать направления скорости VB, для чего запишем второе уравнение:
![]()
 .
.
Переносная скорость точки VС равна нулю (точка С лежит на оси вращения кулисы 3). Относительная скорость VB/С направлена вдоль паза кулисы 3 (рис. 4б), т.е. вдоль АD, тогда
![]()
 =
=
![]() .
.
На плане скоростей (рис. 4в) откладываем отрезок оа, пропорциональный скорости точки А. Из точек о и а проводим направления скоростей VB и VB/А. Точка в определяет отрезки, пропорциональные скоростям VB и VB/А. Тогда VB = кV · ов, м/с; VB/А = кV · ав, м/с.
Скорости точек S2 и D определяются из отношений
![]() =
=
![]() ;
;
![]() =
=
![]() .
.
Откуда находим as2 и ad:
аs2 =
![]() ,
мм; аd =
,
мм; аd =
![]() ,
мм
,
мм
и откладываем их на
плане скоростей (рис. 4в). Соединив
полюс о с точками s2
и d, находим
![]() = кV · оs2, м/с; VD
= кV · оd, м/с.
= кV · оs2, м/с; VD
= кV · оd, м/с.
