
- •Разработчик методического комплекса профессор кафедры электрооборудования Евгений Иванович Цокур
- •Предисловие Данный конспект (его первая версия) представляет собой частично адаптированное к технологии дистанционного обучения изложение материала.
- •Раздел 1. Основы электротехники
- •Глава 1. Линейные электрические цепи постоянного тока
- •1.1. Основные понятия и определения
- •3. Линии передачи электрической энергии, которые связывают источники и приёмники.
- •4. Преобразователи энергии, которые включают в себя трансформаторы, выпрямители, а также различную коммутационную аппаратуру (выключатели, релейно-контакторные элементы автоматики и т.П.).
- •1.2. Электрический ток
- •1.3. Э.Д.С. И напряжение
- •1.4. Классификация электрических цепей
- •1.5. Электрическая цепь постоянного тока. Закон ома
- •1.6. Способы соединения сопротивлений
- •1.6.1 Последовательное соединение сопротивлений
- •1.6.2. Параллельное соединение сопротивлений
- •1.6.3. Смешанное соединение сопротивлений
- •1.7. Электрическая работа и мощность
- •Электрическая работа измеряется в джоулях, но согласно формуле
- •1.9. Расчет сложных электрических цепей
- •1.9.1 Применение законов Кирхгофа
- •1.9.2. Метод контурных токов
- •Тест № 1.2. Электрическое сопротивление и проводимость
- •Тест № 1.3 Параллельное соединение сопротивлений
- •Тест № 1.4. Параллельное соединение сопротивлений
- •Тест № 1.6 Смешанное соединение сопротивлений
- •Тест № 1.7. Расчет сложных электрических цепей
- •Примеры по расчету цепей постоянного тока Электрические цепи постоянного тока
- •Законы Кирхгофа.
- •Ток, потребляемый двигателем
- •Напряжение между главными проводами равно
- •Напряжение на параллельных ветвях
- •Глава 2. Магнитные цепи
- •2.1. Основные понятия и определения
- •2. Напряженность поля, (а/м), определяющая интенсивность и направление причины, которая создает магнитное поле (обычно это ток).
- •2.2. Характеристики ферромагнитных материалов
- •2.3. Намагничивание ферромагнитных материалов
- •2.4. Циклическое перемагничивание
- •2.5. Механические силы и работа тока в магнитном поле
- •2.6. Электромагнитная индукция
- •2.7. Электродвижущая сила, индуктируемая в катушке,
- •2.8. Индуктивность
- •Тест № 2.1. Циклическое перемагничивание
- •Глава 3. Основные понятия переменного тока
- •3.1. Определение, получение и изображение переменного тока
- •3.2 . Параметры переменного синусоидального тока
- •3.4. Однофазные электрические цепи
- •3.4.1. Особенности электрических цепей
- •3.4.2. Цепь с активным сопротивлением
- •3.4.3. Цепь с индуктивностью
- •3.4.4. Цепь с активным сопротивлением и индуктивностью
- •3.4.5. Цепь с емкостью
- •3.4.6. Цепь с активным сопротивлением и емкостью
- •3.4.7. Цепь с активным сопротивлением, индуктивностью и емкостью
- •3.4.8. Резонанс напряжений
- •В результате можно записать
- •Решая это уравнение относительно f , находим
- •3.4.9. Коэффициент мощности
- •Тест № 3.3. Цепь с активным сопротивлением и индуктивностью
- •Тест № 3.5. Цепь с активным сопротивлением, индуктивностью и емкостью
- •Тест № 3.6 Цепь с активным сопротивлением, индуктивностью и емкостью
- •Тест № 3.7. Резонанс напряжений
- •Примеры по цепям однофазного переменного тока
- •1. Период и частота переменного тока
- •2. Синусоидальные величины и их определение
- •Глава 4. Трехфазные электрические цепи
- •4.1. Принцип получения трехфазной э.Д. С.. Основные
- •4.2. Соединение трехфазной цепи звездой.
- •4.3. Соотношения между фазными и линейными
- •4.4. Назначение нулевого провода в четырехпроводной цепи
- •4.5. Соединение нагрузки треугольником. Векторные
- •4.6. Активная, реактивная и полная мощности
- •Тест 4.4. Назначение нулевого провода в четырехпроводной цепи
- •Тест 4.5. Выбор схем соединения осветительной и силовой нагрузок при включении их в трехфазную сеть
3.4.5. Цепь с емкостью
Проанализируем процессы в цепи, представленной на рис.43.
Рис. 43
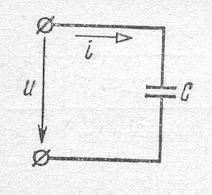
![]() ,
тогда ток в цепи также будет меняться
по синусоидальному закону. Величина
тока определяется по формуле
,
тогда ток в цепи также будет меняться
по синусоидальному закону. Величина
тока определяется по формуле![]() .
Количество электричестваq
на обкладках конденсатора связано с
напряжением на конденсаторе и его
емкостью: q
= C
u
.
.
Количество электричестваq
на обкладках конденсатора связано с
напряжением на конденсаторе и его
емкостью: q
= C
u
.
Следовательно,
 (3.27)
(3.27)
Таким образом, ток в цепи с емкостью опережает по фазе напряжение на угол π/2 (рис. 44 и рис. 45).
Физически
это объясняется тем, что напряжение на
конденсаторе возникает за счет разделения
зарядов на его обкладках в результате
протекания тока.
Следовательно,
напряжение появляется только после
возникновения тока
(сравните процесс появления напряжения
на конденсаторе с процессом увеличения
уровня жидкости при заполнении бака).
Выведем закон Ома для цепи с емкостью.
Из выражения (3.27) следует, что
![]() ,
или в иной форме
,
или в иной форме
![]() (3.28)
(3.28)
Введем обозначение:
![]() ,
(3.29)
,
(3.29)
где
![]() - емкостное сопротивление цепи.
- емкостное сопротивление цепи.
Тогда выражение закона Ома можно представить в виде: для амплитудных значений
![]() (3.30)
(3.30)
для действующих значений
![]() (3.31)
(3.31)
Рис. 44
Рис. 45
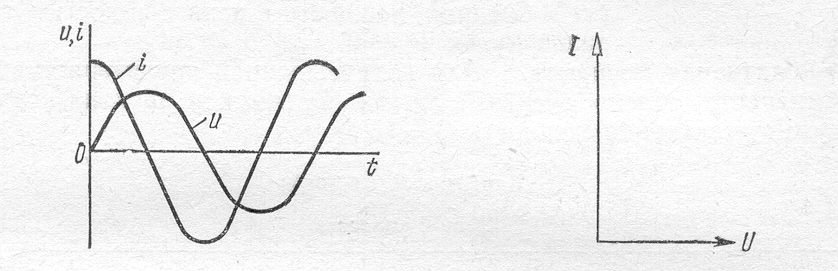
![]() уменьшается с ростом частоты. Это
объясняется тем, что при большей частоте
через поперечное сечение диэлектрика
в единицу времени протекает большее
количество электричества при том же
напряжении, что эквивалентно уменьшению
сопротивления цепи.
уменьшается с ростом частоты. Это
объясняется тем, что при большей частоте
через поперечное сечение диэлектрика
в единицу времени протекает большее
количество электричества при том же
напряжении, что эквивалентно уменьшению
сопротивления цепи.
Рис. 46
Рис. 47

Мгновенное
значение мощности.
Пусть начальная фаза тока в цепи равна
нулю, тогда
![]() .
Поскольку напряжение на емкости отстает
от тока на угол π/2 ,
.
Поскольку напряжение на емкости отстает
от тока на угол π/2 ,![]() или
или![]() .
Выражение для мгновенной мощности
примет вид
.
Выражение для мгновенной мощности
примет вид
![]() (3.32)
(3.32)
Анализ формулы (3.32) и графика рис. 47 показывает, что в цепи с емкостью, так же как и в цепи с индуктивностью, происходит переход энергии от источника к нагрузке, и наоборот. В данном случае энергия источника преобразуется в энергию электрического поля конденсатора. Из сравнения выражений (3.32) и (3.16) и соответствующих им графиков (рис. 47 и рис.42) видно, что если бы индуктивная катушка и конденсатор были включены последовательно, то между ними происходил бы обмен энергией. Средняя мощность в цепи с емкостью также равна нулю: Р = 0.
Реактивная мощность. Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность Q = UI.
3.4.6. Цепь с активным сопротивлением и емкостью
Рис. 48

![]() Тогда напряжение на активном сопротивлении
Тогда напряжение на активном сопротивлении![]() .
Напряжение на емкости отстает по фазе
от тока на угол π/2:
.
Напряжение на емкости отстает по фазе
от тока на угол π/2:![]() .
На основании приведенных выражений
построим векторную диаграмму для
этой цепи (рис. 49). Из векторной диаграммы
следует,
.
На основании приведенных выражений
построим векторную диаграмму для
этой цепи (рис. 49). Из векторной диаграммы
следует,
что
![]() .
Но
.
Но![]() ,
а
,
а
![]() ,
следовательно,
,
следовательно,
![]()
откуда
![]() .
(3.33)
.
(3.33)
Рис. 49
Рис. 50

![]() ,
выражение (3.33) можно записать в видеI
= U/z.
,
выражение (3.33) можно записать в видеI
= U/z.
Треугольник сопротивлений для рассматриваемой цепи показан на рис. 50. Расположение его сторон соответствует расположению сторон треугольника напряжений на векторной диаграмме рис. 49. Угол сдвига фаз φ в этом случае будет отрицательным, тик как напряжение отстает по фазе от тока:
![]() ,
(3.34)
,
(3.34)
![]() (3.35)
(3.35)
В энергетическом отношении цепь с r и С формально не отличается от цепи с r и L. Покажем это.
Мгновенное значение мощности. Так как фаза тока принята нулевой:
![]() ,
напряжение отстает по фазе от тока на
угол
,
напряжение отстает по фазе от тока на
угол![]() и, следовательно,
и, следовательно,![]() .
Тогда:
.
Тогда:
![]() .
.
Опуская промежуточные преобразования, получим
![]() (3.36)
(3.36)
Средняя мощность. Средняя мощность определяется постоянной составляющей мгновенной мощности:
![]() .
.
Реактивная мощность. Реактивная мощность характеризует интенсивность обмена энергией между источником и емкостью:
Q = UI sin φ.
Так как φ < 0, реактивная мощность Q отрицательна. Физически это означает, что когда емкость отдает энергию, индуктивность ее потребляет, если они находятся в одной цепи.
