3.4.4. Цепь с активным сопротивлением и индуктивностью

Цепь (рис. 39) состоит из участков, свойства которых известны. Проанализируем работу данной цепи. Пусть ток в цепи изменяется по закону . Тогда напряжение на активном сопротив­лении, так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке будет выражаться соот­ношением, поскольку на индуктивности напряжение опережает по фазе ток на угол π/2. Построим векторную диаграмму для рассматриваемой цепи (рис. 40). Сначала отклады­ваем вектор тока, затем вектор напряжениясовпадающий по фазе с током. Вектор, опережающий ток на угол π/2, приставим к век­тору, для удобства их сложения. Суммарное напряжение иизображается векторомсдвинутым по фазе от­носительно тока на угол φ. Векторы,иобразуют так назы­ваемый треугольник напряжений. Выведем закон Ома для этой цепи. На основании теоремы Пифагора для треугольни­ка напряжений имеем. Но=Ir , а , следовательно,

откуда

(3.18)

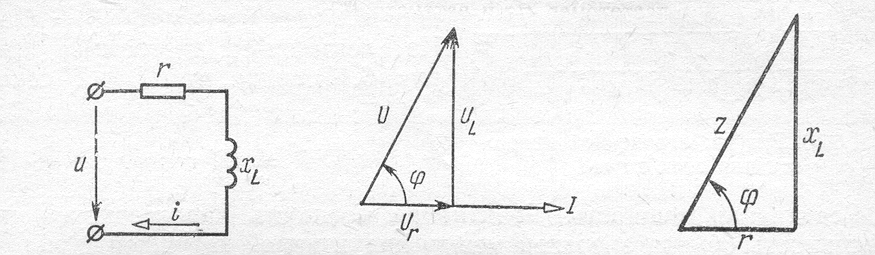
Рис. 39 Рис. 40 Рис. 41

Введем обозначение:, гдеz - полное сопротивление цепи.

Тогда выражение закона Ома примет вид

(3.19)

Так как полное сопротивление цепи z определяется по теореме Пифагора, ему соответствует треугольник сопротивлений (рис.41). Поскольку при последовательном соединении напряжения на участ­ках прямо пропорциональны сопротивлениям, треугольник сопротивлений подобен треугольнику напряжений. Угол сдвига фаз φ между током и напряжением определяется из треугольника сопро­тивлений:

, (3.20)

. (3.21)

Для последовательной цепи условимся отсчитывать угол φ от век­тора тока. Поскольку вектор сдвинут по фазе относительно тока на угол φ против часовой стрелки, этот угол имеет положительное значение. В дальнейшем покажем, что знак угла φ определяется по формальному признаку.

Выведем энергетические соотношения для цепи с активным сопро­тивлением и индуктивностью.

Мгновенное значение мощности. Мгновенное значение мощности выражается соотношениями:

или

(3.22)

Рис. 42

Анализ выражения (3.22) и графика рис. 42, построенного на его основе, показывает, что мгновенное значение мощности колеб­лется около постоянного уровня , который определяет сред­нюю мощность. Отрицательная часть графика определяет энергию, которая переходит от источника к индуктивной катушке и обратно.

Средняя мощность. Средняя, или активная, мощность для дан­ной цепи характеризует расход энергии на активном сопротивле­нии и, следовательно, . Из векторной диаграммы (см. рис.40) видно, что. Тогда

. (3.23)

Реактивная мощность. Реактивная мощность характеризует ин­тенсивность обмена энергией между индуктивной катушкой и источ­ником

. (3.24)

Полная мощность. Полная мощность применяется для оценки пре­дельной мощности электрических машин:

. (3.25)

Так как , то

(3.26)

Единицей измерения полной мощности является вольт-ампер (ВА).