Тест № 2.1. Циклическое перемагничивание

Вопросы		Варианты ответа	Выбран вариант
	1.Может ли петля гистерезиса иметь вид, показанный на графике?	Может
		Не может
	2.Из рассмотрения петли гистерезиса следует, что при Н=Нс В=0. Означает ли это, что:	Магнитные поля катушки и сердечника равны нулю?
		Магнитные поля катушки и сердечника равны по величине, но направлены в разные стороны?
		Магнитное поле сердечника отсутствует, магнитное поле катушки не равно нулю?
	3.Затрачивается ли энергия для перемагничивания материала, представленного данной кривой?	Затрачивается
		Не затрачивается
		Для ответа недостаточно данных

Глава 3. Основные понятия переменного тока

3.1. Определение, получение и изображение переменного тока

Цепи с изменяющимися токами  переменными токами по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются тем, что переменные токи и напряжения отдельных элементов электротехнических устройств порождают в них переменные электрические и магнитные поля. В результате изменения этих полей в электрической цепи возникают явления самоиндукции, взаимной индукции и токов смещения, которые оказывают существенные влияния на протекающие в цепи процессы и анализ их усложняется.

Процессы в линейных цепях с токами и напряжениями, изменяющимися по синусоидальным законам, являются простейшими.

Переменным называется ток, изменение которого по величине и на­правлению повторяется периодически через равные промежутки времени.

Рис. 22

Электрические цепи в которых величина и направление напряжения и тока периодически изменяются во времени по синусоидальному закону называются синусоидальными (рис.22).

Рис. 23

Синусоидальный ток нашел широкое применение в различных областях техники, что объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока (рис.23), надежностью их работы и удобством эксплуатации. Переменный ток (в дальнейшем имеется ввиду синусоидальный ток) одного напряжения легко преобразовать в переменный ток другого напряжения, используя трансформатор, что очень важно при передаче электрической энергии на большие расстояния. В случае необходимости, напряжение переменного тока достаточно просто преобразовать в напряжение постоянного тока с помощью полупроводниковых выпрямителей.

3.2 . Параметры переменного синусоидального тока

Для количественной характеристики переменного тока служат следующие параметры:

1. Мгновенные значения тока i, напряжения u, э.д.с. е - их значения в любой момент времени:

2. Амплитудные значения тока , напряжения, э.д.с.- максимальные значения мгновенных величинi , u и е (рис.24).

3. Период Т - промежуток времени, в течение которого ток совершает полное колебание и принимает прежнее по величине и знаку мгновенное значение. Период измеряется в секундах (с), миллисекун­дах (мс) и микросекундах (мкс).

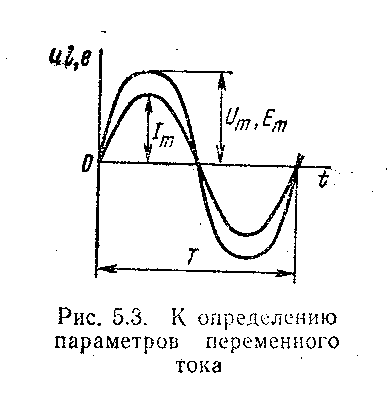
Рис. 24 Рис. 25

4. Угловая частота , характеризующая скорость вра­щения катушки генератора в магнитном поле (рис. 23). На практике для полу­чения нужной частоты при относительно малой скорости вращения генераторы имеют несколько пар полюсовр.

На рис. 25 показан генератор с двумя парами полюсов NS, в котором за один оборот катушки э. д. с. изменяет направление 4 раза или 2 р раз. Следовательно, одному обороту катушки соответствует р перио­дов переменного тока. Введем понятие электрического угла ;

= а.

Тогда угловая частота будет определять электрическую угловую скорость вращения катушки:

, (3.1)

где р2π - электрический угол, соответствующий одному обороту ка­тушки в пространстве; рТ - время, соответствующее р периодам тока.

Таким образом, формула (3.1) определяет электрическую угловую скорость или угловую частоту.

5. Циклическая частота ƒ - величина, обратная периоду Т:

ƒ = 1/Т, (3.2)

показывающая число полных колебаний тока за 1 с.

Единицей измерения циклической частоты является герц (Гц).

1 Гц = 1/с.

Промышленной частотой в России считается частота 50 Гц. Рас­пространены также следующие производные единицы измерения цик­лической частоты: килогерц (кГц), мегагерц (мГц) и гигагерц (гГц). 1 кГц = 10Гц.

1 мГц = 10Гц ; 1 гГц = 10Гц.

Сопоставляя формулы (3.1) и (3.2), получаем

ω = 2πƒ. (3.3)

а б

Рис. 26

6. Действующие значения тока I, напряжения U и э.д.с. Е. Для измерения переменного тока, напряжения и э.д.с. вводится понятие действующего значения. Переменный ток сравнивают с постоянным по тепловому действию. Это иллюстрируется рис. 26. Если положение реостатов подобрано так, что количество тепла, выделяемого в схемах рис. 26, а и 26, б на сопротивлении R , ока­зывается одинаковым, то можно считать, что и токи в схемах будут одинаковыми. Таким образом, действующие значение переменного тока равно такому постоянному току, который за время, равное одному периоду, выделяет на данном сопротивлении одинаковое количество тепла с переменным током.

Найдем соотношение между действующим и амплитудным значе­ниями тока. Согласно определению q_пос = q_пер (q_пос,,q_пер- соответственно количество тепла, выделяемого постоянным и переменным током)

q_пос и q_пер

где - количество тепла, выделяемого переменным током за времяdt.

Приравнивая эти выражения, получаем

Сокращая на общий множитель R и учитывая, что , находим выражение для действующего значения тока

,

или после интегрирования

(3.4)

Аналогично определяются и действующие значения э.д.с. и напряжения

E =E_m/ U=U_m/.

7. Фаза переменного тока

а б

Рис. 27

Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ, как показано на рис. 27, а. При вращении якоря в витках будет наводиться э.д.с. индукции одинаковой частоты ω и амплитуды (рис. 27,б), так как витки вращаются с одинаковой угловой скоростью в одном и том же магнит­ном поле.

Положение витков задано углами идля произвольного мо­мента времени, которое можно положитьt = 0. Плоскости витков не совпадают с нейтральной плоскостью 00'. Мгновенные значения э.д.с. как функции времени будут определяться выражениями:

(3.5)

Следовательно, в момент t = 0 э. д. с. не равны нулю:

Электрические углы иопределяют значения э.д.с. в начальный момент времени и называются начальными фазовыми углами или начальными фазами.

Так как начальные фазы этих э.д.с. различны, максимальные значения э.д.с. в витках наступают не одновременно, а с определенным сдвигом во времени. Временной сдвиг определяется разностью начальных фаз и называется углом сдвига фаз или сдвигом фаз φ (рис. 27, б)

φ = –(3.6)

Временной сдвиг ∆t определяют в соответствии с равенством α = ωt

. (3.7)

В данном случае одна из э.д.с. является опережающей, а другая - отстающей по фазе. Будем считать опережающей ту э.д.с., макси­мум которой расположен левее, при условии φ < π. Угол φ опре­деляют по расстоянию между ближайшими максимумами э.д.с. одного знака или моментами прохождения нулевого значения.

8. Изображение синусоидальных величин с помощью векторов

При расчете цепей переменного тока часто приходится произво­дить операцию сложения и вычитания токов и напряжений. Когда токи и напряжения заданы аналитически или временными диаграмма­ми, эти операции оказываются весьма громоздкими. Существует метод построения векторных диаграмм, который позволяет значительно упростить действия над синусоидальными величинами. Покажем, что синусоидальная величина может быть изображена вращающимся (с угловой скоростью ω) вектором.

Изображение синусоидальных величин с помощью векторов дает возможность нагляд­но показать начальные фазы этих величин и фазовый сдвиг между ними.

Рис. 28

На векторных диаграммах длины векто­ров соответствуют действующим значениям тока, напряжения и э.д.с., так как они пропорциональны амплитудам этих величин.

На рис. 28 показаны векторы и, с начальными фазами соответственноии фазовым сдвигом.

Совокупность нескольких векторов, соответствую­щих нулевому моменту времени, называется векторной диаграммой.