
3. Волны в диэлектриках
В
диэлектриках
![]() ,
поэтому
можно приближенно положить
,
поэтому
можно приближенно положить
![]() .
Тогда получаем:
.
Тогда получаем:
![]() (25)
(25)
Находим
: (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
Из
полученных результатов следует, что
параметры волны (![]() ),
распространяющейся
в реальном диэлектрике, мало отличаются
от ее параметров в среде без потерь с
теми же
),
распространяющейся
в реальном диэлектрике, мало отличаются
от ее параметров в среде без потерь с
теми же
![]() .
Коэффициент ослабления
.
Коэффициент ослабления
![]() является малой величиной и в первом
приближении не зависит от частоты.
Дисперсионные свойства проявляются
незначительно.
является малой величиной и в первом
приближении не зависит от частоты.
Дисперсионные свойства проявляются
незначительно.
4. Волны в проводниках
В
проводниках (например, в металлах)
![]() .
Поэтому
в выражениях для
.
Поэтому
в выражениях для
![]() можно пренебречь единицей по сравнению
с
можно пренебречь единицей по сравнению
с
![]() .
В результате получим
.
В результате получим
![]() (29)
(29)
Постоянные
![]() нелинейно зависят от частоты. Следовательно,
свойства волны на разных частотах будут
существенно различаться. Формулы для
фазовой скорости, длины волны и
характеристического сопротивления в
этом случае принимают вид
нелинейно зависят от частоты. Следовательно,
свойства волны на разных частотах будут
существенно различаться. Формулы для
фазовой скорости, длины волны и
характеристического сопротивления в
этом случае принимают вид
![]() (30)
(30)
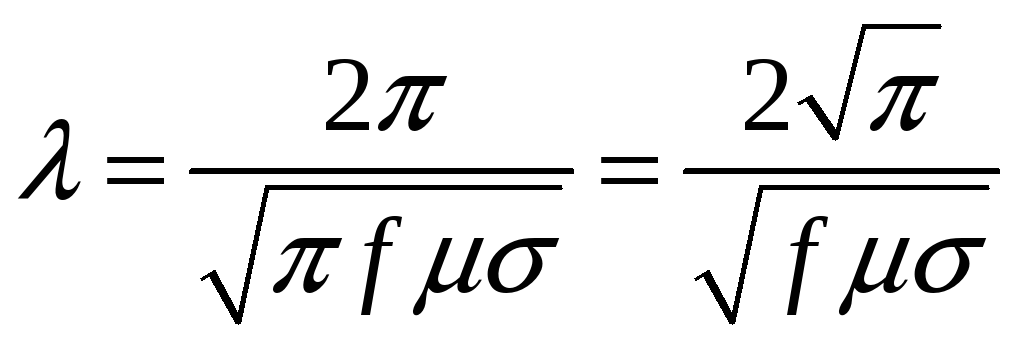 (31)
(31)
![]() (32)
(32)
Сравним
параметры плоских волн, распространяющихся
в вакууме и в меди (![]() )
на частоте 1
Мгц.
)
на частоте 1
Мгц.
в вакууме: в металле:
![]() ;
;
![]() ;
;
![]() м;
м; ![]() м;
м;
![]() ;
; ![]() .
.
5. Затухание волн
Коэффициент
ослабления
![]() волны, распространяющейся в проводнике,
большая величина. Поэтому амплитуды
векторов поля резко уменьшаются вдоль
направления распространения: волна
быстро затухает. Пусть амплитуда
напряженности электрического поля в
точке с координатой
волны, распространяющейся в проводнике,
большая величина. Поэтому амплитуды
векторов поля резко уменьшаются вдоль
направления распространения: волна
быстро затухает. Пусть амплитуда
напряженности электрического поля в
точке с координатой
![]() равна
равна
![]() ,
а
амплитуда в точке с координатой
,
а
амплитуда в точке с координатой
![]() равна
равна
![]() .
Отношение
.
Отношение
![]() (33)
(33)
показывает,
во сколько раз уменьшилась амплитуда
волны при прохождении ею расстояния
![]() .
.
Затухание
измеряют в неперах (Нп) и децибелах (дБ).
Затухание в неперах определяют как
натуральный логарифм отношения (33)
![]() .
Затухание
в децибелах определяют как двадцать
десятичных логарифмов того же отношения:
.
Затухание
в децибелах определяют как двадцать
десятичных логарифмов того же отношения:
![]() ,
т.е.
,
т.е.
![]() .
Коэффициент
.
Коэффициент
![]() ,
таким образом, определяет затухание
волны при прохождении ею пути в один
метр и измеряется в неперах на метр
(Нп/м).
,
таким образом, определяет затухание
волны при прохождении ею пути в один
метр и измеряется в неперах на метр
(Нп/м).
Вычислим
затухание волны, распространяющейся в
меди, при частоте в 1
Мгц.
Коэффициент ослабления
![]() Нп/м. Это означает, например, что при
прохождении волной расстояния в один
миллиметр ее амплитуда уменьшается в
Нп/м. Это означает, например, что при
прохождении волной расстояния в один
миллиметр ее амплитуда уменьшается в
![]() раз,
т.е. примерно в 2,67 миллиона раз. Приведенный
пример показывает, что переменное
электромагнитное поле на частотах
радиотехнического диапазона практически
не проникает в глубь проводника.
раз,
т.е. примерно в 2,67 миллиона раз. Приведенный
пример показывает, что переменное
электромагнитное поле на частотах
радиотехнического диапазона практически
не проникает в глубь проводника.
6. Глубина проникновения
Расстояние
![]() ,
при прохождении которого электромагнитное
поле ослабевает в
,
при прохождении которого электромагнитное
поле ослабевает в
![]() раз, называют
глубиной проникновения поля в среду.
На расстоянии
раз, называют
глубиной проникновения поля в среду.
На расстоянии
![]() ослабление составляет 1 Нп, т.е.
ослабление составляет 1 Нп, т.е.
![]() и, следовательно,
и, следовательно,
![]() (34)
(34)
В случае металла выражение (34) упрощается:
![]() (35)
(35)
Как
видно из формулы (35), глубина проникновения
от частоты: чем больше частота, тем
меньше
![]() .
.
