
- •Технических систем
- •Общие методические указания
- •Использование закономерностей
- •Распределение параметров по наработке
- •Расчет параметров распределения ресурса деталей автомобиля по результатам инженерных наблюдений
- •Значения ресурса l , тыс. Км
- •Шкала интервалов и частота попадания в интервал
- •Параметры распределения
- •Определение статистики 2
- •Вариационный ряд значений ресурса l, тыс. Км (значения расставлены по возрастанию)
- •Шкала интервалов и частота попадания в интервал
- •Расчетные параметры распределения
- •Объединенный интервальный ряд
- •Расчет статистики 2
- •Расчет показателей эффективности
- •Станции технического обслуживания
- •Автомобилей
- •Как системы массового обслуживания
- •Параметры сто
- •Решение
- •Решение
- •Решение
- •Нормированная функция нормального распределения
- •Плотность вероятности нормального распределения
- •И числа степеней свободы k
- •Значение функции
- •О главление
Шкала интервалов и частота попадания в интервал
|
Номер интервала |
Границы интервалов, тыс. км |
Середины интервалов lr , тыс. км |
Частота попадания в интервал, ni |
|
|
|
|
|
г) по данным табл. 2.2 строится гистограмма fn(l) (рис. 2.1). Для ее построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервал варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой.
Определить параметры и характеристики закона распределения. Для нормального закона распределения плотность вероятности имеет вид
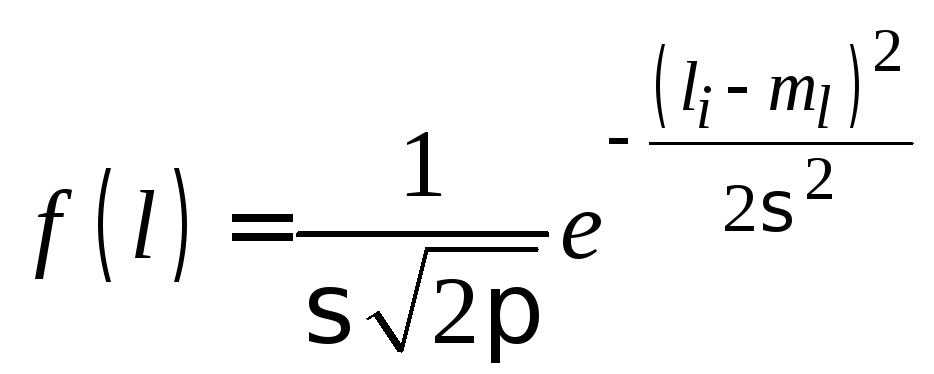 .
.
Статистические характеристики теоретического распределения
оцениваются по результатам испытаний:
– математическое ожидание (для интервального вариационного
ряда, табл. 2.2)
![]() ,
,
где
![]() –
середины интервалов,r
– количество интервалов;
–
середины интервалов,r
– количество интервалов;
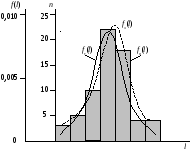
Рис. 2.1
– среднеквадратическое отклонение (для интервального вариаци-
онного ряда, табл. 2.2)
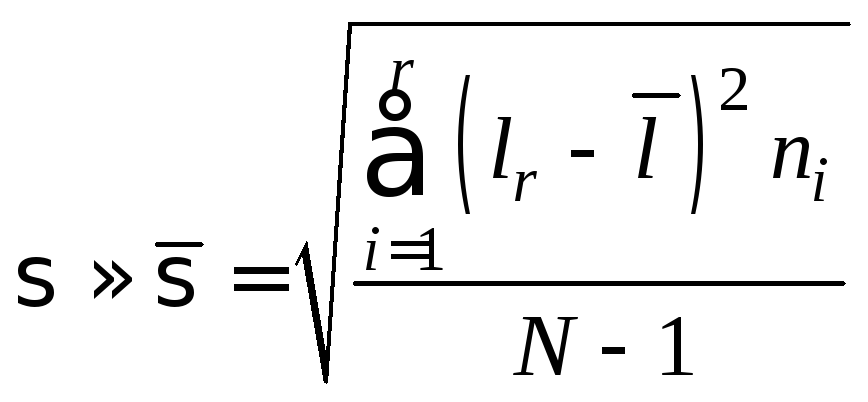 ;
;
– значения эмпирической плотности распределения вероятностей
![]() по интервалам
наработки (табл. 2.3)
по интервалам
наработки (табл. 2.3)
![]() ;
;
– нормированные и центрированные отклонения середины интер-
валов
![]() (табл. 2.3)
(табл. 2.3)
![]() ;
;
– значения теоретической плотности распределения вероятностей
(табл. 2.3)
![]() ,
,
где
![]() – плотность вероятности нормального
– плотность вероятности нормального
распределения (табл. П2 Приложения).
Результаты расчета представляются в табл. 2.3.
Т а б л и ц а 2.3
Параметры распределения
|
|
|
|
|
|
|
|
|
|
|
|
По результатам
табл. 2.3 строятся графики
![]() и
и![]() ,
,
которые совмещаются с построенной ранее гистограммой (рис. 2.1).
Проверить согласие между эмпирическим и теоретическим (нор-
мальным)
распределениями по критерию
![]() Пирсона
Пирсона
![]() ,
,
где
![]() – эмпирические и теоретические частоты
попадания случайной величины вi-й
интервал соответственно; n
= N
.
– эмпирические и теоретические частоты
попадания случайной величины вi-й
интервал соответственно; n
= N
.
Правило применения
критерия 2
сводится к следующему. Рассчитав значение
2
и выбрав уровень значимости критерия
![]() ,
по
таблицам2-распределения
(табл. П3 Приложения) определяют
,
по
таблицам2-распределения
(табл. П3 Приложения) определяют
![]() ,
где
,
где![]() –
число степеней свободы,r
– количество интервалов, s
– количество параметров распределения
(для нормального распределения s
= 2). Если
–
число степеней свободы,r
– количество интервалов, s
– количество параметров распределения
(для нормального распределения s
= 2). Если
![]() >
>![]() ,
то проверяемую гипотезу отвергают; если
,
то проверяемую гипотезу отвергают; если![]()
![]()
![]() ,
то гипотезу принимают.
,
то гипотезу принимают.
Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее пяти наблюдений. Если количество наблюдений в отдельных интервалах меньше пяти, интервалы объединяются.
Вероятность
![]() определяется следующим образом.
Вероятностьр1
выражает вероятность того, что случайная
величина Х,
имеющая нормальный закон распределения,
принимает значение, принадлежащее
интервалу (l1
– l2),
т.е.
определяется следующим образом.
Вероятностьр1
выражает вероятность того, что случайная
величина Х,
имеющая нормальный закон распределения,
принимает значение, принадлежащее
интервалу (l1
– l2),
т.е.
![]()
![]() ,
,
где
![]() – функция
Лапласа (табл. П4 Приложения). Аналогично
вычисляются остальные рi.
– функция
Лапласа (табл. П4 Приложения). Аналогично
вычисляются остальные рi.
Для нахождения статистики 2 составляется табл. 2.4. Далее делается заключение о согласии эмпирического и теоретического законов распределения.
Т а б л и ц а 2.4
