Использование закономерностей

СЛУЧАЙНЫХ ПРОЦЕССОВ ИЗМЕНЕНИЯ

ТЕХНИЧЕСКОГО СОСТОЯНИЯ АВТОМОБИЛЕЙ

ПРИ РАСЧЕТЕ ПОКАЗАТЕЛЕЙ ТЭА

1.1. Определить вероятность отказа детали при исходных данных, приведенных в табл. 1.1. Распределение наработки детали до отказа подчиняется нормальному закону.

Т а б л и ц а 1.1

Параметры распределения

Номер строки	Интервал пробега	Математическое ожидание тl (тх) (среднее значение )	Среднее квадратическое отклонение
	тыс. км
1	0…60	85	25
2	60…120	86	26
3	0…80	87	27
4	80…125	88	28
5	0…75	89	29
6	75…140	90	30
7	0…85	91	31
8	70…130	92	32
9	0…90	94	33
0	90…150	95	34
	е	д	е

П Р И М Е Р

1 - 1

Определить вероятность первой замены (отказа) детали при работе автомобиля с начала эксплуатации до наработки 70 000 км. Распределение наработки до первого отказа подчиняется нормальному закону с параметрами: км,км.

Решение

Используя понятие нормированной функции, определим нормированное отклонение:

.

Тогда P(x) = Ф(z) = Ф(– 0,83). Из табл. П1 Приложения находим

Ф(– 0,83)0,20.Ответ

Таким образом, примерно 20 % автомобилей потребуют замены

деталей при пробеге с начала эксплуатации до 70 000 км.

П Р И М Е Р

1 - 2

Определить вероятность отказа той же детали (ПРИМЕР 1-1) в интервале пробега от х₁= 70 000 км дох₂= 125 000 км.

Решение

z₁= – 0, 83;z₂= (125 000 – 95 000)/30 000 = 1.

По табл. П1 Приложения находим:

Ф(– 0,83) = 0,20; Ф(1) = 0,84.

Таким образом, в интервале пробега 70 000…125 000 км вероят-

ность отказа детали составляет

Ф(z₂) – Ф(z₁) = 0,64,Ответ

т.е. у 64 автомобилей в этом интервале пробега произойдет отказ детали и потребуется ее замена или ремонт.

1.2. На основе закономерностей процессов восстановления определить возможное число замен накладок сцепления при пробеге автомобиля х (тыс. км) и исходных данных, приведенных в табл. 1.2.

Рассмотреть два случая:

1) вероятность (пример 1-3),

2) вероятность (табл. 1.2, пример 1-4).

Т а б л и ц а 1.2

Распределение параметров по наработке

Номер строки	Пробег автомобиля х	Наработка до первой замены	Среднее квадратическое отклонение 	Коэффициент восстановления ресурса 	Вероятность
	тыс. км			–	–
1	120	40	8	0,5	0,80
2	125	45	9	0,6	0,85
3	130	50	10	0,7	0,90
4	135	55	11	0,5	0,95
5	140	60	12	0,6	0,80
6	145	43	13	0,7	0,85
7	150	46	14	0,5	0,90
8	155	52	15	0,6	0,95
9	160	57	16	0,7	0,80
0	165	62	17	0,6	0,90
	е	е	д	г	д

П Р И М Е Р

1 - 3

Наработка до первой замены накладок сцепления тыс. км, среднее квадратическое отклонениетыс. км, коэффициент восстановления ресурса.

Определить возможное число замен при пробеге автомобиля 150 тыс. км.

Решение

Для расчетов используем формулу

.

Используя табл. П1 Приложения последовательно определяем Q₁,Q₂,Q₃ и т.д.

;

;

Q₃(150) = 0,995;Q₄(150) = 0,69;

Q₅(150) = 0,136;Q₆(150) = 0,007.

Поскольку Q₆мало, последующие расчеты дляQ₇и других можно не производить.

Таким образом, к пробегу 150 тыс. км возможное число замен

данной детали составит

. Ответ

Если использовать формулу

,

получим следующую оценку ведущей функции параметра потока отказов при пробеге автомобилях= 150 тыс. км:

. Ответ

Таким образом, к пробегу х= 150 тыс. км в среднем по этой

формуле возможно от 3,3 до 4,3 отказов сцепления.

П Р И М Е Р

1 - 4

Наработка до первой замены накладок сцепления тыс. км, среднее квадратическое отклонениетыс. км, коэффициент восстановления ресурса. Определить с достоверностьюнеобходимое число накладок сцепления на пробег автомобиля 150 тыс. км.

Решение

Так как условия задачи требуют обеспечения накладками с вероятностью 90 %, то необходимо определить верхнюю границу потребности в накладках за 150 тыс. км пробега.

Прежде всего определим нормированное отклонение при

–из табл. П1 Приложения имеем . Верхняя

граница потребности в деталях составит

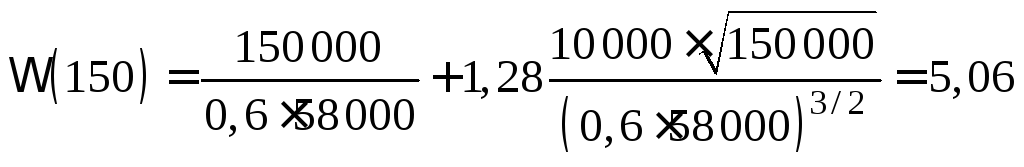. Ответ

Следовательно, с вероятностью 90 % можно полагать, что за

150 тыс. км пробега потребуется не более 5 комплектов накладок

сцепления. Нижняя граница составит 3,54 комплекта.

Таким образом, используя значения параметра потока отказов,

можно определить конкретный расход деталей за любой заданный

период и планировать работу системы снабжения.

З А Д А Ч А 2