Задание для самостоятельной работы

1. Какие поверхности определяются следующими уравнениями (сделайте чертеж)

Ответ: а) круговой цилиндр ;

б) параболический цилиндр с образующими параллельными оси ;

в) эллиптический цилиндр;

г) параболический цилиндр с образующим параллельными оси ;

д) пара плоскостей, не рассекающихся по оси ;

е) гиперболический цилиндр, образующие параллельными оси .

2. Составьте уравнение кругового конуса, образованного вращением прямой вокруг оси.

Ответ: .

3. Составьте уравнение двуполостного гиперболоида вращения вокруг оси (сделайте чертеж).

Ответ: .

4. Составьте уравнение поверхности, образованной вращением параболы

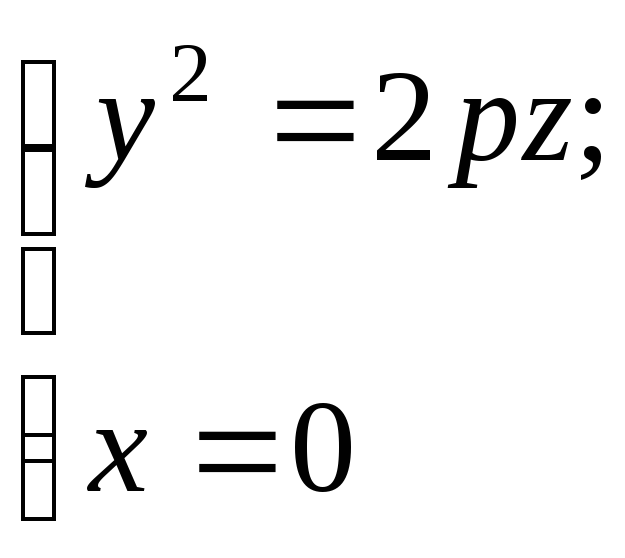
вокруг оси (сделайте чертеж).

Ответ: .

5. Составьте уравнение эллипсоида вращения вокруг оси (сделайте чертеж).

Ответ: .

6. Методом сечений исследуйте форму и расположение относительно системы координат следующих поверхностей (сделайте чертеж):

Ответ: а) односторонний гиперболоид; в) эллипсоид;

б) эллиптический параболоид; г) двуполостный гиперболоид.

7. Выделением полных квадратов и переносом начала координат упростите уравнение поверхностей:

Ответ: а) сфера;

б) однополостный гиперболоид;

в) двуполостный гиперболоид;

г) эллипсоид;

д) гиперболоид параболический;

е) эллиптический гиперболоид;

ж) двуполостный гиперболоид.

8. Запишите уравнение проекции на координатную плоскость линии пересечения эллиптического параболоидаплоскостьюи, приведя его к каноническому виду, установите, какую линию оно задает.

Ответ: эллипс.

9. В каких точках прямая пересекает эллипсоид

Ответ: и.

10. Докажите, что прямая лежит на однополостным гиперболоиде

11. Составьте уравнение множества точек, расположенных вдвое ближе к точке , чем к точке.

Ответ: .

117