Поверхности второго порядка

§ 7. Цилиндрические и конические поверхности. Поверхности вращения

Основные теоретические сведения

Цилиндрической поверхностью или просто цилиндром называется всякая поверхность, которую можно получить движением прямой, перемещающийся параллельно некоторому вектору и все время пересекающей данную линию, которая носит название направляющей. Движущаяся прямая называется образующей.

Конической поверхностью или просто конусом называется поверхность, образованная движением прямой, проходящей через данную точку, называемую вершиной конуса, и скользящей по данной кривой. Движущаяся прямая называется образующей конуса, а кривая, по которой скользит образующая, - направляющей.

Вращением фигуры вокруг данной прямой (оси вращения)называется такое движение, при котором каждая точка фигуры описывает окружность с центром на оси вращения, лежащую в плоскости, перпендикулярной к оси вращения.

Поверхность, образованная вращением линии вокруг оси, называется поверхностью вращения.

Канонические уравнения поверхностей второго порядка

Поверхность второго порядка задается в прямоугольных координатах уравнением второй степени

(7.1)

Путем преобразования координат (поворотом осей и параллельным переносом) уравнение (7.1) приводится к каноническому виду. В случае, когда в уравнении (7.1) отсутствуют члены с произведением координат , это уравнение выделением полных квадратов по,,и параллельным переносом осей координат приводится к каноническому виду подобно тому, как это делалось для линий второго порядка (см. Исследование общего уравнение линии второго порядка). Поверхности второго порядка и их канонические уравнения представлены в табл. 3.

Форму и расположение поверхностей второго порядка обычно изучают методом параллельных сечений. Сущность метода заключается в том, что поверхность пересекается несколькими плоскостями, параллельными координатным плоскостям. Форма и параметры полученных сечений позволяют выяснить форму самой поверхности.

Таблица 3

Поверхность второго порядка, каноническое уравнение	Вид
1	2
Эллипсоид

1	2
Гиперболоид: однополостный, двуполостный,
Конус,
Параболоид: эллиптический, гиперболический,

1	2
Цилиндр: эллиптический, гиперболический, параболический,

Примеры решения задач

Задача 7.1. Составить уравнение сферы, радиус которой , а центр находится в точке.

Решение. Сфера – это множество точек, отстоящих от центра на одном и том же расстоянии. Следовательно, обозначив через координаты произвольной точкисферы и выразив через них равенство, будем иметь

.

Возведя обе части равенства в квадрат, получим искомое каноническое уравнение сферы:

.

Если центр сферы поместить в начало координат, то уравнение сферы имеет более простой вид:

.

Ответ. .

Задача 7.2. Составить уравнение конической поверхности с вершиной в начале координат и направляющей

(7.1)

Решение. Канонические уравнения образующих через точку и точкунаправляющей, имеет вид

(7.2)

Исключим ,,из уравнений (7.1) и (7.2). Для этого в уравнениях (7.2) заменимнаи определими:

;

Подставив эти значения ив первое уравнение системы (7.1), будем иметь:

или

Полученное уравнение определяет конус второго порядка (см. табл. 3)

Задача 7.3. Какую поверхность определяет уравнение

Решение. Эта поверхность есть гиперболический цилиндр с образующими, параллельными оси Действительно, данное уравнение не содержит, а направляющая цилиндра есть гипербола

с центром симметрии в точке и действительной осью, параллельной оси.

Задача 7.4. Исследовать и построить поверхность, заданную уравнением

Решение. Пересечем поверхность плоскостью . В результате имеем

откуда . Это уравнение параболы в плоскости

Сечение заданной поверхности плоскостью есть парабола

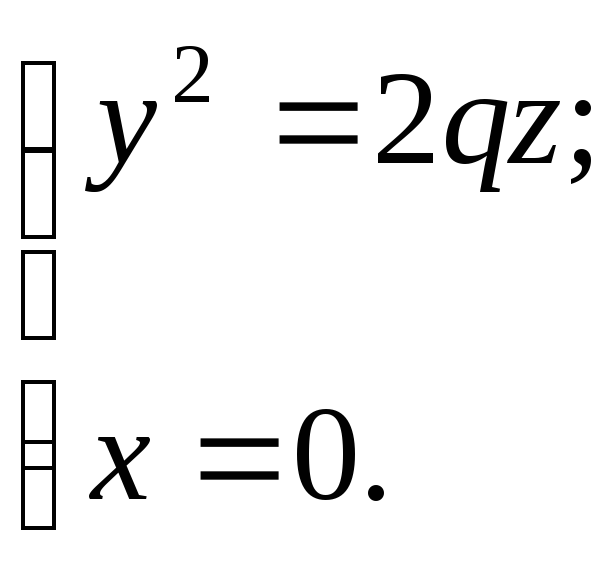
Сечение плоскостью есть пара пересекающихся прямых:

Сечение плоскостями, параллельными плоскости , есть гиперболы:

При действительная ось гиперболы параллельна оси, приоси. Исследуемая поверхность является гиперболическим параболоидом (по ассоциации с формой, поверхность получила название "седло").

Замечание. Интересным свойством гиперболического параболоида является наличие прямых линий, лежащих всеми своими точками на его поверхности. Такие прямые называются прямолинейными образующими гиперболического параболоида. Через каждую точку гиперболического параболоида проходят две прямолинейные образующие.

Задача 7.5. Какую поверхность определяет уравнение

Решение. Чтобы привести данное уравнение к каноническому виду, выделим полные квадраты переменных ,,:

Отсюда

Сравнивая полученное уравнение с табличными (см. табл. 3), видим, что это уравнение однополостного гиперболоида, центр которого смещен в точку Путем параллельного переноса системы координат по формулам

приведем уравнение к каноническому виду:

Замечание. Однополостный гиперболоид, как и гиперболический, имеет два семейства прямолинейных образующих.