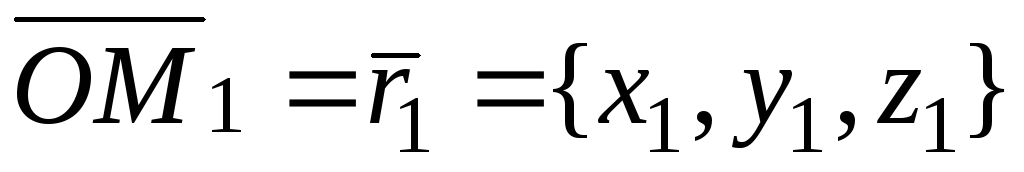- •§5. Линейные образы на плоскости
- •Если , то из векторного уравненияполучим
- •§6. Взаимное расположение двух прямых
- •§7. Определение расстояния от точки до прямой
- •§8. Пучок прямых на плоскости
- •§9. Линейные образы в пространстве
- •Доказательство аналогично доказательству для прямой/
- •Приведение общих уравнений прямой к
- •Пусть прямая определена общими уравнениями
- •§13. Взаимное расположение двух прямых
- •§14. Расстояние между скрещивающимися прямыми
Действительно,
если точка
![]() принадлежит поверхности, определяемой
уравнением
принадлежит поверхности, определяемой
уравнением![]() ,
то координаты точки
,
то координаты точки![]() удовлетворяют этому уравнению:
удовлетворяют этому уравнению:![]() .
Тогда этому уравнению удовлетворяют
координаты точки
.
Тогда этому уравнению удовлетворяют
координаты точки![]() ,
где
,
где![]() - любое число. Но точка
- любое число. Но точка![]() с такими координатами есть любая точка
прямой, которая проходит через точку
с такими координатами есть любая точка
прямой, которая проходит через точку![]() параллельно осиOZ
, следовательно, эта прямая целиком
принадлежит поверхности, определяемой
уравнением
параллельно осиOZ
, следовательно, эта прямая целиком
принадлежит поверхности, определяемой
уравнением
![]() ,
и, по определению, эта поверхность -
цилиндрическая с образующей параллельной
осиOZ
.
,
и, по определению, эта поверхность -
цилиндрическая с образующей параллельной
осиOZ
.
Аналогично,
![]() - уравнения цилиндрических поверхностей
с образующими, параллельными соответственно
осямOZ
и OY.
- уравнения цилиндрических поверхностей
с образующими, параллельными соответственно
осямOZ
и OY.
Замечание. На
координатной плоскости XOY
уравнение
![]() определяет линию, которая называется
направляющей рассматриваемой
цилиндрической поверхности.
определяет линию, которая называется
направляющей рассматриваемой
цилиндрической поверхности.
Пример. Уравнение
![]() в пространстве определяет цилиндрическую
поверхность с образующей параллельной
осиOZ
. Направляющей служит окружность радиуса
R
с центром в начале координат, следовательно,
данное уравнение есть уравнение кругового
цилиндра.
в пространстве определяет цилиндрическую
поверхность с образующей параллельной
осиOZ
. Направляющей служит окружность радиуса
R
с центром в начале координат, следовательно,
данное уравнение есть уравнение кругового
цилиндра.
КОНИЧЕСКИЕ ПОВЕРХНОСТИ
Определение.
Поверхность S
называется конической с вершиной в
начале координат O,
если для любой точки
![]() ,
принадлежащейS,
прямая, проходящая через точки O
и
,
принадлежащейS,
прямая, проходящая через точки O
и
![]() ,
целиком лежит на поверхностиS.
,
целиком лежит на поверхностиS.
Уравнение
![]() ,
где
,
где![]() - однородная функция переменных
- однородная функция переменных![]() ,
определяет коническую поверхность с
вершиной в начале координат (
,
определяет коническую поверхность с
вершиной в начале координат (![]() - однородная функция порядкаn,
если для любого t
имеем
- однородная функция порядкаn,
если для любого t
имеем
![]() ,
например,
,
например,![]() - однородная функция второго порядка).
- однородная функция второго порядка).
Пусть точка
![]() принадлежит поверхностиS,
определенной уравнением
принадлежит поверхностиS,
определенной уравнением
![]() ,
где
,
где![]() - однородная функция порядкаn.
Рассмотрим
- однородная функция порядкаn.
Рассмотрим
|
прямую, проходящую
через начало координат O
и точку
Так как радиус-векторы
|
Рис. 29 |
коллинеарны, то
существует число
![]() такое, что
такое, что![]() или
или![]()
Подставим координаты
точки
![]() в левую часть данного уравнения:
в левую часть данного уравнения:![]() (
(![]() ,
так как
,
так как![]() ),
следовательно, любая точка прямой,
проходящей через точкиO
и
),
следовательно, любая точка прямой,
проходящей через точкиO
и
![]() ,
принадлежитS.
Таким образом, уравнение
,
принадлежитS.
Таким образом, уравнение
![]() определяет коническую поверхность.
определяет коническую поверхность.
Пример. Уравнение
![]() есть уравнение конической поверхности,
так как
есть уравнение конической поверхности,
так как![]() - однородная функция второго порядка.
- однородная функция второго порядка.
КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
По аналогии с плоскими линиями устанавливается классификация поверхностей.
Если левая часть уравнения является многочленом степени n, то алгебраическая поверхность называется поверхностью n-го порядка.
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ И ЛИНИЙ
Для определения координат точек пересечения поверхностей, линий или поверхности и линии следует рассматривать совместно уравнения, определяющие рассматриваемые геометрические объекты.
Замечание. Курс аналитической геометрии ограничивается изучением алгебраических линий и поверхностей первого и второго порядка.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Дайте определение уравнение линии на плоскости. Определение параметрических уравнений линии.
Дайте определение уравнения поверхности и уравнений линии в пространстве.
Напишите уравнение цилиндрической поверхности.
Напишите уравнение конической поверхности.
§5. Линейные образы на плоскости
Предположим, что на плоскости задана, декартова прямоугольная система координат. Рассмотрим геометрические объекты на плоскости, определяемые уравнениями первого порядка (линейными уравнениями).
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ
0
Рис. 30.

![]()
![]()
![]()
![]()
![]()
![]() и вектор
и вектор![]() .
Следует записать уравнение прямой,
проходящей через точку
.
Следует записать уравнение прямой,
проходящей через точку![]() перпендикулярно вектору
перпендикулярно вектору![]() (начало вектора
(начало вектора![]() обычно помещают в точку
обычно помещают в точку![]() ,
рис. 30).
,
рис. 30).
Точка
![]() принадлежит прямой тогда и только тогда,
когда
принадлежит прямой тогда и только тогда,
когда![]()
![]() или
или![]() Если
Если![]() и
и![]() - радиус-векторы соответственно точек
- радиус-векторы соответственно точек![]() и
и![]() ,
то
,
то![]() и условие
и условие![]() примет вид
примет вид![]() .
Полученное равенство есть векторное
уравнение прямой, проходящей через
точку
.
Полученное равенство есть векторное
уравнение прямой, проходящей через
точку![]() перпендикулярно вектору
перпендикулярно вектору![]() ;
последний называется нормальным вектором
этой прямой.
;
последний называется нормальным вектором
этой прямой.
O
Рис. 31.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


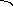

 амечание.
Если начало нормального вектора
амечание.
Если начало нормального вектора![]() поместить в начало координат и при этом
вектор
поместить в начало координат и при этом
вектор![]() будет направлен в сторону прямой (рис.
31), то в произведении
будет направлен в сторону прямой (рис.
31), то в произведении![]() значение
значение![]() равно расстояниюOQ
от начала координат до прямой. Если это
расстояние обозначить через
равно расстояниюOQ
от начала координат до прямой. Если это
расстояние обозначить через
![]() ,
то векторное уравнение прямой
,
то векторное уравнение прямой![]() примет вид
примет вид![]() .
В случае
.
В случае![]() это уравнение имеет вид
это уравнение имеет вид![]() и называется нормированным (нормальным)
уравнением прямой в векторной форме.
и называется нормированным (нормальным)
уравнением прямой в векторной форме.
Векторное уравнение
прямой можно также получить, если задать
точку
![]() и вектор
и вектор![]() ,
параллельно которому проходит прямая
через данную точку (рис. 32). В этом случае
точка
,
параллельно которому проходит прямая
через данную точку (рис. 32). В этом случае
точка![]() принадлежит
принадлежит![]() прямой
тогда и только тогда, когда
прямой
тогда и только тогда, когда![]()
![]() ,
откуда следует, что для любой точки
,
откуда следует, что для любой точки![]() ,
принадлежащей прямой, существует число
,
принадлежащей прямой, существует число![]() такое, что
такое, что![]() или
или![]() .
Полученное уравнение – векторное
уравнение прямой, проходящей через
точку
.
Полученное уравнение – векторное
уравнение прямой, проходящей через
точку![]() в данном направлении.
в данном направлении.
|
Вектор
|
Рис.32 |
ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ
Пусть в заданной
системе координат имеем
![]() ,
тогда
,
тогда![]() и векторное уравнение прямой
и векторное уравнение прямой![]() в координатной форме примет вид
в координатной форме примет вид![]() .
.
Полученное уравнение
называется уравнением прямой, проходящей
через данную точку
![]() ,
перпендикулярно данному направлению,
которое определяется вектором
,
перпендикулярно данному направлению,
которое определяется вектором![]() .
.
Если ввести
обозначение
![]() ,
то получим общее уравнение прямой
,
то получим общее уравнение прямой![]() .
.
НОРМИРОВАННОЕ УРАВНЕНИЕ ПРЯМОЙ
Координатами
единичного вектора являются его
направляющие косинусы, поэтому , если
единичный вектор
![]() ,
то нормированное уравнение прямой
,
то нормированное уравнение прямой![]() в координатной форме будет иметь вид
в координатной форме будет иметь вид![]() .
.
Так как
![]() (рис. 31), то нормированное уравнение
прямой обычно записывают в виде
(рис. 31), то нормированное уравнение
прямой обычно записывают в виде
![]() .
.
Рассмотрим алгоритм
приведение общего уравнения прямой
![]()
![]() к нормированному виду. Нормальный вектор
прямой
к нормированному виду. Нормальный вектор
прямой![]() следует преобразовать в единичный:
следует преобразовать в единичный:
![]() .
.
Для этого обе части
уравнения данной прямой умножим на
![]() :
:
![]() или
или
![]() .
.
В нормированном
уравнении прямой свободный член
![]() ,
где
,
где![]() - расстояние от начала координат до этой
прямой, следовательно, обе части
уравнения, если это необходимо, следует
умножить на (-1). Таким образом, чтобы
общее уравнение прямой привести к
нормированному виду, обе части данного
уравнения следует умножить на
- расстояние от начала координат до этой
прямой, следовательно, обе части
уравнения, если это необходимо, следует
умножить на (-1). Таким образом, чтобы
общее уравнение прямой привести к
нормированному виду, обе части данного
уравнения следует умножить на
![]() ,
,
где знак должен быть противоположным знаку С.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ