8. Кривые линии и кривые поверхности

8.1. Кривые линии

Кривую линию можно рассматривать как след движущейся в пространстве точки или как совокупность точек, удовлетворяющих определенному уравнению. Кривая линия может являться результатом пересечения между собой кривых поверхностей или пересечения кривой поверхности плоскостью.

Если все точки кривой линии лежат в плоскости, то она является плоской, в противном случае - пространственной.

8.2. Плоские кривые линии

Среди плоских кривых выделим кривые, называемыми алгебраическими. Такие кривые линии могут быть заданы алгебраическим уравнением. Степень уравнения определяет порядок кривой линии.

Линии первого порядка - прямые линии.

Кривые линии второго порядка - линии, алгебраическое уравнение которых - уравнение второй степени.

Линии второго порядка - это плоские кривые, определяемые: пятью точками, или четырьмя точками и одной касательной, или тремя точками и двумя касательными, или двумя точками и тремя касательными и т.д. Касательные могут проходить через задаваемые точки.

Линии второго порядка подразделяются на три вида: эллипс, гиперболу и параболу.

ЭЛЛИПС

Эллипс определяется уравнением х²/а² + y²/b² =1

Эллипс имеет две оси симметрии, следовательно и центр.

Наибольший диаметр эллипса - 2а называется большой осью, а малый диаметр - 2b - малой осью. Эти оси взаимно перпендикулярны.

Поскольку эллипс обладает многими геометрическими свойствами, существует множество способов построения его очерков

Рис.8.1

1.Сумма расстояний от любой точки эллипса до двух неподвижных точек, называемых фокусами, есть величина постоянная, равная 2а (рис.8.1).

М₁F₁+M₁F₂=2a

R₁+R₂=2a

AO=A₁O=a; F₁O=F₂O; где:

F₁O= - эксцентриситет эллипса. ВF₁=BF₂=a.

Рис.8.2

2. С помощью двух концентрических окружностей (рис.8.2).

Проводятся две концентрические окружности радиусами ОА и ОВ, а затем из центра О - произвольно выбранные лучи, пересекающие обе окружности в точках 1 и 2 соответственно.

С помощью лучей: 1₁-М₁ и 2₁-М₁ соответственно находят точки М₁ очерка эллипса.

3.по сопряженным диаметрам эллипса (рис.8.3).

Рис.8.3

Если заданы главные оси или два сопряженных диаметра эллипса, то есть такие диаметры, которые делят хорды, соответственно параллельные другому его диаметру пополам, то очерк эллипса можно построить по точкам, указанным на рис.8.3, способом

ГИПЕРБОЛА.

Гипербола определяется уравнением х²/а² - y²/b² =1

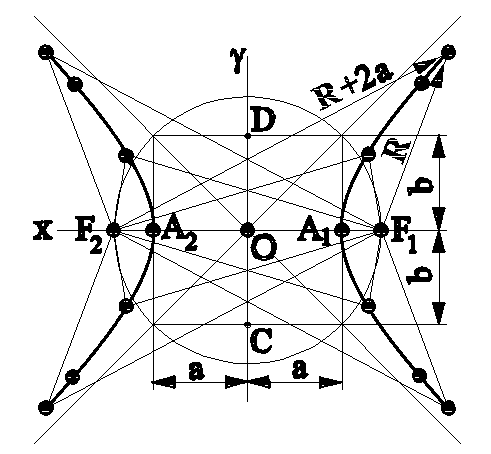
Рис.8.4

Гипербола обладает центром и двумя осями симметрии, имеет две несобственные точки.

Ось симметрии, называемая действительной, пересекает ветви кривой в вершинах А₁ и А₂. Ось, перпендикулярная к действительной оси (и не пересекающую кривую), называют мнимой.

Прямые линии, проходящие через центр и определяющие несобственные точки М_ и N_, называются асимптотами.

При построении гиперболы желательно определить ее центр, диаметр А₁А₂ и асимптоты.

Гипербола, как и эллипс, обладает многими свойствами, на основании которых можно найти множество точек этой кривой.

Гипербола - множество точек плоскости, разность расстояний (радиус-векторов) которых до двух данных точек (фокусов), есть величина постоянная равная 2а - действительной оси гиперболы (рис.8.4). Множество точек гиперболы находят так:

Отмечают точки 1, 2, 3,... на действительной оси гиперболы, постепенно увеличивая расстояния между ними, и проводят из фокуса F₁ дуги радиусами, равными отрезкам А1, А2, А3,..., а из F₂ - отрезками А₁1, А₁2, А₁3,... Пересечение дуг А1 с А₁1, А2 с А₁2, А3 с А₁3,... - точки гиперболы: М₁, М₂, М₃,...

Для построения точек левой ветви кривой из точки F₂ проводят дуги радиусами А1, А2, А3,..., а из F₁ - радиусами А₁1, А₁2, А₁3, ... , но можно использовать осевую или центральную симметрию, как это сделано на чертеже.

2. Построение гиперболы по ее осям, вершинам и точке М. (рис.8.5).

Рис.8.5

Проводят через точку М прямые линии, параллельные осям гиперболы и получают прямоугольник МРА₁Q, а затем диагональ PQ.

Из вершины А проводят произвольный луч, пересекающий МQ в точке 1₁, а из точки 1₁ - прямую, параллельную PQ, получая точку 2₁. Луч А₁2₁ пересечет луч А1 в точке М₁, принадлежащей гиперболе.

Аналогично находятся другие точки гиперболы.

Вторая ветвь гиперболы симметрично найденной.

ПАРАБОЛА.

Парабола определяется уравнением х²=2pz. (y²=2px).

Парабола имеет одну ось симметрии и одну несобственную на ней точку.

Рис.8.6

Парабола - множество точек плоскости, равноудаленных от точки (фокуса) и прямой (директрисы), лежащих в плоскости.

Величина р - расстояние между фокусом и директрисой - параметр параболы. На этом свойстве основано построение параболы по заданным фокусу и директрисе (рис.8.6).

Парабола может быть построена по ее оси, вершине А и точке М одним из двух способов (рис.8.7). Построение точек указано стрелками.

Рис.8.7

Все диаметры параболы параллельны ее оси, так как центр параболы - несобственная точка. Хорды параболы, которые делятся одним из диаметров пополам, называются сопряженными с этим диаметром.

Касательная в конце такого диаметра параллельна сопряженным с ним хордам. (рис.8.8).

Рис.8.8 Рис.8.9

Простой способ проведения касательной к параболе в данной точке дан на рис. 8.9.

ТРАНСЦЕНДЕНТНЫЕ КРИВЫЕ.

Трансцендентными называют кривые линии, заданные, неалгебраическими уравнениями. Например, синусоида. Ее уравнение у=sinx, характеризуют изменение синуса угла в зависимости от величины угла, или циклоида, параметрическое уравнение которой имеет вид: х=r(t – sin(t)), y=r(1+сos(t)).

Более подробно построение кривых линий описано в учебниках по машиностроительному черчению.

Литература.

Левицкий В.С. Машиностроительного черчение: Учебник для студ. втузов - М.:Высш.шк., 1988.

8.3. ПРОСТРАНСТВЕННЫЕ КРИВЫЕ

Пространственные кривые линии - это, главным образом, линии пересечения кривых поверхностей. Так, например, две поверхности второго порядка пересекаются по линии четвертого порядка, представляющей собой пространственную кривую.

8.4. ПРОЕЦИРОВАНИЕ КРИВЫХ ЛИНИЙ

Кривая линия в общем случае проецируется кривой линией (рис.8.10).

Рис.8.10

Алгебраические кривые проецируются кривыми линиями того же порядка, что и сами кривые.

Кривые второго порядка проецируются кривыми линиями второго порядка.

При параллельном проецировании эллипс и окружность проецируются в эллипс или, в частном случае, в окружность; проекция параболы - парабола, проекция гиперболы - гипербола.

При проецировании окружности любая пара ее взаимно перпендикулярных диаметров проецируется парой сопряженных диаметров эллипса.