1,2,3. Расстояния между этим укрупнённым и другими объектами определены по правилу «наиболее удалённого соседа» и представлены в таблице 5.2.5.
Таблица 5.2.5
|
|
1,2,3 |
4,5 |
6 |
|
1,2,3 |
0 |
12,17 |
13,60 |
|
4,5 |
|
0 |
3,61 |
|
6 |
|
|
0 |
Жирным шрифтом в таблице 5.2.5 выделено наименьшее расстояние между объединённым объектом 4,5 и шестым объектами. Их объединяем в
один объект 4,5.6. Расстояния между укрупнёнными объектами определены по правилу «наиболее удалённого соседа» и представлены в таблице 5.2.6.
Таблица 5.2.6
|
|
1,2,3 |
4,5,6 |
|
1,2,3 |
0 |
13.60 |
|
4,5,6 |
|
0 |
Таким образом процесс кластерного анализа закончен . Выделено два кластера. Расстояние между кластерами равно 13,6. Дендрограмма
результатов кластерного анализа представлена на рис. 5.2.2.
14 Расстояние
13,60
12
. . .
. . .
. . .
4
2
1 2 3 4 5 6
Номера объектов
Рис. 5.2.2
Дендрограмма, представленная на рис 5.2.2, отличается от дендрограммы, представленной на рис. 5.1.5. Все остальные результаты примера 5.1 и примера 5.2 одинаковы. Повторим их с изменением номеров таблиц. Представим результаты кластерного анализа в виде совокупности двух матриц: расстояний между объектами (таблица 5.2.7) и символов Кронекера (таблица 5.2.8).
Таблица 5.2.7
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
10,19 |
12,17 |
13,60 |
|
2 |
|
0 |
3,16 |
8,94 |
10,77 |
12,53 |
|
3 |
|
|
0 |
7,07 |
9,06 |
10,44 |
|
4 |
|
|
|
0 |
2,00 |
3,61 |
|
5 |
|
|
|
|
0 |
2,24 |
|
6 |
|
|
|
|
|
0 |
Таблица 5.2.8
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
|
2 |
|
0 |
1,00 |
0,00 |
0,00 |
0,00 |
|
3 |
|
|
0 |
0,00 |
0,00 |
0,00 |
|
4 |
|
|
|
0 |
1,00 |
1,00 |
|
5 |
|
|
|
|
0 |
1,00 |
|
6 |
|
|
|
|
|
0 |
Подсчитаем сумму расстояний между объектами:
0+2,83+3,16+10,19+12,17+13,60+
0+ 0+ 3,16+ 8,94+10,77+12,53+
0+ 0+ 0+ 7,07+ 9,06+10,44+
0+ 0+ 0+ 0+ 2+ 3,61+
0+ 0+ 0+ 0+ 0+ 2,24 =111,77.
Среднее расстояние = 111,77/15=7,45.
Сумма расстояний между объектами, вошедшими в кластеры:
1∙2,83+1∙3,16+1∙3,16+1∙2,00+1∙3,61+1∙2,24=17,00.
Среднее расстояние между объектами в кластерах = 17,00/6=2,83.
Сумма расстояний между объектами, находящимися в разных кластерах:
(1-0)∙10,19+(1-0)∙12,17+(1-0)∙13,60+
+(1-0)∙8,94+(1-0)∙10,77+(1-0)∙12,53+
+(1-0)∙7,07+(1-0)∙9,06+ (1-0)∙10,44= 94,77.
Среднее расстояние между объектами, находящимися в разных кластерах
=94,77/9=10,53.
Таким образом, мы убедились, что условия постановки задачи выполнены, т.е. среднее расстояние между элементами в кластерах более, чем в два с половиной раза меньше чем среднее расстояние между объектами: 7,45/2,83=2,63; а расстояние между объектами, находящимися в различных кластерах почти в полтора раза превышает среднее расстояние между объектами 10,53/7,45=1,41.
Пример 5.3
Евклидово расстояние. По среднему значению
Требуется разделить шесть объектов на два кластера. Объекты –
информационные системы характеризуются двумя признаками:
Х1-среднее время решения одной задачи в минутах;
Х2-количество задач, в решении которых было отказано ввиду перегрузки информационной системы.
Значения признаков Х1 и Х2 для шести объектов представлены в таблице 5.3.1.
Таблица 5.3.1
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
X1 |
2 |
4 |
5 |
12 |
14 |
15 |
|
X2 |
8 |
10 |
7 |
6 |
6 |
4 |
Вычислены расстояния между объектами по формуле Евклида по двум признакам, которые представлены в таблице 5.3.2.
Таблица 5.3.2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
10,19 |
12,17 |
13,60 |
|
2 |
|
0 |
3,16 |
8,94 |
10,77 |
12,53 |
|
3 |
|
|
0 |
7,07 |
9,06 |
10,44 |
|
4 |
|
|
|
0 |
2,00 |
3,61 |
|
5 |
|
|
|
|
0 |
2,24 |
|
6 |
|
|
|
|
|
0 |
Жирным шрифтом в таблице 5.3.2 выделено наименьшее расстояние
между четвёртым и пятым объектами. Их объединяем в один объект 4,5. Расстояния между этим укрупнённым и исходными объектами определены по принципу «среднего значения» и представлены в таблице 5.3.3. Вычисление среднего расстояния пояснено на рис. 5.3.1.
4
3,61
6 m=2,925
2,00
2,24
5
Рис. 5.3.1
Таблица 5.3.3
|
|
1 |
2 |
3 |
4,5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
11,18 |
13,60 |
|
2 |
|
0 |
3,16 |
9,855 |
12,53 |
|
3 |
|
|
0 |
8,065 |
10,44 |
|
4,5 |
|
|
|
0 |
2,925 |
|
6 |
|
|
|
|
0 |
Жирным шрифтом в таблице 5.3.3 выделено наименьшее расстояние
между первым и вторым объектами. Их объединяем в один объект 1,2. Расстояния между этим укрупнённым и остальными объектами определены по принципу « среднего значения» и представлены в таблице 5.3.4.
Таблица 5.3.4
|
|
1,2 |
3 |
4,5 |
6 |
|
1,2 |
0 |
3,16 |
10,5175 |
13,065 |
|
3 |
|
0 |
8,0650 |
10,44 |
|
4,5 |
|
|
0 |
2,925 |
|
6 |
|
|
|
0 |
Жирным шрифтом в таблице 5.3.4 выделено наименьшее расстояние между объектом 4,5 и шестым объектом. Их объединяем в один объект 4,5,6. Расстояния между этим укрупнённым и другими объектами определены по
правилу «среднего значения» и представлены в таблице 5.3.5.
Таблица 5.3.5
|
|
1,2 |
3 |
4,5,6 |
|
1,2 |
0 |
3,16 |
11,79125 |
|
3 |
|
0 |
9,25250 |
|
4,5.6 |
|
|
0 |
Жирным шрифтом в таблице 5.3.5 выделено наименьшее расстояние между объединённым объектом 1,2 и третьим объектом. Их объединяем в
один объект 1,2,3. Расстояния между укрупнёнными объектами определены по правилу «среднего значения» и представлены в таблице 5.3.6.
Таблица 5.3.6
|
|
1,2,3 |
4,5,6 |
|
1,2,3 |
0 |
10,521875 |
|
4,5,6 |
|
0 |
Таким образом процесс кластерного анализа закончен. Выделено два
кластера. Расстояние между выделенными кластерами равно 10,52. Дендрограмма результатов кластерного анализа представлена на рис. 5.3.2.
Расстояние
10,52
10
8
6
4
2
1 2 3 4 5 6
Номера объектов
Рис. 5.3.2
Дендрограмма, представленная на рис 5.3.2, отличается от дендрограммы, представленной на рис. 5.1.5. Все остальные результаты примера 5.1 и примера 5.3 одинаковы. Повторим их с изменением номеров таблиц. Представим результаты кластерного анализа в виде совокупности двух матриц: расстояний между объектами (таблица 5.3.7) и символов Кронекера (таблица 5.3.8).
Таблица 5.3.7
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
10,19 |
12,17 |
13,60 |
|
2 |
|
0 |
3,16 |
8,94 |
10,77 |
12,53 |
|
3 |
|
|
0 |
7,07 |
9,06 |
10,44 |
|
4 |
|
|
|
0 |
2,00 |
3,61 |
|
5 |
|
|
|
|
0 |
2,24 |
|
6 |
|
|
|
|
|
0 |
Таблица 5.3.8
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
|
2 |
|
0 |
1,00 |
0,00 |
0,00 |
0,00 |
|
3 |
|
|
0 |
0,00 |
0,00 |
0,00 |
|
4 |
|
|
|
0 |
1,00 |
1,00 |
|
5 |
|
|
|
|
0 |
1,00 |
|
6 |
|
|
|
|
|
0 |
Подсчитаем сумму расстояний между объектами:
0+2,83+3,16+10,19+12,17+13,60+
0+ 0+ 3,16+ 8,94+10,77+12,53+
0+ 0+ 0+ 7,07+ 9,06+10,44+
0+ 0+ 0+ 0+ 2+ 3,61+
0+ 0+ 0+ 0+ 0+ 2,24 =111,77.
Среднее расстояние = 111,77/15=7,45.
Сумма расстояний между объектами, вошедшими в кластеры:
1∙2,83+1∙3,16+1∙3,16+1∙2,00+1∙3,61+1∙2,24=17,00.
Среднее расстояние между объектами в кластерах = 17,00/6=2,83.
Сумма расстояний между объектами, находящимися в разных кластерах:
(1-0)∙10,19+(1-0)∙12,17+(1-0)∙13,60+
+(1-0)∙8,94+(1-0)∙10,77+(1-0)∙12,53+
+(1-0)∙7,07+(1-0)∙9,06+ (1-0)∙10,44= 94,77.
Среднее расстояние между объектами, находящимися в разных кластерах
=94,77/9=10,53.
Таким образом, мы убедились, что условия постановки задачи выполнены, т.е. среднее расстояние между элементами в кластерах более, чем в два с половиной раза меньше чем среднее расстояние между объектами: 7,45/2,83=2,63; а расстояние между объектами, находящимися в различных кластерах почти в полтора раза превышает среднее расстояние между объектами 10,53/7,45=1,41.
Пример 5.4
Евклидово расстояние. По медиане
Требуется разделить шесть объектов на два кластера. Объекты –
информационные системы характеризуются двумя признаками:
Х1-среднее время решения одной задачи в минутах;
Х2-количество задач, в решении которых было отказано ввиду перегрузки информационной системы.
Значения признаков Х1 и Х2 для шести объектов представлены в таблице 5.4.1.
Таблица 5.4.1
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
X1 |
2 |
4 |
5 |
12 |
14 |
15 |
|
X2 |
8 |
10 |
7 |
6 |
6 |
4 |
Вычислены расстояния между объектами по формуле Евклида по двум признакам, которые представлены в таблице 5.4.2.
Таблица 5.4.2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
10,19 |
12,17 |
13,60 |
|
2 |
|
0 |
3,16 |
8,94 |
10,77 |
12,53 |
|
3 |
|
|
0 |
7,07 |
9,06 |
10,44 |
|
4 |
|
|
|
0 |
2,00 |
3,61 |
|
5 |
|
|
|
|
0 |
2,24 |
|
6 |
|
|
|
|
|
0 |
Жирным шрифтом в таблице 5.4.2 выделено наименьшее расстояние
между четвёртым и пятым объектами. Их объединяем в один объект 4,5. Расстояния между этим укрупнённым и исходными объектами определены по принципу «медианы» и представлены в таблице 5.4.3. Применение принципа по вычислению расстояния между первым объектом и формирующимся объектом, состоящим из 4 и 5 объектов поясняется рис.5.4.1.
4
b=3,61
6
m=2,83
a=2,00
c=2,24
5
Рис.5.4.1
Таблица 5.4.3
|
|
1 |
2 |
3 |
4,5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
7,8692705 |
13,60 |
|
2 |
|
0 |
3,16 |
6,9266965 |
12,53 |
|
3 |
|
|
0 |
5,6583675 |
10,44 |
|
4,5 |
|
|
|
0 |
2,8328 |
|
6 |
|
|
|
|
0 |
Жирным шрифтом в таблице 5.4.3 выделено наименьшее расстояние
между первым и вторым объектами. Их объединяем в один объект 1,2. Расстояния между этим укрупнённым и остальными объектами определены по правилу « медианы» и представлены в таблице 5.4.4.
Таблица 5.4.4
|
|
1,2 |
3 |
4,5 |
6 |
|
1,2 |
0 |
2,8254866 |
7,2767125 |
12.999162 |
|
3 |
|
0 |
5,6583675 |
10,44 |
|
4,5 |
|
|
0 |
2,8328 |
|
6 |
|
|
|
0 |
Жирным шрифтом в таблице 5.4.4 выделено наименьшее расстояние между объектом 1,2 и третьим объектом. Их объединяем в один объект 1,2.3. Расстояния между этим укрупнённым и другими объектами определены по
принципу «медианы» и представлены в таблице 5.4.5.
Таблица 5.4.5
|
|
1,2,3 |
4,5 |
6 |
|
1,2,3 |
0 |
6,363017 |
11,704275 |
|
4,5 |
|
0 |
2,8328 |
|
6 |
|
|
0 |
Жирным шрифтом в таблице 5.4.5 выделено наименьшее расстояние между объединённым объектом 4,5 и шестым объектом. Их объединяем в
один объект 4,5,6. Расстояния между укрупнёнными объектами определены по принципу «медианы» и представлены в таблице 5.4.6.
Таблица 5.4.6
|
|
1,2,3 |
4,5,6 |
|
1,2,3 |
0 |
9,4201385 |
|
4,5,6 |
|
0 |
Таким образом, процесс кластерного анализа закончен. Выделено два
кластера. Расстояние между кластерами равно 9,42. Дендрограмма результа-тов кластерного анализа представлена на рис. 5.4.2
Расстояние
10
9,42
8
6
4
2
1 2 3 4 5 6
Номера объектов
Рис. 5.4.2
Дендрограмма, представленная на рис 5.4.2, отличается от дендрограммы, представленной на рис. 5.1.5. Все остальные результаты примера 5.1 и примера 5.4 одинаковы. Повторим их с изменением номеров таблиц. Представим результаты кластерного анализа в виде совокупности двух матриц: расстояний между объектами (таблица 5.4.7) и символов Кронекера (таблица 5.4.8).
Таблица 5.4.7
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
10,19 |
12,17 |
13,60 |
|
2 |
|
0 |
3,16 |
8,94 |
10,77 |
12,53 |
|
3 |
|
|
0 |
7,07 |
9,06 |
10,44 |
|
4 |
|
|
|
0 |
2,00 |
3,61 |
|
5 |
|
|
|
|
0 |
2,24 |
|
6 |
|
|
|
|
|
0 |
Таблица 5.4.8
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
|
2 |
|
0 |
1,00 |
0,00 |
0,00 |
0,00 |
|
3 |
|
|
0 |
0,00 |
0,00 |
0,00 |
|
4 |
|
|
|
0 |
1,00 |
1,00 |
|
5 |
|
|
|
|
0 |
1,00 |
|
6 |
|
|
|
|
|
0 |
Подсчитаем сумму расстояний между объектами:
0+2,83+3,16+10,19+12,17+13,60+
0+ 0+ 3,16+ 8,94+10,77+12,53+
0+ 0+ 0+ 7,07+ 9,06+10,44+
0+ 0+ 0+ 0+ 2+ 3,61+
0+ 0+ 0+ 0+ 0+ 2,24 =111,77.
Среднее расстояние = 111,77/15=7,45.
Сумма расстояний между объектами, вошедшими в кластеры:
1∙2,83+1∙3,16+1∙3,16+1∙2,00+1∙3,61+1∙2,24=17,00.
Среднее расстояние между объектами в кластерах = 17,00/6=2,83.
Сумма расстояний между объектами, находящимися в разных кластерах:
(1-0)∙10,19+(1-0)∙12,17+(1-0)∙13,60+
+(1-0)∙8,94+(1-0)∙10,77+(1-0)∙12,53+
+(1-0)∙7,07+(1-0)∙9,06+ (1-0)∙10,44= 94,77.
Среднее расстояние между объектами, находящимися в разных кластерах
=94,77/9=10,53.
Таким образом, мы убедились, что условия постановки задачи выполнены, т.е. среднее расстояние между элементами в кластерах более, чем в два с половиной раза меньше чем среднее расстояние между объектами: 7,45/2,83=2,63; а расстояние между объектами, находящимися в различных кластерах почти в полтора раза превышает среднее расстояние между объектами 10,53/7,45=1,41.
Пример 5.5
Евклидово расстояние. По типовым представителям
Требуется разделить шесть объектов на два кластера. Объекты –
информационные системы характеризуются двумя признаками:
Х1-среднее время решения одной задачи в минутах;
Х2-количество задач, в решении которых было отказано ввиду перегрузки информационной системы.
Значения признаков Х1 и Х2 для шести объектов представлены в таблице 5.5.1.
Таблица 5.5.1
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
X1 |
2 |
4 |
5 |
12 |
14 |
15 |
|
X2 |
8 |
10 |
7 |
6 |
6 |
4 |
Вычислены расстояния между объектами по формуле Евклида по двум признакам, которые представлены в таблице 5.5.2.
Таблица 5.5.2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
10,19 |
12,17 |
13,60 |
|
2 |
|
0 |
3,16 |
8,94 |
10,77 |
12,53 |
|
3 |
|
|
0 |
7,07 |
9,06 |
10,44 |
|
4 |
|
|
|
0 |
2,00 |
3,61 |
|
5 |
|
|
|
|
0 |
2,24 |
|
6 |
|
|
|
|
|
0 |
Жирным шрифтом в таблице 5.5.2 выделено наибольшее расстояние
между первым и шестым объектами. Их выбираем в качестве типовых и составим матрицу расстояний между выбранными типовыми и остальными объектами и подсчитаем разницу расстояний каждого объекта от типовых. Результаты вычислений представим в таблице 5.5.3.
Таблица 5.5.3
|
|
1 |
6 |
1-6 |
6-1 |
|
2 |
2,83 |
12,53 |
-9,70 |
9,70 |
|
3 |
3,16 |
10,44 |
-7,28 |
7,28 |
|
4 |
10,19 |
3,61 |
6.51 |
-6,51 |
|
5 |
12,87 |
2,24 |
10,63 |
-10,63 |
Жирным шрифтом в таблице 5.5.3 выделены наименьшие расстояния
между первым и вторым объектами и шестым и пятым объектами. Их объединяем в объекты 1,2 и 5,6. Определим расстояния от укрупнённых объектов до третьего и четвёртого объектов, не вошедших в формируемые кластеры по правилу «ближайшего соседа». Аналогично таблице 5.5.3 составим следующую таблицу 5.5.4.
Таблица 5.5.4
|
|
1,2 |
5,6 |
1,2-5,6 |
5,6-1,2 |
|
3 |
3,16 |
9,06 |
-5,90 |
5,90 |
|
4 |
8,94 |
2,00 |
6,94 |
-6,94 |
По наименьшему расстоянию формируем два кластера 1,2,3 и 4,5,6.Таким образом, процесс кластерного анализа закончен. Выделено два кластера. Дендрограмма результатов кластерного анализа изображена на
рис. 5.5.1.
14 Расстояние
13,60
12
. . .
. . .
. . .
4
2
1 2 3 4 5 6
Номера объектов
Рис. 5.5.1
Дендрограмма, представленная на рис 5.5.1, отличается от дендрограммы, представленной на рис. 5.1.5. Все остальные результаты примера 5.1 и примера 5.5 одинаковы. Повторим их с изменением номеров таблиц. Представим результаты кластерного анализа в виде совокупности двух матриц: расстояний между объектами (таблица 5.5.5) и символов Кронекера (таблица 5.5.6).
Таблица 5.5.5
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
2,83 |
3,16 |
10,19 |
12,17 |
13,60 |
|
2 |
|
0 |
3,16 |
8,94 |
10,77 |
12,53 |
|
3 |
|
|
0 |
7,07 |
9,06 |
10,44 |
|
4 |
|
|
|
0 |
2,00 |
3,61 |
|
5 |
|
|
|
|
0 |
2,24 |
|
6 |
|
|
|
|
|
0 |
Таблица 5.5.6
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
|
2 |
|
0 |
1,00 |
0,00 |
0,00 |
0,00 |
|
3 |
|
|
0 |
0,00 |
0,00 |
0,00 |
|
4 |
|
|
|
0 |
1,00 |
1,00 |
|
5 |
|
|
|
|
0 |
1,00 |
|
6 |
|
|
|
|
|
0 |
Подсчитаем сумму расстояний между объектами:
0+2,83+3,16+10,19+12,17+13,60+
0+ 0+ 3,16+ 8,94+10,77+12,53+
0+ 0+ 0+ 7,07+ 9,06+10,44+
0+ 0+ 0+ 0+ 2+ 3,61+
0+ 0+ 0+ 0+ 0+ 2,24 =111,77.
Среднее расстояние = 111,77/15=7,45.
Сумма расстояний между объектами, вошедшими в кластеры:
1∙2,83+1∙3,16+1∙3,16+1∙2,00+1∙3,61+1∙2,24=17,00.
Среднее расстояние между объектами в кластерах = 17,00/6=2,83.
Сумма расстояний между объектами, находящимися в разных кластерах:
(1-0)∙10,19+(1-0)∙12,17+(1-0)∙13,60+
+(1-0)∙8,94+(1-0)∙10,77+(1-0)∙12,53+
+(1-0)∙7,07+(1-0)∙9,06+ (1-0)∙10,44= 94,77.
Среднее расстояние между объектами, находящимися в разных кластерах
=94,77/9=10,53.
Таким образом, мы убедились, что условия постановки задачи выполнены, т.е. среднее расстояние между элементами в кластерах более, чем в два с половиной раза меньше чем среднее расстояние между объектами: 7,45/2,83=2,63; а расстояние между объектами, находящимися в различных кластерах почти в полтора раза превышает среднее расстояние между объектами 10,53/7,45=1,41.
Пример 5.6
Расстояние Хемминга. Ближайший сосед
Требуется разделить шесть объектов на два кластера. Объекты –
информационные системы характеризуются двумя признаками:
Х1-среднее время решения одной задачи в минутах;
Х2-количество задач, в решении которых было отказано ввиду перегрузки информационной системы.
Значения признаков Х1 и Х2 для шести объектов представлены в таблице 5.6.1.
Таблица 5.6.1
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
X1 |
2 |
4 |
5 |
12 |
14 |
15 |
|
X2 |
8 |
10 |
7 |
6 |
6 |
4 |
Вычислены расстояния между объектами по формуле Хемминга по двум признакам. Проведение вычислений для второго и пятого объектов пояснено рис.5.6.1 и для второго и шестого объектов рис 5.6.2. Результаты вычислений расстояний по Хеммингу представлены в таблице 5.6.2.
10
Х2
8 1
6
5
4
d15
=|2-14|+|8-6|=14
2
2 4 6 8 10 12 14 Х1
Рис.5.6.1
10
Х2
2
8
6
4
6
2
d26
=|4-15|+|10-4|=17
2 4 6 8 10 12 14 Х1
Рис.5.6.2
Таблица 5.6.2
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
4 |
4 |
12 |
14 |
17 |
|
2 |
|
0 |
4 |
12 |
14 |
17 |
|
3 |
|
|
0 |
8 |
10 |
13 |
|
4 |
|
|
|
0 |
2,00 |
5 |
|
5 |
|
|
|
|
0 |
3 |
|
6 |
|
|
|
|
|
0 |
Жирным шрифтом в таблице 5.6.2 выделено наименьшее расстояние между четвёртым и пятым объектами. Их объединяем в один объект 4,5. Расстояния между этим укрупнённым и исходными объектами определены
по правилу «ближайшего соседа» и представлены в таблице 5.6.3.
Таблица 5.6.3
-
1
2
3
4,5
6
1
0
4
4
12
17
2
0
4
12
17
3
0
8
13
4,5
0
3
6
0
Далее процесс выделения объектов в кластеры производится аналогично ранее рассмотренным методам. По таблице 5.6.3 находим минимальное расстояние между объектом, включающим в себя 4 и 5 объекты, и 6 объектом, которые объединяем в объект 4,5,6 и составляем таблицу 5.6.4.
Таблица 5.6.4
|
|
1 |
2 |
3 |
4,5,6 |
|
1 |
0 |
4 |
4 |
12 |
|
2 |
|
0 |
4 |
12 |
|
3 |
|
|
0 |
8 |
|
4,5,6 |
|
|
|
0 |
Ввиду того, что расстояния между 1,2 и 3 объектами одинаковые и минимальные, то вначале объединяем 1 и 2 объекты и результаты такого объединения помещаем в таблицу 5.6.5. Затем к ним присоединяем 3 объект и результаты объединения помещаем в таблицу 5.6.7.
Таблица 5.6.6
|
|
1,2 |
3 |
4,5,6 |
|
1,2 |
0 |
4 |
12 |
|
3 |
|
0 |
8 |
|
4,5,6 |
|
|
0 |
Таблица 5.6.7
-
1,2,3
4,5,6
1,2,3
0
8
4,5,6
0
На рис.5.6.3 представлена дендрограмма результатов кластерного анализа.
Расстояние
8
8,00
6
4
2
1 2 3 4 5 6
Номера объектов
Рис.5.6.3
Представим результаты кластерного анализа в виде совокупности двух матриц: расстояний между объектами (таблица 5.6.8) и символов Кронекера (таблица 5.6.9).
Таблица 5.6.8
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
4 |
4 |
12 |
14 |
17 |
|
2 |
|
0 |
4 |
12 |
14 |
17 |
|
3 |
|
|
0 |
8 |
10 |
13 |
|
4 |
|
|
|
0 |
2,00 |
5 |
|
5 |
|
|
|
|
0 |
3 |
|
6 |
|
|
|
|
|
0 |
Таблица 5.6.9
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0 |
1,00 |
1,00 |
0,00 |
0,00 |
0,00 |
|
2 |
|
0 |
1,00 |
0,00 |
0,00 |
0,00 |
|
3 |
|
|
0 |
0,00 |
0,00 |
0,00 |
|
4 |
|
|
|
0 |
1,00 |
1,00 |
|
5 |
|
|
|
|
0 |
1,00 |
|
6 |
|
|
|
|
|
0 |
Подсчитаем сумму расстояний между объектами:
0+
4+ 4+ 12+ 14+ 17+
0+ 0+ 4+ 12+ 14+ 17+
0+ 0+ 0+ 8+ 10+ 13+
0+ 0+ 0+ 0+ 2+ 5+
0+ 0+ 0+ 0+ 0+ 3 =139.
Среднее расстояние = 139/15=9,27.
Сумма расстояний между объектами, вошедшими в кластеры:
1∙4+1∙4+1∙4+1∙2+1∙5+1∙3=22.
Среднее расстояние между объектами в кластерах = 22/6=3,67.
Сумма расстояний между объектами, находящимися в разных кластерах:
(1-0)∙12+(1-0)∙14+(1-0)∙17+
+(1-0)∙12+(1-0)∙14+(1-0)∙17+
+(1-0)∙8+(1-0)∙10+(1-0)∙13= 117.
Среднее расстояние между объектами, находящимися в разных кластерах
=117/9=13.
Таким образом, мы убедились, что условия постановки задачи выполнены, т.е. среднее расстояние между элементами в кластерах более, чем в два с половиной раза меньше чем среднее расстояние между объектами: 9,27/3,67=2,52; а расстояние между объектами, находящимися в различных кластерах почти в полтора раза превышает среднее расстояние между объектами 13/9,27=1,4.
Рассмотренные шесть примеров наглядно продемонстрировли методику применения основных методов кластерного анализа. Получение одинаковых результатов по всем рассмотренным методам объясняется сравнительной несложностью рассматриваемого примера. При усложнении примера следует ожидать различий в результатах кластерного анализа.
Задание 1.6
Пример 6.1
Провести сглаживание и временное прогнозирование количества персональных компьютеров в организациях РФ в тысячах методом скользящего среднего с шагом m=3 числа. Первые пять значений использовать для прогнозирования; три последних значения использовать для оценки качества аппроксимации и спрогнозировать ещё три значения на 2011, 2012 и 2013 годы.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
Вычислим сглаженные значения числа ПК:
Вычислим цепной годовой прирост:
Вычислим спрогнозированные значения числа ПК для оценки качества:
Вычислим среднее значение для трёх спрогнозированных лет:
Вычислим среднеквадратическую ошибку прогнозирования:
Вычислим отношение ошибки к среднему значению:
Так как отношение среднеквадратической ошибки к среднему значению превышает рекомендуемое значение 0.05 сравнительно на немного, то резуль-тат признаем допустимым.
Полученные результаты сглаживания и прогнозирования.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
|
Число ПК: сглаженное, спрогнозир. |
4026.6 |
4806.1 |
5650.6 |
6640.7 |
7485.1 |
7436.6 |
8032.0 |
8495.7 |
Спрогнозируем количество ПК в 2011, 2012, 2013 годах.
Вычислим спрогнозированные значения числа ПК для оценки качества:
Полученные результаты сглаживания и прогнозирования.
|
Год |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Число ПК |
8267,3 |
8743,7 |
9288,1 |
- |
- |
- |
|
Число ПК: спрогнозированное |
7436.6 |
8032.0 |
8495.7 |
8832.6 |
9297.9 |
9719.9 |
На рис.6.1 результаты сглаживания и прогнозирования представлены в графическом виде.
у
11
10
9
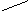
Экспериментальные
значения
8
Спрогнозированные
значения
7
6
Сглаженные
значения
5
4
3
4 5 6 7 8 9 10 11
12 13 х 
Рис.6.1
Пример 6.2
Провести сглаживание и временное прогнозирование количества персональных компьютеров в организациях РФ в тысячах методом взвешенного скользящего среднего с шагом m=3 числа. Первые пять значений использовать для прогнозирования; три последних значения использовать для оценки качества аппроксимации и спрогнозировать ещё три значения на 2011, 2012 и 2013 годы.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
Вычислим сглаженные значения числа ПК:
Вычислим цепной годовой прирост:
Вычислим
спрогнозированные значения числа ПК
для оценки качества:
Вычислим среднее значение для трёх спрогнозированных лет:
Вычислим среднеквадратическую ошибку прогнозирования:
Вычислим отношение ошибки к среднему значению:
Так как отношение среднеквадратической ошибки к среднему значению меньше рекомендуемого значения 0.05 примерно в два раза, то результат прогнозирования признаем удовлетворительным.
Полученные результаты сглаживания и прогнозирования.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
|
Число ПК: сглаженное, спрогнозир. |
4026.6 |
4806.1 |
5585.7 |
6713.5 |
7550.1 |
8302,3 |
9020,1 |
9729,6 |
Спрогнозируем количество ПК в 2011, 2012, 2013 годах.
Вычислим спрогнозированные значения числа ПК для оценки качества:
Полученные результаты сглаживания и прогнозирования.
|
Год |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Число ПК |
8267,3 |
8743,7 |
9288,1 |
- |
- |
- |
|
Число ПК: спрогнозированное |
8302,3 |
9020,1 |
9729,6 |
10434,7 |
11139,2 |
11843,0 |
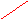
На рис.6.2 результаты
сглаживания и прогнозирования представлены
в графическом виде.
у
12
11
10
9
Экспериментальные
значения Спрогнозированные
значения
8
7
6
Сглаженные
значения
5
4
3
4 5 6 7 8 9 10 11
12 13 х
Рис.6.2
Пример 6.3
Провести сглаживание и временное прогнозирование количества персональных компьютеров в организациях РФ в тысячах экспоненциальным методом с α=0,3. Первые пять значений использовать для прогнозирования; три последних значения использовать для оценки качества аппроксимации и спрогнозировать ещё три значения на 2011, 2012 и 2013 годы.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
Вычислим сглаженные значения числа ПК:
Вычислим цепной годовой прирост:
Вычислим спрогнозированные значения числа ПК для оценки качества:
Вычислим среднее значение для трёх спрогнозированных лет:
Вычислим среднеквадратическую ошибку прогнозирования:
Вычислим отношение ошибки к среднему значению:
Так как отношение среднеквадратической ошибки к среднему значению превышает рекомендуемое значение 0.05 более чем в четыре раза результат признаем неудовлетворительным.
Полученные результаты сглаживания и прогнозирования.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
|
Число ПК: сглаженное, спрогнозир. |
4150,5 |
4272,8 |
4703,9 |
5298.0 |
5967,1 |
5752,0 |
6155,9 |
6126,5 |
Спрогнозируем
количество ПК в 2011, 2012, 2013 годах.
Полученные результаты прогнозирования.
|
Год |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Число ПК |
8267,3 |
8743,7 |
9288,1 |
- |
- |
- |
|
Число ПК: спрогнозированное |
5752,0 |
6155,9 |
6126,5 |
6400,4 |
6462,0 |
6672,2 |
На рис.6.3 результаты сглаживания и прогнозирования представлены в графическом виде.
у
11
10
9
Экспериментальные
значения
8
Спрогнозированные
значения
7
6
5
Сглаженные
значения
4
3
4 5 6 7 8 9 10 11
12 13 х 
Рис.6.3
Пример 6.4
Провести сглаживание и временное прогнозирование количества персональных компьютеров в организациях РФ в тысячах экспоненциальным методом с α=0,9. Первые пять значений использовать для прогнозирования; три последних значения использовать для оценки качества аппроксимации и спрогнозировать ещё три значения на 2011, 2012 и 2013 годы.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
Вычислим сглаженные значения числа ПК:
Вычислим цепной годовой прирост:
Вычислим спрогнозированные значения числа ПК для оценки качества:
Вычислим среднее значение для трёх спрогнозированных лет:
Вычислим среднеквадратическую ошибку прогнозирования:
Вычислим отношение ошибки к среднему значению:
Так как отношение среднеквадратической ошибки к среднему значению меньше рекомендуемого значения 0.05 более чем в четыре раза, то результат признаем вполне приемлемым.
Полученные результаты сглаживания и прогнозирования.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
|
Число ПК: сглаженное, спрогнозир. |
4150,5 |
4517,5 |
5590,4 |
6574,6 |
7433,0 |
8107.2 |
8799.8 |
9490.6 |
Спрогнозируем количество ПК в 2011, 2012, 2013 годах.
Полученные результаты прогнозирования.
|
Год |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Число ПК |
8267,3 |
8743,7 |
9288,1 |
- |
- |
- |
|
Число ПК: спрогнозированное |
8107.2 |
8799.8 |
9490.6 |
10181.5 |
10872.5 |
11563.4 |
На рис.6.4 результаты сглаживания и прогнозирования представлены в графическом виде.
у
12
11
Спрогнозированные
значения
10
9
Экспериментальные
значения
8
7
6
Сглаженные
значения
5
4
3
4 5 6 7 8 9 10 11
12 13 х
Рис.6.4
Пример 6.5
Провести сглаживание и временное прогнозирование количества персональных компьютеров в организациях РФ в тысячах методом наименьших квадратов с линейной функцией у=b0+b1·x. Первые пять значений использовать для прогнозирования; три последних значения использовать для оценки качества аппроксимации и спрогнозировать ещё три значения на 2011, 2012 и 2013 годы.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
х |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Число ПК=у |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
Вычислим вспомогательные переменные:
Вычислим коэффициенты аппроксимирующего уравнения регрессии:
Таким образом получили аппроксимирующее уравнение:
y=1285.41+888.15·x.
Вычислим сглаженные значения числа ПК:
Вычислим спрогнозированные значения числа ПК для оценки качества:
Вычислим среднее значение для трёх спрогнозированных лет:
Вычислим среднеквадратическую ошибку прогнозирования:
Вычислим отношение ошибки к среднему значению:
Так как отношение среднеквадратической ошибки к среднему значению меньше рекомендуемого значения 0.05, то результат признаем удовлетвори-тельным.
Полученные результаты сглаживания и прогнозирования.
|
Год |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
Число ПК |
4150,5 |
4558,3 |
5709,6 |
6684,0 |
7528,4 |
8267,3 |
8743,7 |
9288,1 |
|
Число ПК: сглаженное, спрогнозир. |
3949.9 |
4838.0 |
5726.2 |
6614.3 |
7502.5 |
8390.6 |
9278.8 |
10166.9 |
Спрогнозируем количество ПК в 2011, 2012, 2013 годах.
Вычислим спрогнозированные значения числа ПК для оценки качества:
|
Год |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
|
Число ПК |
8267,3 |
8743,7 |
9288,1 |
- |
- |
- |
|
Число ПК: спрогнозированное |
8390.6 |
9278.8 |
10166.9 |
11055.1 |
11943.2 |
12831.4 |
Р
езультаты
сглаживания и прогнозирования в
графическом виде представлены на рис.
6.5.
у
13
12
11
Спрогнозированные значения у=1285+888·х
10
9
Экспериментальные
значения
8
7
6
Сглаженные
значения
5
4
3
4 5 6 7 8 9 10 11
12 13 х
Рис.6.5