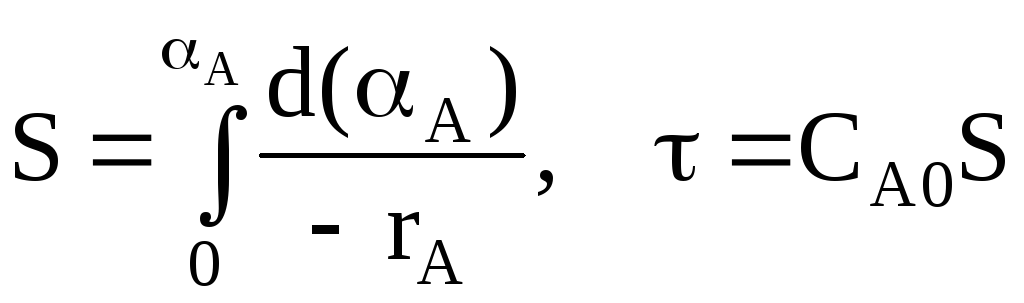Материальный баланс реактора

Материальный баланс – это равенство прихода и расхода вещества в реакторе или в процессе. Теоретической основой составления материальных балансов является закон сохранения материи М.И. Ломоносова.

Составим материальный баланс реактора, в котором протекает простая необратимая реакция А → С.

Масса реагента, поступающего в реактор, в единицу времени, равно массе реагента А, расходуемому в реакторе в единицу времени.

m_{А приход} = m_{Арасход}

Реагент А расходуется на химическую реакцию, часть реагента выходит из реактора, часть – остается в реакционном объеме в неизменном виде (накапливается).

m_{Арасход} = m_{А хим.р.} + m_{А сток} + m_{А накопл.}

m_{А приход} = m_{А хим.р.} + m_{А сток} + m_{А накопл.}

m_{А приход} - m_{А сток} = m_{А хим.р.} + m_{А накопл.}

Обозначим m_{А приход}-m_{А сток}=m_{А конвек.}– масса реагента А, переносимого за счет конвекции (потоком реакционной массы).

Тогда m_{А накопл.}=m_{А конвек.}-m_{А хим.р.}

Масса реагента А, остающееся неизменным в реакционном потоке, равно разнице между массой вещества А, переносимым конвективным потоком, и массой вещества А, израсходованным на химическую реакцию. Это есть уравнение материального баланса в общем виде.

Когда концентрация реагента непостоянна в различных точках объема реактора или во времени, нельзя составлять материальный баланс в общем виде, для всего объема реактора. В этом случае составляют материальный баланс для элементарного объема реактора.

Основой этого материального баланса является уравнение конвективного переноса (см. Амелин и др. с.71-73).

где С_А – концентрация реагента А в реакционной смеси;

x,y,z – пространственные координаты;

W_x, W_y, W_z – составляющие скорости потока;

D – коэффициент диффузии;

r_A – скорость химической реакции.

Член характеризует изменение концентрации реагента А во времени в элементарном объеме и соответствуетm_{А накопл.} в общем уравнении материального баланса.

Член отражает изменение концентрации реагента вследствие переноса его в направлении, совпадающим с направлением общего потока.

Член отражает изменение концентрации реагента А в элементарном объеме в результате переноса его путем диффузии. Вместе эти члены характеризуют суммарный перенос вещества в движущейся среде путем конвекции и диффузии; в общем уравнение материального баланса им соответствует членm_{А конвек.}.

Член r_A показывает изменение концентрации реагента А в элементарном объеме за счет химической реакции. Ему соответствует член m _{А хим.р.} в общем уравнении материального баланса.

Полученное дифференциальное уравнение очень сложно в решении. В зависимости от типа реактора и режима его работы оно может быть преобразовано и упрощено.

Лекция № 12 Гидродинамические модели реакторов. Вывод характеристических уравнений.

Ранее мы рассмотрели основные модели химических процессов и их математическое описание. Усложним модель химико-технологического процесса за счет учета гидродинамических процессов, то есть способов направленного движения потоков реакционной смеси в реакторе.

Любой реактор, используемый в химическом производстве. В большем или меньшем приближении можно описать одной из следующих моделей:

• реактор идеального смешения периодического действия РИС-П;

• реактор идеального смешения непрерывного действия РИС-Н;

• реактор идеального вытеснения непрерывного действия РИВ-Н;

• каскад реакторов идеального смешения непрерывного действия К-РИВ-Н (ячеечная модель).

Для каждой модели выведено характеристическое уравнение, которое выражает зависимость времени пребывания реагентов в реакторе о, начальной концентрации реагента, величины конверсии и скорости химической реакции.

τ = f (C_A0, α_A, r_A)

Это уравнение является математическим описанием модели реактора. Оно дает возможность, задав С_А0 (состав исходной смеси) и r_A (тип химической реакции, температуру, давление, катализатор и т.п.) рассчитать время пребывания реагентов в реакторе, необходимое для достижения заданной конверсии (α_A), а значит, и объем реактора, его габаритные размеры и производительность. Сравнивая полученные значения для реакторов разного типа, можно выбрать самый оптимальный вариант для проведения данной химической реакции.

Основанием для вывода характеристического уравнения является материальный баланс реактора, составленный по одному их компонентов реакционной смеси.

Реактор идеального смешения периодического действия

РИС-П представляет собой аппарат с мешалкой, в который периодически загружают исходные реагенты и также периодически выгружают продукты.

В таком реакторе создается такое интенсивное перемешивание, что в каждый момент времени концентрация реагентов одинакова по всему объему реактора и изменяется лишь во времени, по мере протекания химической реакции.

Исходным уравнением для получения характеристического уравнения является уравнение материального баланса в дифференциальной форме:

Так как вследствие интенсивного перемешивания все параметры одинаковы по всему объему реактора, в любой момент времени производная любого порядка от концентрации по осям x,y,z равна нулю.

Тогда

При V_{реакци.смеси} = const C_A = C_A0 (1-α_А).

- характеристическое уравнение РИС-П

Если в реакторе протекает простая необратимая реакция «n»-го порядка, то

При n = 0 ,

n = 1 .

При n ≠ 0 и 1 определение τ производят методом графического интегрирования. Для этого строят графическую зависимость

вычисляют площадь под кривой между начальным и конечным значением степени превращения.