ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ СИСТЕМЫ ТЕЛ

С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА.

Цель работы – определить момент инерции системы четырех одинаковых грузов массы m двумя способами: 1) экспериментально с помощью маятника Обербека, 2) теоретически, считая грузы материальными точками. Сравнить полученные результаты.

Приборы и принадлежности: маятник Обербека, секундомер, масштабная линейка, набор грузов, штангенциркуль.

Теоретическое введение

Момент инерции – физическая величина, характеризующая инертность тела при вращательном движении.

Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат ее расстояния до оси (см. рис. 1)

Моментом инерции произвольного тела относительно оси называется сумма моментов инерции материальных точек из которых состоит тело, относительно этой оси (см. рис. 2)

Для однородных тел правильной геометрической формы можно заменить суммирование интегрированием.

,

где dm = ρdV (ρ – плотность вещества, dV– элемент объема)

Таким образом получены формулы некоторых тел массой m относительно оси, проходящей через центр тяжести:

а) стержня длиной относительно оси, перпендикулярной стержню

,

б) обруча (а также тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча и проходящей через его центр тяжести (совпадающей с осью цилиндра)

,

где – радиус обруча (цилиндра)

в) диска (сплошного цилиндра) относительно оси, перпендикулярной плоскости диска и проходящей через его центр тяжести (совпадающей с осью цилиндра )

,

где – радиус диска (цилиндра)

г) шара радиуса R относительно оси произвольного направления, проходящей через его центр тяжести

^.

Момент инерции тела зависит: 1) от формы и размеров тела, 2) от массы и распределения масс, 3) от положения оси относительно тела.

Теорема Штейнера о параллельных осях записывается как:

,

где – момент инерции тела массой m относительно произвольной оси, – момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно произвольной оси, – расстояние между осями.

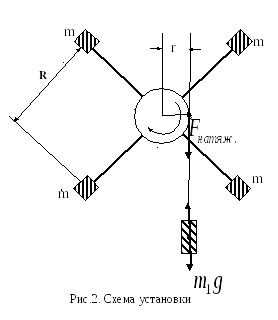
Описание установки.

Маятник Обербека представляет собой крестовину, состоящую из шкива и четырех равноплечих стержней, закрепленных на горизонтальной оси (см. рис.2). На стержнях на равных расстояниях от оси вращения насажены четыре одинаковых груза массы m каждый. При помощи груза m₁, прикрепленного к концу шнура, намотанного на один из шкивов, вся система может быть приведена во вращательное движение. Для отсчета высоты падения h груза m₁ имеется вертикальная шкала.

Запишем второй закон Ньютона для падающего груза в векторной форме

(1)

где - сила тяжести; - сила натяжения шнура (см. рис. 1);

- линейное ускорение, с которым падает груз m₁ вниз.

Принимая направление движения груза за положительное, перепишем уравнение (I) в скалярной форме

(2)

откуда получим выражение для силы натяжения шнура

(3)

Линейное ускорение a находится из формулы пути равноускоренного движения без начальной скорости

(4)

где h – высота падения груза m₁; t – время падения.

Сила натяжения нити F_нат вызывает ускоренное вращение крестовины. Основной закон вращательного движения крестовины с учетом сил трения запишется так :

M – M_тр = I i , (5)

где М – момент силы натяжения; M_тр - момент сил трения; I - момент инерции крестовины; i - угловое ускорение, с которым вращается крестовина. Величина момента сил трения M_тр по сравнению с величиной вращающего момента М невелика, и, следовательно, ею можно пренебречь.

Из уравнения ( 5 ) с учетом сделанного замечания получаем оконча-тельную формулу для расчета момента инерции крестовины

(6)

где r - радиус шкива. Угловое ускорение i определяется по формуле

(7)

Подставляя (3) и (7) в (6), получаем окончательную формулу для расчета момента инерции крестовины

(8)

Порядок выполнения работы.

Часть I.

Экспериментальное определение момента инерции системы 4^х грузов.

1. Снять со стержней грузы m .

2. Намотать в один слой шнур на шкив, установив груз m₁ на заранее выбран-ной высоте h. Отпустив крестовину, замерить время падения t_о груза с помо-щью секундомера. Опыт повторить пять раз (при одной и той же высоте паде-ния h ).

3. Закрепить на концах стержней грузы m.

4. Выполнить операции, указанные в пункте 2, измеряя секундомером время падения t. Опыт повторить пять раз.

5. С помощью штангенциркуля измерить диаметр шкива d в пяти разных положениях.

6. Результаты измерений занести в таблицу. Найти приближенные значения и по методу Стьюдента оценить абсолютные погрешности измерения величин t_о, t и d.

7. По формуле (4) рассчитать величину линейного ускорения a, с которым падает груз m₁ для случаев:

а) крестовина без грузов (a_о),

б) крестовина с грузами (а).

8. По формуле (8) вычислить момент инерции крестовины без грузов (I_o) и с грузами (I), используя приближенные значения m_{1, R,} g и полученные значения а и а_о.

1. Вычислить погрешности измерений по формулам:

(9)

(10)

Таблица 1

Результаты измерений и вычислений

№ п/п	to, c	t, c	d, м	h, м	m = (0,144+0,005) кг m1 = (0,175+ 0,005) кг R = (0,220 + 0,003) м
1 2 3 4 5
Приближен. значения
Абсолютная погрешность

Часть II.

1. Теоретически найти момент инерции системы 4^х грузов массы m, находящихся на расстоянии R от оси вращения (считая грузы материальными точками)

(11)

2. Сравнить результаты эксперимента и расчетов. Вычисть относительную погрешность

(12)

и сделать вывод о том, как велико расхождение полученных результатов.

Контрольные вопросы.

1. Что называется моментом инерции материальной точки и произвольного тела?

2. От чего зависит момент инерции тела относительно оси вращения?

3. Приведите примеры формул момента инерции тел. Как они получены?

4. Теорема Штейнера о параллельных осях и ее практическое использование.

5. Вывод формулы для расчета момента инерции крестовины с грузами и без грузов.

Литература

1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.

2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.

3. Зисман Г. А., Тодес О. М.. Курс общей физики для втузов: в 3 т. Т. 1: Механика, молекулярная физика, колебания и волны - 4-е изд., стереотип. - М.: Наука, 1974. - 340 с.

4. Методические указания к выполнению лабораторных работ по разделу “Механика“.- Иваново, ИХТИ, 1989 г. (под редакцией Биргера Б.Н.).