Расчет надёжности

Государственное образовательное учреждение высшего профессионального образования

«Ивановский государственный Химико-технологический университет»

Кафедра информационных технологий

Расчёт надёжности информационной системы

Выполнила:

ст-ка гр.3-42

Жехрова Ю.А

Проверила:

Чаусова С.М

Вариант №7

Иваново 2009

Задание:

По структурной схеме надежности информационной системы и заданным значениям интенсивности отказов ее элементов:

1) построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0,1 – 0,2;

2) определить время наработки системы соответствующее заданному γ (гамма-процентному ресурсу системы);

3) обеспечить при заданном γ (гамма-процентном ресурсе) увеличение времени наработки системы не менее чем в 1,5 раза за счет структурного резервирования элементов системы.

Все элементы системы работают в режиме нормальной эксплуатации. Резервирование отдельных элементов или групп элементов должно осуществляться идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.

Структурная схема надежности:

Рис.1

Значения интенсивности отказов элементов составляют:

Расчет

1. В исходной схеме элементы 2,6,9 и 11 соединены последовательно. Заменяем их элементом A, для которого:

2. Элементы 3,7 и 10 также образуют последовательное соединение, заменив которое элементом В, получим:

3. Элементы 4 и 8 также образуют последовательное соединение, заменив которое элементом С, получим:

4. Элементы 12 и 13 образуют параллельное соединение. Заменяем их элементом D, для которого при p₁₂ = p₁₃ , получим:

Преобразованная схема будет иметь вид:

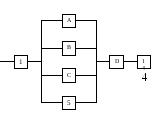
Рис.2

5. Элементы A,B,C и 5 образуют параллельное соединение. Заменив их элементом Е, получим:

P_E=1-(1-P_A)*(1-P_B)*(1-P_C)*(1-P₅)

После преобразования схема примет вид:

Рис.3

Элементы 1 и E образуют последовательное соединение, заменив которое элементом H, получим:

Рис.4

6. В преобразованной схеме элементы H, D и 14 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы определяется выражением:

7. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 14 подчиняются экспоненциальному закону:

8. Результаты расчетов вероятностей безотказной работы элементов 1 – 14 исходной схемы по предыдущей формуле представлены в таблице.

Таблица 1

		Наработка, t – 1 000 000 ч
Элемент		0,5	1	1,5	2	2,5	3	3,5	1,56	2,34
1	0,05	0,9753	0,9512	0,9277	0,9048	0,8825	0,8607	0,8395	0,9250	0,8896
2 – 5	0,5	0,7788	0,6065	0,4724	0,3679	0,2865	0,2231	0,1738	0,4584	0,3104
6-8	0,05	0,9753	0,9512	0,9277	0,9048	0,8825	0,8607	0,8395	0,9250	0,8896
9,10	0,005	0,9975	0,995	0,9925	0,9900	0,9876	0,9851	0,9827	0,9922	0,9884
11	0,1	0,9512	0,9048	0,8607	0,8187	0,7788	0,7408	0,7047	0,8556	0,7914
12,13	0,2	0,9048	0,8187	0,7408	0,6703	0,6065	0,5488	0,4966	0,7320	0,6263
14	0,1	0,9512	0,9048	0,8607	0,8187	0,7788	0,7408	0,7047	0,8556	0,7914
А	-	0,7207	0,5194	0,3744	0,2698	0,1945	0,1402	0,1010	0,3599	0,2160
B	-	0,7577	0,5741	0,4350	0,3296	0,2497	0,1892	0,1433	0,4207	0,2729
C	-	0,7596	0,5769	0,4382	0,3329	0,2528	0,1920	0,1459	0,4240	0,2761
D	-	0,9909	0,9671	0,9328	0,8913	0,8452	0,7964	0,7466	0,9282	0,8603
E	-	0,9964	0,9659	0,8952	0,7936	0,6778	0,5624	0,4565	0,8843	0,7154
H	-	0,9718	0,9188	0,8305	0,7180	0,5982	0,4841	0,3832	0,8180	0,6364
P	-	0,9160	0,8041	0,6668	0,5240	0,3937	0,2856	0,2016	0,6496	0,4333
H’	-	1,0000	1,0000	0,9992	0,9937	0,9739	0,9291	0,8553	0,9989	0,9825
P’	-	0,9426	0,8751	0,8022	0,7251	0,6411	0,5482	0,4500	0,7932	0,6689

8. Результаты расчетов вероятностей безотказной работы квазиэлементов А, В, С, D, Е, Н по формулам также представлены в таблице.

10. На рисунке представлен график зависимости вероятности безотказной работы системы Р от времени (наработки) t.

Рис.5

11. По графику (кривая Р) находим для γ = 65% (Р = 0.65) γ-процентную наработку системы t = 1,56·10⁶ ч.

12. Проверочный расчет при t = 1,56·10⁶ ч. показывает (Таблица 1), что P_γ = 0,6496 ~ 0,65.

13. По условиям задания находим время, превышающее в 1,5 раза время, соответствующее вероятности безотказной работы, равной 0,65 (P_γ = 0,65):

= 1,5·1,56·10⁶ = 2,34·10⁶ ч.

14. Расчет показывает (Таблица 1), что при = 2,34·10⁶ ч. для элементов преобразованной схемы p_H () =0,6364; p_D ()=0,8603; p₁₄ ()= 0,7914. Следовательно, из трёх последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент H, и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.

15. Для того чтобы при = 2,34  10⁶ ч система в целом имела вероятность безотказной работы P’ = 0,65, надо найти необходимую вероятность безотказной работы элемента H. Так как

,

где – необходимая вероятность безотказной работы элемента H, то

16. Для элемента H системы резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов достаточно сложно, так как число элементов должно быть целым.

17. Для повышения надежности системы добавляем к ней элементы, идентичные по надежности элементу Н, до тех пор, пока вероятность безотказной работы квазиэлемента Н’ не достигнет заданного значения:

-добавляем элемент J, получаем:

Рис.6

P_H^’=1-(1-P_H)*(1-P_J) =1-(1-0,6364)*(1-0,6364) =0,8678<0,9547

- добавляем элемент I, получаем:

Рис.7

P_H^’=1-(1-P_H)*(1-P_J) *(1-P_I) =1-(1-0,6364)*(1-0,6364) *(1-0,6364) =0,9519<0,9547

-добавляем элемент K, получаем:

Рис.8

P_H^’=1-(1-P_H)*(1-P_J) *(1-P_I) *(1-P_K) =1-(1-0,6364)*(1-0,6364) *(1-0,6364) *(1-0,6364) =0,9825>0,9547.

18. Таким образом, для повышения надежности до требуемого уровня, необходимо в схеме (Рис.4) систему достроить элементами J, I и K до конечной системы (Рис.8).

19. Результаты расчетов вероятностей безотказной работы квазиэлемента «H’» и системы в целом Р’ представлены в таблице.

20. Расчеты показывают, что при t’ = 2,3410⁶ ч, Р’ =0,6689>0,65, что соответствует условию задания.

ВЫВОДЫ:

1. По данным расчета вероятности безотказной работы системы от времени построен график P(t).

2. По графику найдено время, соответствующее 65% γ -процентному ресурсу системы (t = 1,56  10⁶ ч).

3. Для увеличения наработки системы в 1,5 раза при 65% γ -процентном ресурсе системы предложено нагруженное резервирование элемента Н, идентичными по надежности резервными элементами J, I и K.

4. Рассчитана вероятность безотказной работы системы с повышенной надежностью от времени, построен график P’(t) системы с повышенной надежностью, на графике (Рис.5) показано время (t’ = 2,34  10⁶ ч) соответствующее 65% γ -процентному ресурсу.