1.8. Расчет цепей методом контурных токов.

Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.

Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений.

П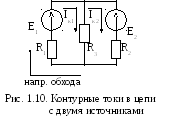 ри расчете рекомендуется придерживаться следующей последовательности:

– выделить все независимые контуры

– указать направления обхода контуров (желательно одно и то же для всех контуров)

– указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода)

– для всех независимых контуров составить уравнения второго закона Кирхгофа

– решить полученную систему уравнений любым известным методом

– по вычисленным значениям контурных токов определить величины токов в ветвях и их направления.

Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E₁R₃R₁E₁ и R₃E₂R₂R₃. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R₃, которая принадлежит двум контурам сразу, протекают два контурных тока I_K1 и I_K2, но в противоположных направлениях.

E ₁ = I_K1 (R₁ + R₃) – I_K2R₃

– E₂ = – I_K1 R₃ + I_K2 (R₂+ R₃)

Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление.

Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: I_K1 =7 A, I_K2 = – 5 A. Тогда I₁ = I_K1 = 7 = 7 A и протекает в резисторе R₁ так же, как контурный ток I_K1 по схеме сверху вниз. Ток I₂ = – I_K2 = – 5 А и протекает в резисторе R₂ по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R₃ , цепи представленной на рис. 1.10, протекают контурный ток I_K1 = 7 А по схеме сверху вниз и контурный ток I₂ = – 5 А по схеме снизу вверх. I_K1 > I_K2 и I₃ = I_K1 – I_K2 = 7 – (–5) = 12 А. Ток I₃ имеет такое же направление, что и ток I_K1 , т.е. по схеме сверху вниз.

1.9. Расчет цепей методом эквивалентного преобразования.

Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений.

По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента.

Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в)

Например, в цепи представленной на рис. 1.11а приемники R₃ и R₄ соединены последовательно и их можно заменить одним эквивалентным с сопротивлением

R₃₄ = R₃ + R₄.

После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R₂ и эквивалентный приемник R₃₄ включены параллельно. Параллельный участок R₂ – R₃₄ также можно заменить одним эквивалентным с сопротивлением

после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно.

Входное сопротивление этой цепи R₁₂₃₄ = R₁ + R₂₃₄

позволяет найти ток I₁ исходной цепи рис. 1.11а, пользуясь законом Ома

.

Напряжение на участке R₂₃₄ легко найти по закону Ома для пассивного участка цепи

U₂₃₄ = I₁R₂₃₄.

Токи в ветвях R₂ и R₃₄ также находятся по закону Ома

.

Токи I₃ = I₄, т.к. приемники R₃ и R₄ включены последовательно, они равны току I₃₄.