2.10. Резонанс в последовательной цепи элементов r-l-c.

Режим работы, при котором цепь, несмотря на наличие в ней реактивных элементов, ведет себя как идеальная активная, называется резонансом.

Как показано в предыдущем разделе, в этом случае реактивные сопротивления равны, т.е.

X_L= X_C,

а угол сдвига фаз между током и напряжением

= 0

Так как , а, то частота, при которой наступит резонанс, определяется формулой:

.

(2.64)

Формула 2.64 показывает, что при неизменных параметрах элементов цепи ее можно ввести в резонанс, изменяя частоту, а при неизменной частоте - изменяя параметры.

В режиме резонанса активная мощность

,

т.к. соs= 1 , а ток в цепи определяется только активным сопротивлением R, т.к. X_L= X_C

,

(2.65)

т.е. ток и активная мощность достигают максимальных значений, и вся энергия источника необратимо преобразуется в другой вид.

Однако, несмотря на это режим резонанса, который в данном случае называется резонансом напряжений, следует рассматривать как аварийный, особенно при наличии больших реактивных сопротивлений, включенных в цепь. В этом случае напряжения на реактивных элементах окажутся в раз больше, чем на зажимах цепи, что может привести к пробою изоляции реактивных элементов и выходу их из строя.

2.11. Параллельная цепь элементов r-l-c при синусоидальном токе.

Пусть к цепи рис. 2.19 подведено синусоидальное напряжение

u= U_msin,

или в комплексной форме

На основании первого закона Кирхгофа комплекс тока в неразветвленной части цепи равен сумме комплексов токов в ветвях, т.е.

I=I_R+I_L+I_C, (2.66)

а на основании закона Ома комплексы токов в ветвях

.

Подставляя комплексы токов в ветвях цепи в 2.66, получим

,

(2.67)

= g называется активной проводимостью;

= b_L – реактивной индуктивной проводимостью;

=b_C– реактивной емкостной проводимостью цепи.

Подставив значения проводимостей в 2.67 получим:

,

(2.68)

Y= g – j( b_L– b_C) называется комплексом полной проводимости цепи; запишем ее в показательной форме

.

(2.69)

Модуль комплекса полной проводимости

,

(2.70)

аргумент комплекса полной проводимости

.

(2.71)

Подставляя комплексы напряжения и полной проводимости в 2.68 получим

,	(2.72)

т.е. вектор тока в неразветвленной части цепи сдвинут относительно вектора напряжения на угол , величина которого определяется параметрами цепи.

Если b_L– b_C> 0, то < 0 и ток отстает от напряжения на угол

i=I_msin(),

цепь в этом случае носит индуктивный характер;

если b_L– b_C< 0, то > 0, а ток опережает напряжение на угол

i=I_msin(),

цепь в этом случае носит емкостный характер;

если b_L= b_C, то = 0 и ток совпадает по фазе с напряжением

i=I_msin,

а цепь носит активный характер.

Из 2.72 следует, что

.

(2.73)

Выражение 2.73 есть закон Ома для действующих значений напряжения и тока.

В соответствии со значениями комплексов напряжения и токов в ветвях на рис. 2.20 построена векторная диаграмма для случая индуктивной цепи, т.е когда b_L> b_C.

Выделенный на диаграмме треугольник называется треугольником токов, из рассмотрения которого следуют формулы, широко используемые в практических расчетах:

, (2.74)

. (2.75)

Разность между индуктивным током I_Lи емкостным током I_Cназывается реактивным током и обозначается I_P.

Поделив все стороны треугольника токов на напряжение, получим треугольник проводимостей (рис. 2.21), из которого следует полученная ранее формула модуля комплекса полной проводимости

а также формулы активной и реактивной проводимостей

.

(2.76)

П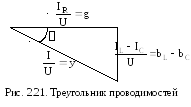оскольку законы изменения токов и напряжений и их фазовые соотношения в последовательной и параллельной цепях одинаковы, то естественно, что идентичными будут и энергетические процессы, протекающие в них. Формулы для расчета мощностей в параллельной цепи будут такими же, что и для расчета в последовательной цепи.