
- •Численные методы (Методические указания и задания)
- •Численное интегрирование
- •1. 1. Метод прямоугольников
- •1. 2. Метод трапеций
- •1. 3. Метод парабол (метод Симпсона)
- •Приближенное решение алгебраических и трансцендентных уравнений
- •2. 1. Уточнение корней методом половинного деления
- •2. 2. Метод итераций
- •2. 3. Метод хорд
- •2. 4. Метод касательных (Метод Ньютона)
- •2. 5. Комбинированный метод хорд и касательных
- •Аппроксимация функций
- •3. 1. Математическая постановка задачи интерполирования
- •3. 2. Интерполяционный многочлен Лагранжа
- •3. 3. Линейная интерполяция
- •3. 4. Метод наименьших квадратов
- •3. 5. Нахождение параметров линейной функции
- •3. 6. Нахождение параметров квадратичной функции
- •Решение систем линейных уравнений
- •Содержание
501
Численные методы (Методические указания и задания)
Составители С.И. Смуров
В.А. Таланова
С.П. Бобков
Иваново 2003
В методических указаниях рассматриваются методы приближенного вычисления определенного интеграла, численного решения алгебраических и трансцендентных уравнений, вопросы математической обработки экспериментальных данных.
Даны примеры решения задач и задания для самостоятельной работы.
Указания составлены в соответствии с программой и одобрены решением цикловой методической комиссией по физико-математическим дисциплинам.
Численное интегрирование
Вычислить
определенный интеграл
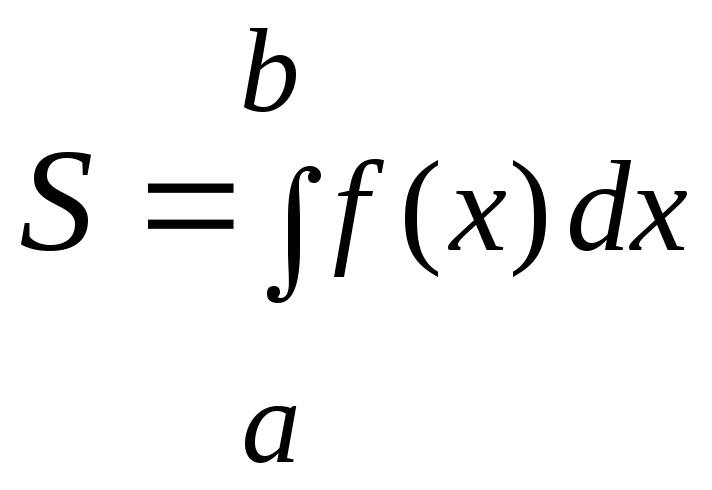 ,
где
,
где![]() – непрерывная функцияx
в интервале
– непрерывная функцияx
в интервале
![]() ,
можно с помощью аналитической формулы,
если использовать прием формального
интегрирования по формуле Ньютона-Лейбница
(I.
I.)
,
можно с помощью аналитической формулы,
если использовать прием формального
интегрирования по формуле Ньютона-Лейбница
(I.
I.)
 ,
(I.
I.)
,
(I.
I.)
где
![]() – первообразная функция для заданной
функции
– первообразная функция для заданной
функции![]() .
.
Однако во многих
случаях не удается найти никакой
аналитической формулы в виду невозможности
определения
![]() .
.
В таких случаях приходится применять методы численного интегрирования.
Основной принцип
построения всех приближенных формул
численного интегрирования состоит в
том, что интервал интегрирования
разбивается на множество меньших
отрезков, внутри которых подынтегральная
кривая
![]() заменяется с некоторой степенью точности
более простыми функциями, интегралы от
которых можно вычислить, используя
ординаты на концах отрезков.
заменяется с некоторой степенью точности
более простыми функциями, интегралы от
которых можно вычислить, используя
ординаты на концах отрезков.
1. 1. Метод прямоугольников
Вычисление интеграла
 равносильно вычислению площади некоторой
фигуры – криволинейной трапеции с
параллельными «основаниями»x=a,
x=b
и «боковыми сторонами» y=0,
y=f(x),
рис. I.
I.
равносильно вычислению площади некоторой
фигуры – криволинейной трапеции с
параллельными «основаниями»x=a,
x=b
и «боковыми сторонами» y=0,
y=f(x),
рис. I.
I.
y y=f(x)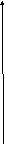
y2








y1

y0
yn-1

h h h h




x
a
x1
x2
x3
xn-1 b
Рис. 1. 1.
Разобьем интервал интегрирования на n равных частей, каждая длиной h=(b-a)/n.
Приближенное значение интеграла получается в виде сумм площадей n прямоугольников, высота которых равна значению f(x) на левом краю каждого подинтервала, т.е. формула численного интегрирования имеет вид (I. 2.):
 или
или
 (I.
2.)
(I.
2.)
и называется формулой «левых» прямоугольников.
Если в качестве приближенного значения площади для каждого подинтервала принять площадь прямоугольника, высота которого равна значению f(x) на правом краю подинтервала, то формула численного интегрирования будет иметь вид (I. 3.):
 (I.
3.)
(I.
3.)
и называется формулой «правых» прямоугольников.
1. 2. Метод трапеций
В соответствии с полученными ранее формулами «левых» и «правых» прямоугольников истинное значение интеграла лежит между приближенными значениями, определяемыми по этим формулам (рис. I. 2), т.е. лучшую формулу численного интегрирования можно получить, взяв среднее арифметическое этих значений:
y y=f(x)
yi+1




yi


h

x
xi
xi+1
Рис. 1. 2


 .
(I.
4)
.
(I.
4)
Эта формула (I.
4) описывает метод трапеций для численного
интегрирования, т.е. приближенное
значение интеграла
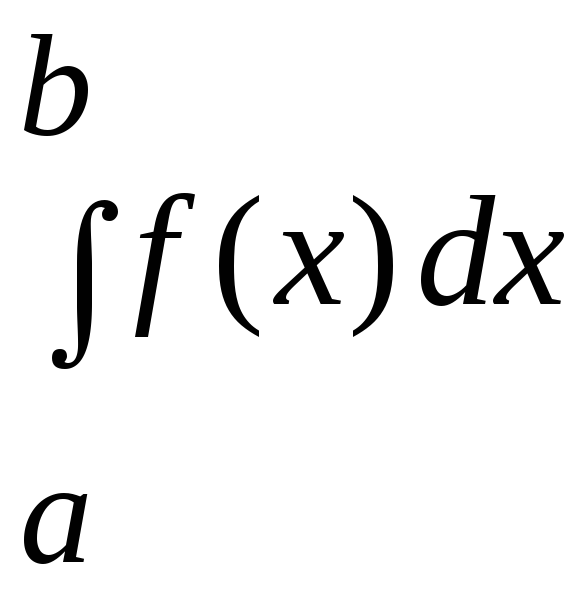 получается в виде суммы площадей «n»
трапеций.
получается в виде суммы площадей «n»
трапеций.
