
книги / Теория механизмов и машин курсовое проектирование
..pdf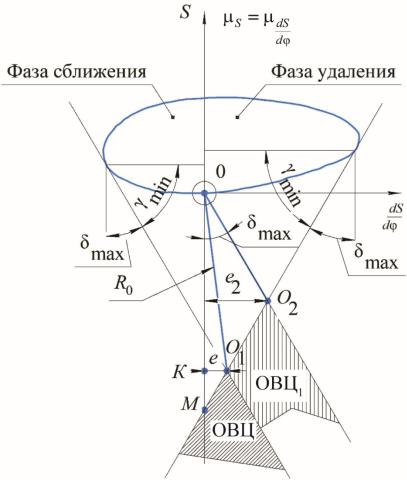
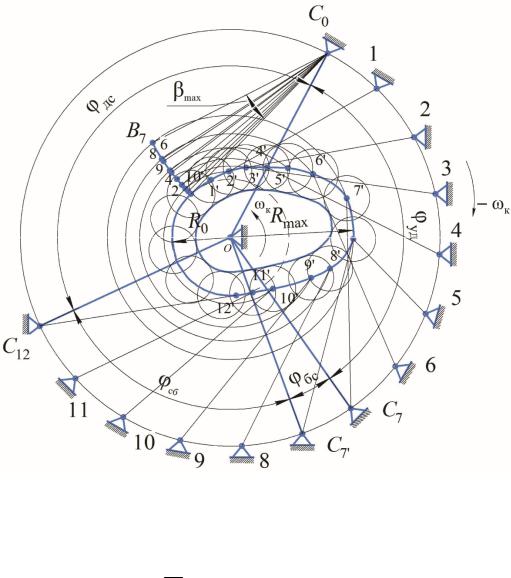
Рис. 4.1. Определение R0 и е для различных областей возможных центров вращения кулачка (ОВЦ – область двустороннего вращения; ОВЦ1 – область одностороннего вращения)
3. При геометрическом замыкании высшей кинематической пары к кривой совмещенного графика слева и справа проводятся две касательные
подуглом δmax квертикальной оси0S илиподугломγmin коси ddSφ. Точка О1 –
пересечение касательных (см. рис. 4.1), ограничивающих область возможных центров вращения кулачка (область ОВЦ заштрихована на рис. 4.1).
Минимальное значение начального радиуса R0 = (0O1)μS; e = (O1K)μS. Любая точка области ОВЦ может быть принята за центр вра-
щения кулачка.
Острый угол между прямой из центра вращения кулачка и любой точкой совмещенного графика с вертикалью, проведенной через эту точку, дает угол давления меньше δmax, а угол передачи движения больше γmin
(рис. 4.1).
Кулачковый механизм со смещением имеет меньший R0, чем центральный механизм (см. рис. 4.1). Отрезок МO = R0 для центрального
80
кулачкового механизма. Габариты кулачкового механизма со смещением в данном случае будут меньше.
Замечание
При силовом замыкании в высшей кинематической паре, когда кулачок одностороннего вращения, допускается некоторое увеличение угла δ (уменьшение угла γ).
В этом случае проводится касательная под углом max ( min) только к кривой S = f ddSφ на фазе удаления. Из точки 0 под углом δmax к вертикали
(γmin – к горизонтали) проводится прямая до пересечения в точке О2 с ран-
нее проведенной касательной (см. рис. 4.1). Центр вращения кулачка можновыбратьвточкеО2,чтопозволитуменьшитьначальный(минимальный) радиус и габариты кулачкового механизма: R0 = μS (0O2).
При этом выбор точки О2 или точек в зоне ОВЦ1 позволяет выдерживать на фазе удаления условия < max ( > min).
R0 вслучае силовогозамыканияменьше,чемпригеометрическомзамыкании. Смещение е толкателя увеличивается. Выбор R0 по различным условиям иллюстрируется в рис. 4.1. В ряде случаев величиной эксцентриситета е задаются.
4.1.1. Построение профиля кулачка
Первоначально проводят построение центрового профиля кулачка, выбрав масштабный коэффициент μS и переводя известные геометрические
параметры R0 и е в отрезки чертежа. Порядок дальнейших построений:
1.Из произвольной точки O проводят окружности радиусов R0 и е
(рис. 4.2).
2.К окружности эксцентриситета проводят касательную, соответствующую оси движения толкателя (с учетом расположения эксцентриситета).
3.От точки В0 пересечения этой касательной и начальной окружности (нижнее положение толкателя) откладывают текущие перемещения Si конца толкателя на фазах удаления и сближения в соответствии с диаграммой S = f(φ) в масштабе μS.
4.Затем соединяют наиболее удаленную точку оси перемещений с центром вращения кулачка О и этим радиусом проводят окружность, на которой откладывают фазовые углы. Началом отсчета для фазовых углов служит радиус OВ7. В соответствии с методом обращенного движения отсчетугловведетсяпротивдвижениякулачка(нарис.4.2 кулачоквращается против часовой стрелки).
81
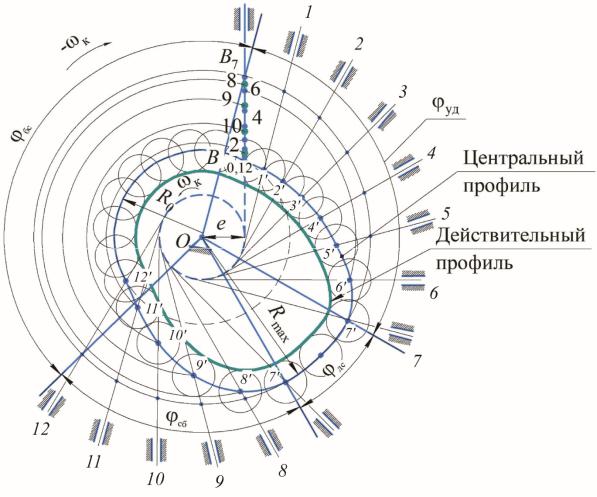
Рис. 4.2. Профилирование кулачка
5. Через точки деления фазовых углов проводят касательные к окружности эксцентриситета е (необходимо учитывать знак смещения е).
Из центра вращения кулачка О проводят дуги OВ1, OВ2 и т.д. до пересечения с соответствующими касательными. Точки пересечения 1', 2', 3' являютсяточкамицентрового(теоретического)профилякулачка(см.рис.4.2).
4.1.2. Определение размеров ролика толкателя
Для повышения надежности, уменьшения износа и потерь на трение в высшей кинематической паре на толкателе устанавливают ролик.
Радиус ролика выбирается из двух соображений:
rр ≤ 0,4R0 , rр ≤ 0,7÷0,8 ρmin
где min минимальный радиус кривизны центрового профиля.
Первое условие (4.1) конструктивности обеспечивает одинаковую контактную прочность для звеньев, образующих высшую кинематическую
82
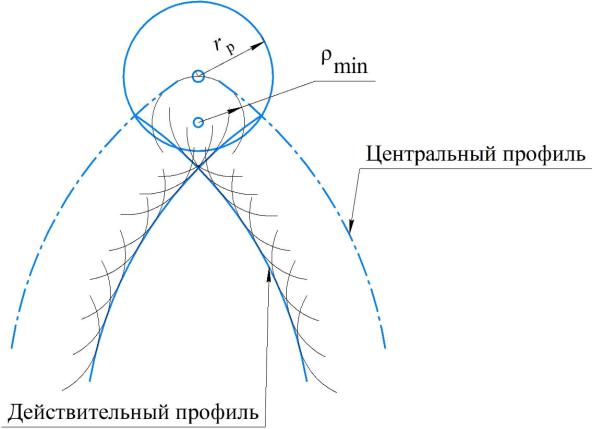
пару.Нарушениеэтогоусловияможетпривестикослаблениювалакулачка
(рис. 4.3).
При выполнении второго условия (4.1) действительный профиль кулачканезаостряетсяинесамопересекается.Этоспособствуетвыполнению заданного закона движения, который в противном случае нарушается за счет заострения и самопересечения профиля, а работа механизма сопровождается значительным износом звеньев (см. рис. 4.3).
Рис. 4.3. К обоснованию выбора радиуса ролика
Минимальный радиус кривизны ρmin на центровом (теоретическом)
профиле находят, проводя окружности через три точки. Эти точки располагают по возможности на близком расстоянии друг от друга в том месте теоретического профиля, где кривизна максимальна, а радиус кривизны минимален (см. рис. 4.3).
Наряду с условиями(4.1) следует учесть, что увеличение rр приводит к увеличению массы толкателя, ухудшая его динамические характеристики. Уменьшение rр увеличивает габариты кулачка и его массу.
Огибающая дуг окружностей радиуса rр, имеющих центр на центровом (теоретическом) профиле, – действительный профиль (см. рис. 4.2).
83

4.2.Определение основных размеров кулачка
сроликовым коромыслом
Известны:закондвижениякулачкаикоромысла;максимальныйугол давления δmax (минимальный угол передачи движения γmin); фазовые углы,
длина коромысла lк, м, и максимальный угол качания коромысла βmax.
Следует определить начальный радиус R0 и межцентровое расстояние aw между центрами вращения кулачка и коромысла.
Алгоритм решения задачи.
1. Строятдиаграммыперемещения,первойивторойпроизводныхперемещения конца коромысла по углу поворота кулачка.
При этом текущее перемещение конца коромысла в i-м положении Si = lкβi, где Si дуговое перемещение конца коромысла в метрах при его отклонении на угол βi, рад.
2. Изображают совмещенный график, соблюдая условия равенства масштабных коэффициентов μS = μdS.
dφ
Если указанные масштабные коэффициенты на соответствующих диаграммах разные, то при их уравнивании ординаты соответствующих графиков следует преобразовать по рассмотренным ранее методикам.
Из произвольной точки С (рис. 4.4) радиусом, равным B0C= lк , про-
μS
водят дугу В0В. От точки В0 по дуге В0В с графика перемещения откладывают соответствующие отрезки Si = Lк βi, где Lк=μlкS. Текущие точки 0, 1, 2,
… , 24 (см. рис. 4.4) соответствуют положению центра ролика коромысла при заданных углах поворота кулачка.
3. На лучах СВ0, CВ1, CВ2 и т.д. откладывают отрезки dS/dφ . При
μS
этом следует придерживаться следующего правила: при вращении кулачка
икоромыславодномнаправлениинафазеудаленияотрезки dS/dφ откла-
μS
дываются по соответствующим лучам от дуги В0В в направлении С, а от-
резки dS/dφ на фазе сближения – в сторону, противоположную точке С.
μS
При вращении кулачка и коромысла в противоположных направлениях
(см. рис. 4.4) отрезки dS/dφ на фазе удаления откладываются от дуги В0В
μS
в сторону, противоположную центру С вращения коромысла, а на фазе
сближения отрезки dS/dφ – в сторону точки С.
μS
84
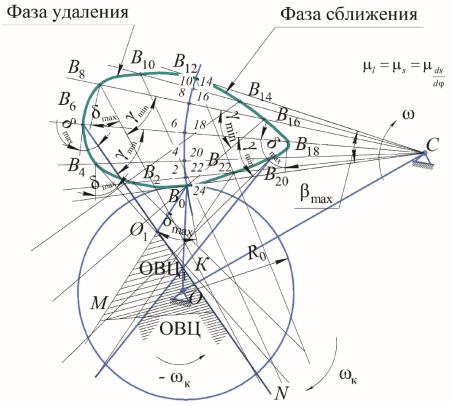
4. Через полученные точки Вi совмещенного графика проводят прямые под углом δmax к перпендикулярам лучей CBi в этих точках (или проводят прямые под углом γmin к соответствующим лучам). Область, ограни-
ченнаяэтимипрямыми(нарис.4.4 оназаштрихована),рассматриваетсякак область возможных центров вращения кулачка. Для любой точки этой области выполняется условие, что в процессе работы кулачкового механизма угол давления δ на всех фазах движения не будет больше δmax (угол передачи γ на всех фазах не будет меньше γmin).
Выбрав за центр вращения кулачка, например, точку O, получают, что OВ0 дает величину R0 = ОВ0 μS, причем R0min = KВ0 μS. Межцентровое расстояние aw = OC μS (aw = KC μS) в случае выбора точки К за центр вра-
щения кулачка.
При проектировании кулачка одностороннего вращения в случае силового замыкания δ ≤ δmax (γ ≥ γmin) выполняется только на фазе удаления.
Поэтому из точки В0 проводят луч под углом δmax к перпендикуляру отрезка СВ0 на фазе сближения.
Область центров вращения кулачка может быть принята в виде области ОВЦ1, а точка О1 – за центр вращения кулачка, тогда R0 min = O1B0 μS, aw = O1C μS. Используя условие одностороннего вращения кулачка, можно
уменьшить габариты кулачкового механизма.
Рис. 4.4. Определение начального радиуса R0 для кулачкового механизма с коромыслом
85
4.2.1. Построение профиля кулачка
Определив начальный радиус R0 и межцентровое расстояние aw, строят центровой профиль кулачка.
1. Выбирают масштабный коэффициент μl. Из центра О проводят
окружность радиусом |
aw = OC , мм, соответствующим межосевому рас- |
|
0 |
|
μl |
стоянию.
2. По методу обращенного движения от произвольной точки С0 этой окружности, противоположно вращению кулачка откладывают фазовые углы, деля их на то же число равных частей в соответствии с диаграммой перемещения. Получают точки С1, С2 и т.д. (рис. 4.5).
Рис. 4.5. Профилирование кулачка с коромыслом
3. Из точки О радиусом |
R0 |
мм проводят начальную окружность. |
|
μ |
|
|
l |
|
4.Радиусом BC lк , мм, соответствующим длине коромысла из
l
точки C0 проводят дугу В0В7. На дуге В0В7 откладывают текущие положения конца коромысла согласно диаграмме перемещения (см. рис. 4.5).
86
5.ИзцентраO проводятокружностирадиусовОВi черезсоответствующие точки деления дуги В0В7, а из точек С1, С2 и т.д. радиусом ВC делают засечки на соответствующих окружностях.
Врезультате пересечения этих дуг получают точки центрового (теоретического) профиля кулачка (см. рис. 4.5).
6.Радиусроликавыбираетсявсоответствиисметодикойп.4.1.2. Как
ив п.4.1.2, строится действительный профиль кулачка, как огибающая положения ролика (см. рис. 4.5).
График изменения угла давления δ (угла передачи движения γ) по углу поворота кулачка представлен на рис. 4.6. При графическом определении угла δ (γ) все точки В1,В2 и т.д. совмещенного графика (см. рис. 4.4) соединяют с центром вращения кулачка O. Тогда острые углы, образованные этими прямыми с перпендикулярами в точках Вi к соответствующим лучам, являются углами давления δi, а острые углы между прямыми ОВi и
лучами СВi определяют углы передачи γi.
Рис. 4.6. График изменения величины угла давления
Профилирование кулачка представлено на рис.4.5, а пример изменения угла давления изображен на рис. 4.6.
4.3Определение минимальных размеров кулачка
споступательно движущимся плоским толкателем
Вкулачковых механизмах с поступательно движущимся плоским толкателем угол давления (передачи) постоянен во время работы механизма. Наилучшая силовая работоспособность такого механизма достигаетсяприугледавленияδ = 0 (γ = 90°),когдаплоскостьтолкателяперпендикулярна его оси движения.
Плоскость толкателя должна последовательно контактировать со всемиточкамипрофилякулачка.Этоприводиткусловиювыпуклостипрофиля. Тогда радиус кривизны профиля кулачка больше нуля, т.е. ρ > 0.
87
4.3.1. Метод профессора Я.Л. Геронимуса
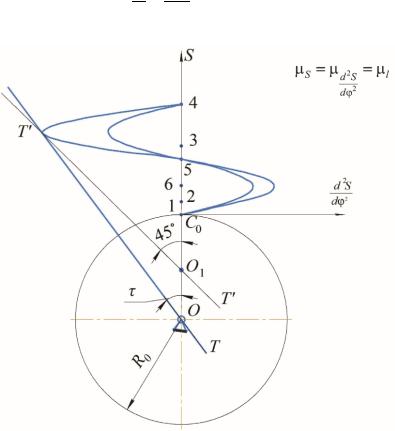
Радиус кривизны определяется через геометрические и кинематические параметры кулачкового механизма:
|
– ddφ22S |
i |
|
– ddφ22S |
|
|
|
|||||||
|
|
|
|
< 1 или |
|
|
i |
< tg45° |
(4.2) |
|||||
|
R |
0 |
+ S |
|
R |
0 |
+ S |
|||||||
|
|
|
|
i |
|
i |
|
|
|
|||||
В силу этого по диаграммам S = S(φ) и |
d2S |
= |
d2S |
(φ) строится совме- |
||||||||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dφ |
|
dφ |
|
|
2 |
|
|
(рис. 4.7). При построении масштабные коэф- |
||||||||||
щенный график S = f d |
|
S2 |
||||||||||||
dφ |
|
|
|
|
|
|
|
|
|
|
|
|||
фициенты μS и μd2S должны быть равными. Если при построении закона
dφ2
движениятолкателяонибылиразными,тоихследуетвыровнятьссоответственным изменением ординат диаграмм. Причем, если μS или μd2S больше
dφ2
масштабного коэффициента совмещенного графика l, то ординаты S и d2S
dφ2
μd2S
увеличиваются в μS и dφ2 раз и наоборот.
μl μl
|
В части совме- |
||||
|
щенной |
диаграммы |
|||
|
(рис. |
4.7), соответ- |
|||
|
ствующей |
макси- |
|||
|
мальным по модулю |
||||
|
отрицательным |
зна- |
|||
|
чениям |
d2S |
, проводят |
||
|
2 |
||||
|
|
dφ |
|
|
|
|
касательную T |
– T |
|||
|
под углом |
45° к оси |
|||
|
ОS. |
|
|
|
|
|
На основе усло- |
||||
|
вия (4.2) центр враще- |
||||
|
ния О кулачка распо- |
||||
|
лагается |
ниже |
точки |
||
|
O1. Таким |
образом, |
|||
|
|
|
|
например, |
|
Рис. 4.7. Совмещенный график |
R0 = (OC0) μl. |
|
|||
88
4.3.2. Метод суммирования ординат графиков
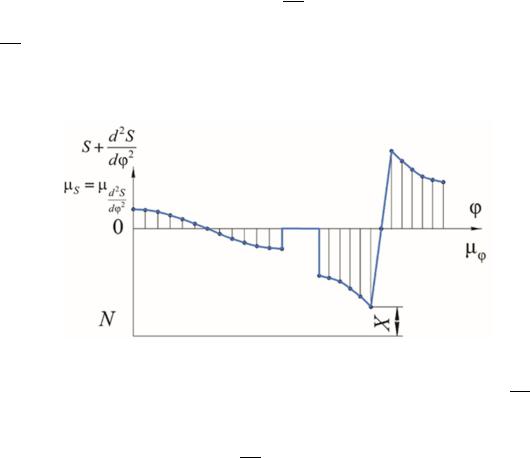
Из(4.2) следует, что R0 > – S + ddφ2S2 . С учетом этого графики S = S(φ)
и ddφ2S2 = f(φ) приводятся к одному масштабному коэффициенту μl (см.
предыдущее) и суммируются. Получают ординаты суммарного графика для определенных значений фазового угла (рис. 4.8).
Рис. 4.8. Пример определения начального радиуса R0
Учитывая то, что должно выполняться условие R0 > – S + ddφ2S2 , ось абсцисс переносится в направлении отрицательных значений ординат на расстояние, большее, чем – S + ddφ2S2 , например, на X мм в масштабе μS (см.
рис. 4.8, в). Тогда R0 = (0N) μl, где 0N расстояние в миллиметрах между старой и новой осями абсцисс (см. рис. 4.8).
4.3.3. Профилирование кулачка с плоским толкателем
Алгоритм профилирования следующий.
1. Строят окружность радиуса |
R0 |
, мм, с центром в произвольной |
|
μ |
|
точке О (рис. 4.9). |
l |
|
|
|
2.Пометодуобращенногодвижениявсторону,противоположнуювращению кулачка, от точки О на этой окружности откладывают фазовые углы, которые делят на то же количество частей, что и на диаграмме S = S(φ).
3.В общем случае при наклоне оси толкателя к его плоскости под
углом , расстояния от центра вращения кулачка до этой плоскости в любом положении равны R0 + Si sinγ . Следовательно, через точки деления для каждого положения на фазе удаления и сближения проводят лучи из
89
