
книги / Математическое моделирование дискретные подходы и численные методы
..pdf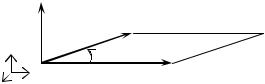
z
|
|
y |
k |
α |
x |
i |
j |
|
|
|
Рис. 1.2. Векторное произведение
обычными для чисел свойствами: x× y≠
Оба способа умножения по свойствам совершенно непохожи на привычное произведение чисел. В первом случае (1.2) результат умножения является даже не вектором, а числом (скаляром). Второе же умножение хотя и дает вектор, но не обладает
y× x , (a× b)× c≠ ×a ×(b c) . Правда,
в обоих случаях справедлив закон, называемый распределительным (с распределяется между а и b ):
(a +b) c = a c + b c , (a + b)× c= a× +c b× c .
Итак, вся основа векторного исчисления уместилась на странице, но многие теоремы, доказательство которых в «довекторные» времена требовали десятков страниц, стали доказываться в одну строчку. Открылись широчайшие возможности для решения новых задач. Появление векторов привело к бурному развитию механики, которая постепенно перестала являть собой обширный набор частных результатов, относящихся к решению конкретных задач и мало связанных между собой, а стала строиться на основе общих для этих задач принципов, сформулированных в виде аксиом, превратившись в эффективный метод исследования Природы.
Качественно новый по сравнению с векторами объект можно было бы ввести подобно тому, как происходил переход от чисел к векторам как неразделимым парам или тройкам чисел, но рассматривая уже, например, неразделимые пары векторов. Как показывает опыт, ни одно из основных понятий, вызвавшее появление новых разделов математики, не возникало формально или искусственно, все они рождались в приложениях и соответствовали реальным, практически важным объектам.
Так и векторы, родившись в механике, с самого начала стали наделяться вполне ясным физическим смыслом: вектор скорости (точки тела) v, вектор силы f, вектор момента M, вектор нормали к поверхности n и многие другие. Некоторые примеры оказались довольно необычными. Например, существует и такое понятие, как векторная площадь. При теоретическом описании поведения не абсолютно твердых, а реальных деформируемых тел в каждой их точке в любой момент времени можно построить некоторую очень малую материальную площадку (ее называют
11
элементарной). Такая площадка образуется частицами этого тела из малой окрестности выделенной точки, расположенными в одной плоскости. В силу малости форма площадки роли не играет, обычно ее считают параллелограммом (или прямоугольником). Площадь такого параллелограмма обозначатся как ∆ S (знак ∆ подчеркивает малость этой величины). В одномерном теле (например, тонком стержне или канате) эта площадка может быть ориентирована только перпендикулярно его оси. В двумерном теле (например, не слишком толстой пластине) уже существует бесконечно много способов ориентировать материальную площадку, перпендикулярную его поверхности. А в трехмерном теле привязки к какой-либо поверхности нет вообще. То есть возникает необходимость как-то задавать не только площадь, но и ориентацию площадки в пространстве. Для этого к произвольной площадке в рассматриваемой точке нужно провести единичную нормаль n (вектор, перпендикулярный плоскости площадки). Причем, не вдаваясь в детали, будем считать, что именно единичный вектор n и задает площадку, то есть любому вектору n, проведенному из данной точки, будет соответствовать единственная элементарная площадка с заданной (очень малой) площадью ∆ S. Поэтому естественным оказывается появление векторной площадки ∆S ≡ n∆ S .
Другим важным объектом векторной природы является так называемый вектор напряжений или усилий (не путать с силой). Для пояснения его физического смысла можно привести пример опытов Галилео Галилея. Исследуя прочность канатов различной толщины на разрыв, он обнаружил, что величина приложенной силы f, при которой рвется канат, является недостаточно удобной характеристикой прочности. Это вполне понятно, поскольку в ней никак не учитывалась толщина каната. Отношение f к площади поперечного сечения каната S имеет размерность Па (как и давление) и называется вектором напряжений (называемый в некоторых работах также вектором усилий) p = f / S . Это понятие впервые
было введено Галилеем и оказалось впоследствии очень плодотворным. Но во многих ситуациях появляются физические объекты более сложной природы, чем векторы. И впервые они зародились именно в механике. Для понимания того, как возникают эти объекты, поговорим немного об универсальной математической модели, позволяющей описывать и движение далеких галактик, и движение раскаленных веществ в недрах Солнца, и течение крови в сосудах, и изменение формы или даже разрушения созданных человеком объектов (строений, машин, их деталей). Используя законы Ньютона, можно описать движение материальных точек или даже
12
абсолютно твердых тел. Как теперь перейти к описанию движения реального деформируемого тела? Существует несколько основных подходов. Во-первых, отметим, что все тела, окружающие нас, состоят из огромного (дискретного) набора мельчайших взаимодействующих частиц. Записывая для каждой из них законы Ньютона с учетом законов взаимодействия этих частиц (основа дискретного подхода), мы, видимо, сможем описать поведение тела, но при этом получим систему огромного количества уравнений, решить которую для макроскопических объектов (строительных конструкций, взаимодействующих деталей двигателей и других механизмов) практически невозможно. Другой подход предоставляет статистическая физика, изучающая статистические законы распределения параметров, описывающих, например, движение и взаимодействие частиц тела. Третий подход основан на использовании модели сплошной среды (или модели деформируемого континуума). Свойства и характеристики отдельных частиц (масса, температура, скорость, ускорение и все остальные) «размазываются» по объему, который занимает тело. В результате мы имеем дело не с набором частиц, а с непрерывными распределениями (функциями) их характеристик по области пространства, занимаемой телом. Как в эту модель включить взаимодействие частиц, существовавшее до «размазывания»? Ответ на этот вопрос помогает дать принцип разрезания Эйлера–Коши: если мы рассмотрим любую элементарную площадку в теле, то предполагается, что воздействия от всех частиц, оказавшихся по одну сторону, на частицы по другую сторону площадки можно заменить действием поверхностной силы ∆ f (а в некоторых теориях – и моментом сил). То есть получается, что каждой площадке в каждой точке тела соответствует своя поверхностная сила. Как мы выяснили, при исследовании деформируемых тел рассматриваются векторные площадки ∆S = n ∆ S , то есть каждой нормали n будет соответство-
вать своя площадка и своя сила ∆ f . Чтобы ввести напряжение, можно разделить силу на скалярную величину площади и ввести напряжение в точке, зависящее от ориентации площадки: pn = ∆ f /∆ S . Здесь неслучайно
используется обозначение pn проекции. Но в этом случае ее результатом
является не число, а вектор. Так появляется необходимость в новом математическом понятии, связывающем пару векторов, – тензоре второго ранга, а в рассмотренном случае тензоре напряжений σ. «Проекция» этого объекта на нормаль n σ= pn и есть вектор напряжений. Сам тензор напряжений σ
вточке M определяется как совокупность всех возможных упорядоченных пар n и pn , заданных в точке M. И теперь вопрос об учете взаимодействия мельчайших частиц тела сводится к заданию связи тензора напряжений σ
13
и характеристик движения деформируемого континуума. Для упорядоченных пар n и pn можно было бы ввести обозначение как для компонент вектора
(упорядоченной пары чисел, только «компоненты» нового объекта сами являются векторами), например {n,pn} , но оно не вполне удобно. Для обозначения неразделимой упорядоченной пары векторов вводят символ , причем упорядоченность означает, что n pn≠ pn n (как, впрочем, и для векторного умножения). Этот знак называют диадным или тензорным
умножением, а упорядоченную пару векторов n pn |
называют диадой. За- |
метим, что в современной научной литературе знак |
для упрощения запи- |
си не ставят, предполагая, что по контексту можно понять, о каком умножении идет речь.
Термин «второго ранга» по отношению к тензору говорит о том, что он состоит из пар векторов – диад. Объект, который можно составить из одиночных векторов (то есть вектор), по аналогии естественно называть тензором первого ранга, а число – тензором нулевого ранга. Объект, составленный из упорядоченных троек векторов, так называемых «триад» a b c , будет представлять собой тензор третьего ранга.
Впервые тензоры были введены Леонардом Эйлером в 1758 году (тензор инерции твердого тела, тензор поворота). Хотя термин «тензор» был введен только в 1900 году по предложению В. Фойгта (W. Voight), сам Л. Эйлер работал с этими объектами так же, как ученые работают с тензорами сегодня. Важно отметить, что Л. Эйлер был уникальным человеком – он на формальном уровне не владел многими стандартными ныне математическими методами, но тем не менее по числу новых фундаментальных результатов ему нет равных в истории человечества. Это частично объясняется тем, что Л. Эйлер обладал совершенно феноменальной интуицией и способностью представления образов вводимых им объектов. А тензор напряжений, о котором мы говорили, впервые был введен значительно позже, как и некоторые другие тензоры (тензор деформаций, тензор упругих свойств), знаменитым французским математиком Огюстеном Луи Коши в 1822 году и является самостоятельной сущностью, имеющей ясный физический смысл. Введенный выше тензор напряжений так и называется – тензор напряжений Коши. Разберемся с понятием тензора детальнее.
Свойства диадного произведения. Тензоры второго ранга. Тен-
зорное произведение может связывать в новый объект только векторы или тензоры, а если появляется произведение скалярной величины k (числа) на вектор a: k a , то результатом будет вектор ka . При ска-
14

лярном умножении диады a |
b на вектор с слева на первом месте |
|||
в диаде |
появляется |
скаляр |
– |
результат скалярного произведения: |
c a b= |
(c a) =b |
(c a)=b |
k1b . На втором месте в диаде при этом ос- |
|
тается неизменным вектор b . При скалярном умножении диады a b на вектор с справа на первом месте в диаде остается вектор а, а на вто-
ром |
месте |
появляется скаляр – результат |
скалярного |
произведения: |
|||
a b |
c= a |
(b =c) |
a(b =c) |
ak=2 k2a . Это помогает понять, почему в об- |
|||
щем случае n p ≠ |
p |
n |
n . |
|
|
||
|
|
n |
|
|
|
|
|
Все множество произвольных диад a |
b образует, |
подобно векто- |
|||||
рам, так называемое линейное пространство, то есть множество объектов, для которых выполняются правила (аксиомы):
α (a |
b) = (α a) b = a |
(α b) = α a b , |
(1.4) |
(α + β )a |
b = α a b + β a |
b = β a b + α a b . |
(1.5) |
Аксиомой (1.5) введено правило сложения двух одинаковых диад (при этом будут складываться их коэффициенты). Из этой же аксиомы следует, что слагаемые в сумме диад можно переставлять местами. Из (1.4) при α = 0 имеем
|
0(a b) = 0 b = a 0 , |
(1.6) |
при этом, полагая в (1.5) β =1, получим |
|
|
|
0(a b) + a b = a b , |
|
то есть диада 0(a |
b) является нулем в пространстве диад, как обычный 0 |
|
в пространстве чисел. Следующие аксиомы |
|
|
(a + b) |
c = a c + b c , a (c + b) = a c + a b |
(1.7) |
позволяют складывать диады, если у них либо левые, либо правые векторы совпадают. При этом сумма таких диад сама является диадой. А что будет в случае, когда складываются диады, составленные из совершенно разных векторов:
a b+ c d ?
Результат этой операции является более сложным объектом, чем диада – тензором второго ранга. Его уже нельзя представить в виде диадного произведения двух векторов. В наиболее общем виде он представим
15
как неупорядоченная сумма (слагаемые могут быть записаны в любом порядке) упорядоченных пар векторов (диад):
T = a |
(1) |
|
(1) |
a |
(2) |
(2) |
(3) |
b+ |
(3) |
... |
(1.8) |
|
b + |
|
b+ |
a |
|
Очевидно, что диада является частным случаем тензора второго ранга:
a b= a +b +0 +0 ... .
Для тензоров второго ранга выполняются аналогичные аксиомы:
α T= α a |
b+ α |
a |
(2) |
+bα |
(2) |
a + b |
(3) |
..., |
(1) |
(1) |
|
|
(3) |
|
(α + β )T = α T+ β T .
Сумма любых тензоров второго ранга является тензором второго ранга (в отличие от диад). Это элементарно показывается, если разложить все векторы по одному и тому же базису (тройке ортонормированных векторов в трехмерном пространстве i, j, k) и использовать рассмотренные аксиомы диад.
Для скалярного произведения тензоров справедливо
A B ≠ B A . |
(1.9) |
Кроме скалярного умножения, используется векторное умножение тензора A на вектор c слева или справа:
c × A= |
n |
|
b =) |
n |
|
) |
=b |
|
n |
|
b |
|
, |
c× (∑i=1a |
∑i=1×(c a |
(i) |
∑i=1q |
(i ) |
(i ) |
||||||||
|
|
(i ) |
(i) |
|
(i) |
|
|
|
|
|
|||
A × c= (∑in=1a(i ) |
|
b(i×) ) =c ∑in=1a(i) |
(×b(i )= c) |
∑in=1a(i) |
r(i) . |
||||||||
Как видно, при векторном умножении тензора второго ранга на вектор получается тензор второго ранга.
Часто встречающейся характеристикой тензора второго ранга является его след trA (от английского trace), который является скаляром вида:
trT = tr(a |
(1) |
|
(1) |
a |
(2) |
(2) |
(3) |
b+ |
(3) |
=...) |
|
b + |
|
b+ |
a |
|
= a(1) b(1) + a(2) b(2) + a(3) b(3) + ...
Для тензоров второго ранга вводится и такая операция, как транспонирование: AT . Для диад она приводит к смене мест векторов диады:
16
PNRPU
|
|
|
(a b)T= b |
a , |
((a b)T )T= a |
b , |
|
|
|
||||||||
|
(1) |
|
(1) |
|
(2) |
(2) |
T |
(1) |
|
(1) |
|
(2) |
|
(2) |
|
|
|
(a |
|
a |
...=) |
|
+a |
b |
+a |
... |
(1.10) |
||||||||
|
b + |
|
b+ |
|
b |
|
|
|
|||||||||
При транспонировании скалярного произведения тензоров второго ранга сами тензоры меняются местами и транспонируются:
(A B)T = BT AT .
Тензор A можно скалярно умножить на вектор a слева, a A , или справа, A a , причем a A ≠ A a . Но для этого умножения выполняется
a A = AT a .
Тензор второго ранга A называется симметричным, если для него
выполняется |
|
AT = A . |
(1.11) |
При этом будет справедливо равенство
a A = A a .
Примерами симметричных тензоров второго ранга являются тензоры
a a , a b + b a .
Важным примером симметричного тензора второго ранга является единичный тензор E , такой что
a E = E a = a a , |
(1.12) |
где обозначает так называемый квантор общности («для любого»). Аналогичное правило выполняется и для тензоров:
A E = E A = A A . |
(1.13) |
Единичный тензор может быть записан по-разному. В частности, по- |
|
лезно знать следующее его представление: |
|
E = m m + n n + p p , |
(1.14) |
где m, n, p – любые (и это очень важно!) единичные попарно ортогональные векторы (в частности, m m = 1, но m n = 0 и m p = 0 ), в качестве
которых могут быть выбраны, например, орты i, j, k координатных осей.
17
Выше было показано, что в результате скалярного умножения тензора второго ранга на вектор получается новый вектор. Поэтому каждый тензор второго ранга можно воспринимать как некоторое действие, переводящее один вектор в другой. В математике такие действия (удовлетворяющие перечисленным для тензоров аксиомам) называют линейными операторами. Любой вектор x можно представить в виде суммы трех взаимно ортогональных векторов, полученных, например, с помощью упомянутых выше векторов m, n, p – x = x1 + x2 + x3 , где x1 = (x m)m , x2 = (x n)n , x3 = (x p)p . Такие преобразования, как поворот, растяжение
или их комбинация, переводящие вектор p = p1 + p2 + p3 ( pi попарно пер-
пендикулярны) в вектор d = d1 + d2 + d3 |
|
(di попарно перпендикулярны), |
|||||||||
представляются как тензор второго ранга Q вида |
|
|
|
||||||||
Q = |
|
1 |
d1 p1 + |
1 |
d2 |
|
p2 + |
|
1 |
d3 p3 . |
(1.15) |
|
|
|
|
|
|||||||
p1 |
p1 |
|
p3 |
|
|||||||
|
|
p2 p2 |
|
|
p3 |
|
|||||
Действительно, |
Q p = d . |
Преобразование растяжения в k раз есть |
|||||||||
тензор kE . Также можно построить тензор, задающий поворот на угол ϕ ( −π < ϕ < π ) относительно оси, направление которой определяется единичным вектором m. Структура этого ортогонального тензора задается теоремой Эйлера [7], которая говорит, что тензор поворота Q произвольного вектора x относительно оси m ( Q x ) имеет вид
Qmϕ = m |
m+ |
(E− |
m |
m)cos ϕ + m × (E− m |
m)sin ϕ = |
|
= m |
m+ |
(E− |
m |
m)cosϕ + |
× m Eϕ=sin |
(1.16) |
= m |
m(1− |
cosϕ +) |
Ecosϕ + |
×m Eϕsin . |
|
|
Строгое доказательство этой теоремы можно найти в [7], здесь же мы рассмотрим геометрическую интерпретацию теоремы на основе первого представления в (1.16). При действии тензора поворота Qmϕ на про-
извольный вектор x первое слагаемое m m из первого представления тензора поворота (1.16) оставляет неизменной составляющую вектора x,
направленную вдоль оси m ( m m x= xmm – при повороте вокруг оси
m она не изменяется, рис. 1.3). Второе слагаемое укладывает «оставшуюся часть» вектора в плоскость, перпендикулярную оси m, и уменьшает за счет поворота на угол ϕ часть вектора x, лежащую в этой плоскости и направленную вдоль оси l. Направление оси l совпадает с направлением
18
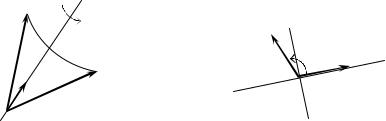
(E − m m) x . Третье слагаемое описывает появление (за счет поворота) составляющей нового (повернутого) вектора вдоль оси k, перпендикулярной проекции вектора x на рассматриваемую плоскость. В итоге получаем
|
x' = Qmϕ x . |
|
|
(1.17) |
x |
O |
|
|
|
(E − m m) x' |
k |
|
|
|
|
|
|
||
|
|
|
ϕ |
l |
|
|
|
(E − m m) x |
|
|
x ' |
O |
|
|
|
|
|
|
а |
б |
Рис. 1.3. Поворот вектора вокруг оси m: а – поворот в пространстве;
б – на плоскости, ортогональной вектору m (вид из точки O на конце оси m)
Используя теорему Эйлера, получим правило наложения поворотов. Идея очень проста: повернем вектор x вокруг оси m на угол ϕ 1 и получим
вектор Qmϕ 1 x , а затем повернем полученный вектор еще и на угол ϕ 2 относительно той же оси m, тогда
x' = Qmϕ 2 (Qmϕ 1 x)= Qmϕ 2 Qmϕ 1 x .
Значит, общий поворот можно представить через произведение двух тензоров поворота:
(m |
m+ |
(E− |
m |
m)cos ϕ 2 + m × Esin ϕ 2 ) (m m+ |
||||||||
|
+(E − m |
m)cosϕ |
+1 |
|
m× |
Esinϕ =1 ) |
|
|
|
|||
= m |
m+ |
(E− |
m |
m)cosϕ |
2 cosϕ + |
1 × m Eϕ cosϕ 2+sin |
1 |
|||||
+m × |
Esinϕ |
2 cosϕ −1 (−E |
|
m |
m)ϕsin ϕ2 sin= |
1 |
|
|
||||
= m m+ |
(E− |
m |
m)cos(ϕ + ϕ |
+ |
2 |
) × m Eϕ sin(+ ϕ = |
2 |
) |
Qϕ 1+ϕ 2 . |
|||
|
|
|
|
1 |
|
|
2 |
|
m |
|||
Q = Qmϕ 2 Qmϕ 1 = Qmϕ 1 +ϕ 2 .
19
В преобразованиях использовались соотношения, в которых принималось, что для попарно ортогональных единичных векторов m, n, p выполня-
ется (m × n= p , m × p= − n , n × p= m ):
m m m m= m m ,
m m (E− m |
m=) (−E m m) m= m m− m |
=m m 0 , |
|
||||||||||
m m (m× E=) m |
|
3 |
|
|
|
3 |
m× (m e=) |
e |
|
0 , |
|||
m ×m e |
i |
= e |
m |
i |
|||||||||
|
|
∑ |
|
i |
∑ |
|
|
|
i |
|
|
||
|
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|
|
|
(E − m m) (E− m |
m=) −E 2m +m m= m− E |
m m , |
|
||||||||||
|
(m × E) m m= m× m =m 0 , |
|
|
|
|
|
|
||||||
(E − m m) (m× E=) |
m× −E m |
|
3 |
|
)= e × |
|
|
|
|
||||
m ×(m |
e |
m E , |
|
||||||||||
|
|
|
|
|
∑ |
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
m × E (E− m m=) m× −E ×m m = m× m E ,
m × E= m× (m +m n + n p= p)× (m +n) ×n (m= p) −p p n n p , m× E (m× E=) (p −n n p) (p− n =n − p) − p =p − n −n (E m m).
Итак, при наложении поворотов относительно одной оси углы будут складываться. Этот же ответ подсказывает и интуиция. Но в большинстве случаев, когда накладываются повороты относительно разных осей в пространстве, интуиция уже перестает работать, но правило перемножения ортогональных тензоров поворота выполняется всегда:
Q = Qϕ 2 Qϕ 1 .
m2 m1
При повороте двух векторов на один и тот же угол относительно одной и той же оси результат векторного произведения «повернутых» векторов будет равен повороту вектора, полученного векторным произведением исходных векторов:
(Q a) × (Q b)= Q (a× b) .
Отметим еще одну особенность тензора поворота: при повороте «повернутого» вектора в противоположном направлении на тот же угол вокруг той же оси мы получим исходный вектор. Такое действие (или пре-
образование вектора) называется обратным и обозначается как Q−1 :
20
