
книги / Теория сварочных процессов
..pdfизображении, кодированные числом, меньшим k, на бинарном изображении станут белыми, в матрице – кодировка 0; все темные участки на реальном изображении, кодированные числом, большим k, на бинарном изображении станут черными, в матрице – кодировка 1;
2) выделить на изучаемом шлифе квадратный участок площадью 300×300 пикселей (в зависимости от увеличения и типа металлографического микроскопа это может соответствовать площади от 10 мкм2 до 1 мм2). Это значение площади в пикселях является оптимальным. Участки меньших размеров не желательны, поскольку могут охватывать только отдельный структурный фрагмент и не дать полного представления о периодичности и фрагментарности структуры в целом. Верхняя граница площади обрабатываемого фрактальным анализом участка шлифа определяется только возможностями процессора компьютера;
3) полученные изображения структур образцов сохранить в формате точечного рисунка bmp или jpg.
После этих подготовительных действий можно приступать собственно к проведению анализа, последовательные этапы которого задаются алгоритмом, разработанным на кафедре СП и ТКМ ПГТУ.
При фрактальном описании структур сварных швов алгоритм, реализованный программными средствами Mathcad 2001 Professional, MATLAB 6.1, заключался в следующем:
1.Дискретная аппроксимация исследуемых структур: разбиение соответствующих бинарных изображений квадратной сеткой, состоящей из одинаковых ячеек, и присвоение ячейкам, приходящимся на область перлита, значений 0, а на однофазную светлую область видманштеттова феррита – значений 1. Таким образом, полученное оцифрованное изображение структуры представляет собой матрицу, состоящую из нулей и единиц.
2.Обработка массивов цифровых значений (матриц), полученных
путем разбиения матриц на более крупные ячейки с размерами Li×Li
(i = 1…32).
3.Построение для каждого разбиения характеристической меры
ввиде вероятности распределения единиц Pi, необходимых для покрытия поля феррита.
4.Аппроксимация зависимостей ln(Pi) от ln(Li) методом наимень-
ших квадратов и определение фрактальных размерностей Df, из соот-
ношения
Pi = const(Li)–D.
141
Данный алгоритм был реализован для анализа структурообразования металла швов опытных электродов серии 17 (по нумерации УИС), с покрытием на основе уральского ильменита. В качестве базового состава использовали электроды марки МР-3, с заменой ферромарганца на силикомарганец и добавкой ферротитана.
Для исследования микроструктуры использовали микроскоп МИМ-8, цифровую видеокамеру AverMedia (разрешение 640×420), транслирование изображения на дисплей компьютера осуществлялось системой Amcap.
Фрактальный анализ структур сварных швов проводился по основным зонам сварного соединения:
–по центру шва;
–зоне термовлияния (ЗТВ);
–зоне сплавления;
–основному металлу.
Изучали фотоизображения всех зон сварного соединения размером 440×440 пикселей, что соответствовало участку сварного шва 150×150 мкм (при увеличении ×150). Такой размер охватываемой области вполне корректен, так как толщина зон, в которых имеются структурные отличия может достигать 400 мкм (за исключением зоны сплавления). Дополнительно исследовали фотоизображения центра шва при большем увеличении (×450), размер изображения составлял 300×300 пикселей, что соответствовало участку образца размером 40×40 мкм. На рис. 4.18–4.22 представлен листинг программы бинаризации структуры центра шва опытных электродов серии 17.
Приведенный фрагмент матрицы М соответствует реальному изображению структуры, а фрагмент матрицы Mb – бинарному изображению. Полученное бинарное изображение обрабатывалось программой фрактального анализа, приведенной на рис. 4.23, листинг обработки приведен на рис. 4.24–4.27.
В результате реализации программного алгоритма получено значение фрактальной размерности структуры Df .
Результаты фрактального анализа структуры металла шва приведены в табл. 4.3, где представлены структуры различных зон наиболее характерных из сварных швов и соответствующие им фрактальные размерности.
Как видно из сопоставления значений фрактальной размерности Df с топографией структуры (см. табл. 4.3), более грубая структура имеет меньшее значение фрактальной размерности, а более гомогенная структура имеет большее значение фрактальной размерности (исключение составляет только зона сплавления, результаты анализа которой объяснены ниже).
142

Считывание изображения M  READBMP ( "1793center3.bmp")
READBMP ( "1793center3.bmp")
|
Число строк rows (M) = 640 и столбцов cols (M) = 480 матрицы М |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Выделение квадратной матрицы из |
|
|
|
|
Трансформирование матрицы в бинарный |
||||||||||||||||||||||||||||
|
считываемого массива (изображения) |
|
|
|
массив (0; 479) |
---> (0;1) |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
M |
|
submatrix( M ,i1,i2,j1, j2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
M |
|
submatrix ( M ,40,370,170,500) |
|
|
|
|
|
|
|
|
c |
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
Mb |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
for |
i 0.. rows ( M ) |
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
for j 0.. cols ( M ) |
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dj ,i |
0 if Mj ,i <k |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
if Mj ,i |
k |
|
|
|
||||
|
WRITEBMP ("1793center3_bin.bmp" |
) |
Mb .255 |
|
|
|
|
|
c |
c |
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
. |
|
|
5 6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
13 |
14 |
15 |
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
255 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
20 |
20 |
17 |
18 |
19 |
18 |
22 |
13 |
22 |
23 |
24 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
||||
|
|
|
1 |
20 |
20 |
20 |
26 |
24 |
21 |
21 |
19 |
28 |
24 |
46 |
|
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
2 |
20 |
19 |
19 |
21 |
16 |
13 |
17 |
30 |
41 |
51 |
51 |
|
2 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
3 |
20 |
24 |
23 |
12 |
15 |
23 |
28 |
60 |
57 |
53 |
51 |
|
3 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
4 |
20 |
19 |
19 |
5 |
17 |
37 |
42 |
79 |
60 |
40 |
33 |
|
4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
5 |
20 |
24 |
18 |
24 |
31 |
53 |
67 |
97 |
82 |
57 |
53 |
|
5 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
M = |
6 |
20 |
19 |
14 |
63 |
57 |
70 |
84 |
89 |
83 |
63 |
62 |
Mb = |
6 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
||||
|
|
|
7 |
20 |
29 |
38 |
138 |
128 |
125 |
123 |
88 |
80 |
61 |
61 |
|
7 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
8 |
20 |
44 |
58 |
150 |
137 |
133 |
126 |
91 |
74 |
52 |
51 |
|
8 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
9 |
15 |
146 |
161 |
85 |
63 |
128 |
111 |
115 |
109 |
63 |
79 |
|
9 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|||
|
|
|
10 |
67 |
184 |
174 |
58 |
68 |
119 |
101 |
158 |
113 |
81 |
111 |
|
10 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
|
||||
|
|
|
11 |
150 |
137 |
116 |
113 |
148 |
79 |
64 |
202 |
142 |
126 |
146 |
|
11 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
|
||||
|
|
|
12 |
141 |
107 |
92 |
141 |
182 |
58 |
41 |
192 |
140 |
140 |
137 |
|
12 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
|
||||
|
|
|
13 |
114 |
136 |
100 |
126 |
163 |
51 |
38 |
169 |
110 |
104 |
95 |
|
13 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
Рис. 4.18. Листинг программы бинаризации структуры центра сварного шва электрода 1793 (вверху); фрагменты матриц изображения структуры (в центре); структуры центра шва (внизу): реальная (а) и бинарная (б). ×150
143
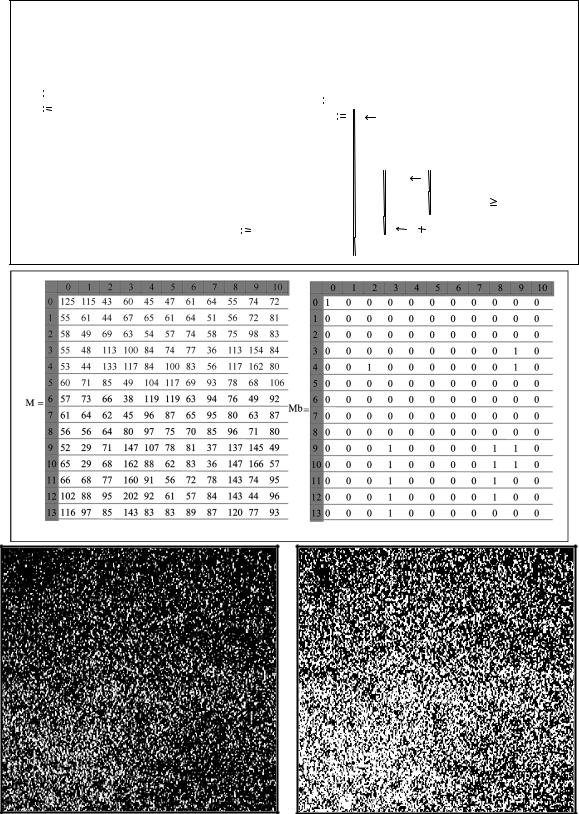
Считывание изображения M  READBMP ( "1793ztv.bmp")
READBMP ( "1793ztv.bmp")
Число строк rows (M) = 640 и столбцов cols (M) = 480 матрицы М |
|
|
|
|
|
|
|||||||
Выделение квадратной матрицы из |
|
Трансформирование матрицы в бинарный |
|||||||||||
считываемого массива (изображения) |
массив (0; 479) |
---> (0;1) |
|
|
|
|
|||||||
M |
|
submatrix( M ,i1,i2,j1, j2) |
|
|
|
|
|
||||||
|
|
k |
|
150 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
M |
|
submatrix ( M ,40,370,170,500) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
Mb |
c |
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
for |
i 0.. rows ( M ) |
|
1 |
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
for j 0.. cols ( M ) |
|
|
1 |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Dj ,i |
0 if Mj ,i <k |
|||||
|
|
|
|
|
|
|
|
|
1 if Mj ,i |
k |
|||
WRITEBMP ("1793ztv_bin.bmp" |
) |
Mb .255 |
|
c |
c |
1 |
|
|
|
|
|||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
а |
б |
Рис. 4.19. Листинг программы бинаризации структуры ЗТВ сварного шва электрода 1793 (вверху); матрицы изображения структуры (в центре); структуры ЗТВ (внизу): реальная (а) и бинарная (б). ×150
144

Считывание изображения M  READBMP ( "1793line_spl.bmp")
READBMP ( "1793line_spl.bmp")
Число строк rows (M) = 640 и столбцов cols (M) = 480 матрицы М
Выделение квадратной матрицы из |
|
|
Трансформирование матрицы в бинарный |
|
|
|
||||||||||||||||||||||||||||||
считываемого массива (изображения) |
|
|
массив (0; 479) |
---> (0;1) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
M |
|
|
|
submatrix( M ,i1,i2,j1, |
j2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
M |
|
|
submatrix ( M ,40,370,170,500) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Mb |
|
|
|
c |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
for i 0.. rows ( M ) |
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
for |
j 0.. cols ( M ) |
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dj ,i |
0 if Mj ,i <k |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
if Mj ,i |
k |
|
|
|
|
||||
WRITEBMP ("1793line_spl_bin.bmp" ) |
|
Mb .255 |
|
|
|
|
|
D |
|
c |
c |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
|
|||||||
|
0 |
74 |
66 |
67 |
73 |
66 |
58 |
59 |
54 |
64 |
74 |
63 |
|
0 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
1 |
56 |
49 |
68 |
95 |
73 |
55 |
75 |
71 |
67 |
72 |
58 |
|
1 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
2 |
52 |
42 |
70 |
101 |
64 |
53 |
98 |
92 |
59 |
76 |
67 |
|
2 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
3 |
80 |
60 |
87 |
113 |
66 |
70 |
127 |
99 |
68 |
89 |
86 |
|
3 |
0 |
|
|
0 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
4 |
97 |
66 |
89 |
116 |
71 |
76 |
118 |
76 |
86 |
92 |
78 |
|
4 |
0 |
|
|
0 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
5 |
104 57 |
75 |
94 |
57 |
60 |
87 |
64 |
77 |
71 |
56 |
|
5 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
|||||
M = |
6 |
96 |
56 |
79 |
82 |
46 |
53 |
76 |
77 |
68 |
60 |
48 |
Mb = |
6 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
7 |
71 |
54 |
91 |
80 |
43 |
54 |
66 |
77 |
87 |
66 |
52 |
|
7 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
8 |
63 |
62 |
80 |
73 |
42 |
48 |
72 |
66 |
88 |
66 |
55 |
|
8 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
9 |
57 |
54 |
79 |
77 |
45 |
57 |
92 |
90 |
89 |
64 |
48 |
|
9 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
10 |
59 |
50 |
71 |
72 |
46 |
64 |
98 |
94 |
89 |
66 |
55 |
|
10 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
11 |
70 |
52 |
53 |
54 |
50 |
71 |
89 |
83 |
72 |
64 |
67 |
|
11 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
12 |
67 |
57 |
43 |
42 |
58 |
73 |
78 |
82 |
62 |
67 |
80 |
|
12 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
13 |
55 |
60 |
49 |
43 |
58 |
62 |
62 |
80 |
69 |
75 |
84 |
|
13 |
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
0 |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗТВ
К центру шва |
|
а |
б |
Рис. 4.20. Листинг программы бинаризации структуры зоны сплавления сварного шва электрода 1793 (вверху); матрицы изображения структуры (в центре); структуры зоны сплавления (внизу): реальная (а) и бинарная (б). ×150
145

Считывание изображения M  READBMP ( "1793osn.bmp" )
READBMP ( "1793osn.bmp" )
Число строк rows (M) = 640 и столбцов
Выделение квадратной матрицы из считываемого массива (изображения)
M submatrix( M ,i1,i2,j1, j2)
M  submatrix ( M ,40,370,170,500)
submatrix ( M ,40,370,170,500)
WRITEBMP ("1793osn_bin.bmp" )  Mb
Mb
cols (M) = 480 матрицы М
Трансформирование матрицы в бинарный
массив (0; 479) |
---> (0;1) |
|
|
|
|
|||||
k |
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
Mb |
c |
0 |
|
|
|
|
|
|
|
|
|
|
for |
i 0.. rows ( M ) |
|
1 |
|
||||
|
|
|
|
|||||||
|
|
for j 0.. cols ( M ) |
|
|
1 |
|||||
|
|
|
||||||||
|
|
|
Dj ,i |
0 |
if Mj ,i <k |
|||||
|
|
|
|
|
1 |
if Mj ,i |
k |
|||
.255 |
|
D |
c |
c |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
0 |
39 |
63 |
38 |
45 |
39 |
39 |
34 |
92 |
133 |
124 |
37 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
1 |
55 |
44 |
57 |
37 |
56 |
35 |
35 |
129 |
91 |
54 |
70 |
|
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
2 |
47 |
44 |
49 |
46 |
53 |
44 |
39 |
120 |
86 |
78 |
102 |
|
2 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
3 |
51 |
57 |
45 |
42 |
18 |
106 |
89 |
38 |
54 |
170 |
149 |
|
3 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
4 |
86 |
69 |
45 |
42 |
0 |
148 |
139 |
24 |
84 |
178 |
170 |
|
4 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
|
|
|
|
5 |
60 |
155 |
129 |
32 |
59 |
134 |
122 |
104 |
155 |
129 |
76 |
|
5 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
|
|
|
M = |
6 |
23 |
173 |
164 |
20 |
78 |
97 |
81 |
103 |
137 |
86 |
71 |
Mb = |
6 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
|
|
|
|
7 |
23 |
82 |
66 |
39 |
44 |
42 |
41 |
42 |
52 |
61 |
97 |
|
7 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
8 |
51 |
44 |
38 |
39 |
40 |
54 |
53 |
28 |
29 |
85 |
96 |
|
8 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
9 |
48 |
42 |
31 |
54 |
106 |
116 |
79 |
45 |
61 |
128 |
86 |
|
9 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
|
|
|
|
10 |
46 |
54 |
36 |
92 |
145 |
109 |
68 |
50 |
73 |
117 |
55 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
|
|
|
|
|
11 |
55 |
47 |
34 |
76 |
103 |
54 |
59 |
42 |
51 |
94 |
47 |
|
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
|
12 |
78 |
31 |
53 |
58 |
52 |
44 |
50 |
44 |
45 |
72 |
84 |
|
12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
|
13 |
122 |
56 |
45 |
55 |
68 |
62 |
32 |
80 |
119 |
59 |
32 |
|
13 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а б
Рис. 4.21. Листинг программы бинаризации структуры основного металла (вверху); матрицы изображения структуры (в центре); структуры основного металла (внизу):
реальная (а) и бинарная (б). ×150
146

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
0 |
|
1 |
|
2 |
3 |
4 |
5 |
|
6 |
|
7 |
|
8 |
|
9 |
10 |
|
|
0 |
|
21 |
20 |
20 |
21 |
21 |
22 |
15 |
15 |
29 |
20 |
21 |
|
|
0 |
0 |
|
0 |
|
0 |
|
0 |
0 |
0 |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
1 |
|
21 |
20 |
20 |
21 |
21 |
21 |
18 |
18 |
23 |
15 |
27 |
|
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
|
2 |
|
21 |
21 |
21 |
21 |
21 |
21 |
18 |
15 |
25 |
19 |
25 |
|
2 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
|
3 |
|
21 |
21 |
21 |
21 |
21 |
21 |
27 |
18 |
16 |
7 |
13 |
|
3 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
|
4 |
|
21 |
21 |
21 |
21 |
21 |
21 |
20 |
19 |
4 |
7 |
39 |
|
4 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
|
5 |
|
21 |
21 |
21 |
21 |
21 |
21 |
19 |
22 |
29 |
58 |
113 |
|
5 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
M = |
6 |
|
21 |
22 |
22 |
21 |
21 |
21 |
21 |
22 |
98 |
119 |
115 |
Mb = |
6 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
|
7 |
|
21 |
22 |
22 |
21 |
21 |
20 |
37 |
50 |
232 |
219 |
88 |
|
7 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
|
||||||
|
8 |
|
23 |
15 |
17 |
2 |
28 |
11 |
40 |
208 |
239 |
133 |
156 |
|
8 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
|
||||||
|
9 |
|
20 |
15 |
25 |
20 |
76 |
79 |
133 |
142 |
111 |
142 |
228 |
|
9 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
|
||||||
|
|
10 |
22 |
16 |
26 |
38 |
121 |
113 |
101 |
70 |
76 |
168 |
208 |
|
|
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
|
||||||
|
|
11 |
27 |
0 |
56 |
133 |
202 |
136 |
111 |
98 |
94 |
120 |
165 |
|
|
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
|
|
12 |
35 |
4 |
136 |
228 |
231 |
151 |
154 |
142 |
85 |
56 |
163 |
|
|
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||||||
|
|
13 |
34 |
52 |
229 |
241 |
184 |
163 |
168 |
149 |
115 |
123 |
203 |
|
|
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
б |
Рис. 4.22. Листинг программы бинаризации структуры центра сварного шва электрода 1807 (вверху); матрицы изображения структуры (в центре); структуры центра шва (внизу): реальная (а) и бинарная (б). ×150
147
clear a |
|
end;%for |
clear N |
|
if cnt>0; |
clear NL |
|
break; |
clear EL |
|
end; |
a = imread('1802center_bin.bmp','bmp'); |
|
end;%for |
B1=uint8(a); |
|
if cnt>0 |
SS = B1 ~= 0; |
|
N(L)=N(L)+1; |
figure, imshow(SS, 'notruesize'); |
|
end;%if |
%pause; |
|
end;%for |
p=430; |
|
end;%for |
S(1:p,1:p)=1; |
|
end; |
for i=1:p; |
|
% |
for j=1:p; |
|
% |
S(i,j)=SS(i,j); |
|
for L=1:Lmax; |
end; |
|
EL(L)=log(L); |
end; |
|
NL(L)=log(N(L)); |
Lmax=round(p/16); |
|
end;%for |
N(1:Lmax)=0.0; |
|
pP=polyfit(EL(1:Lmax),NL(1:Lma |
NL(1:Lmax)=0.0; |
|
x),1); |
EL(1:Lmax)=0.0; |
|
ff=polyval(pP,EL); |
NN=sum(S); |
|
D=pP(1) |
NMN=sum(NN); |
|
axis auto; |
N(1)=p^2-sum(NMN) |
|
figure, |
for L=2:Lmax; |
|
plot(EL(1:Lmax),NL(1:Lmax)); |
B=floor(p/L); |
|
title(['D = ',num2str(D),'']); |
for i=1:B; |
|
xlabel(['D = ',num2str(D),'']); |
for j=1:B; |
|
l=1 |
cnt=0.0; |
|
DD=N(1) |
xb=L.*(i-1)+1; |
|
l=2 |
xe=L.*i; |
|
DD=N(2) |
yb=L.*(j-1)+1; |
|
l=4 |
ye=L.*j; |
|
DD=N(4) |
for x=xb:xe; |
|
l=8 |
for y=yb:ye; |
|
DD=N(8) |
if S(x,y)==0 |
|
|
cnt=cnt+1; |
|
|
end;%if |
|
|
if cnt>0; |
|
|
|
|
|
Рис. 4.23. Реализация алгоритма программы фрактального анализа структуры металла сварного шва на языке Pascal
148
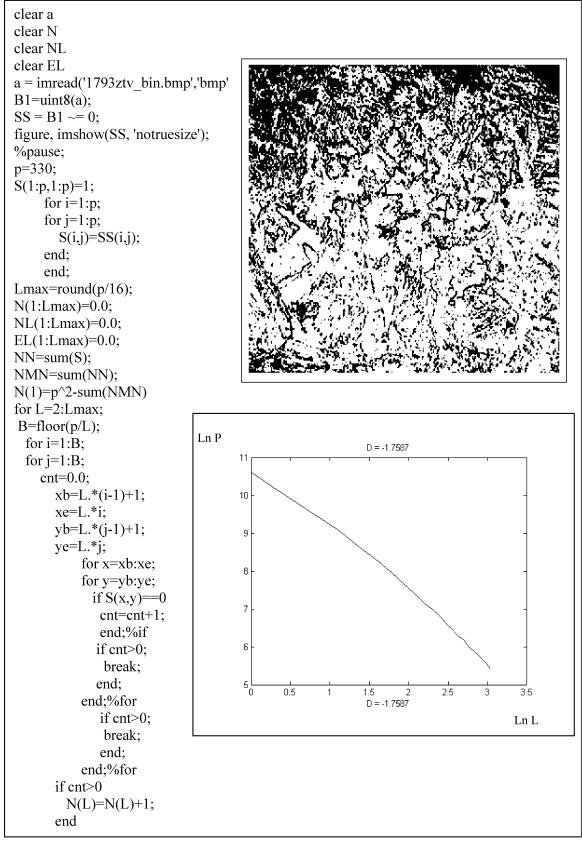
Рис. 4.24. Листинг программы фрактального анализа бинарного изображения структуры центра шва электрода 1793
149
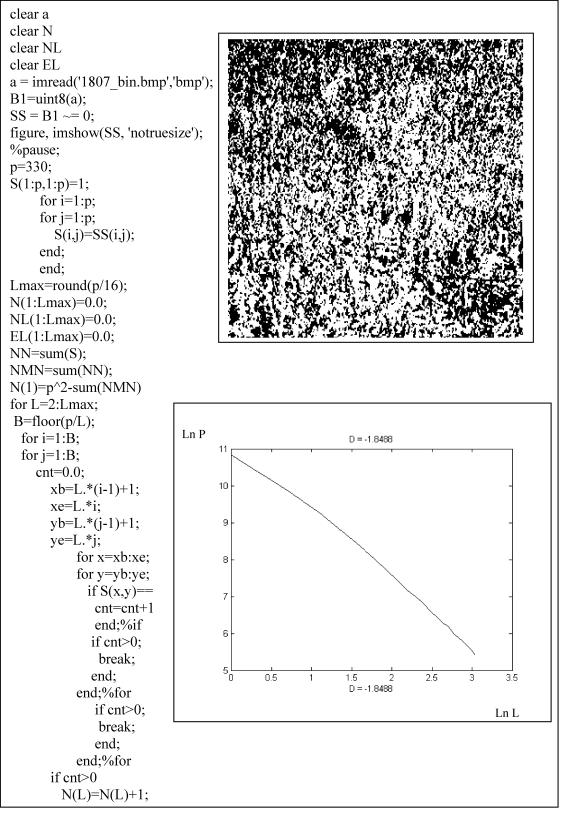
Рис. 4.25. Листинг программы фрактального анализа бинарного изображения структуры центра шва электрода 1807
150
