ctg 3x → ∞ при x → |
0 . |
|
Записав данную функцию как дробь |
x |
, получаем неопре- |
|
|
tg 3x |
деленность вида 0 , которую раскрываем по правилу Лопиталя: 0
|
|
|
|
|
|
|
|
lim x ctg 3x = lim |
x |
= lim |
1 |
= |
1 |
, |
|
3 |
|
x→ 0 |
→x 0 tg 3x → x 0 |
3 |
|
cos2 3x
так как lim cos2 3x =1.
x→ 0
Задача 6.
Найти lim ( x3 ln x).
x→ 0
Решение
Здесь мы имеем неопределенность вида 0 ∞ . Представим произведение функций в виде частного (формула 4.12), а затем,
получив неопределенность вида ∞∞ , применимправило Лопиталя:
lim ( x3 ln x) = lim |
|
|
|
|
|
1 |
|
|
|
|
ln x |
|
|
|
|
= − |
1 |
lim x3 = 0. |
= lim |
|
x |
|
−3x−4 |
|
x→ 0 |
→x 0 |
|
1 → |
x 0 |
→ 3 x 0 |
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
Задача 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти lim |
x |
|
− |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ 1 x −1 |
|
ln x |
|
|
|
|
|
|
|
Решение |
|
|
|
x → 1 являются бесконечно большими |
Здесь обе дроби при |
величинами, т.е. получается неопределенность вида ∞ − ∞ . Приведя выражение в скобках к общему знаменателю, получим:
lim |
|
x |
|
− |
1 |
|
= lim |
x ln x − x +1 |
, |
|
|
|
x→ 1 |
x −1 |
|
ln x |
→x 1 ( x −1) ln x |
т.е. неопределенность вида 0 . Применяя правило Лопиталя два
0
раза подряд и выполняя элементарные преобразования, находим:
|
x ln x − x +1 |
|
|
|
ln x + x |
1 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
lim |
= lim |
|
|
|
|
|
x |
|
|
= lim |
= |
( x −1) ln x |
|
|
1 |
|
|
|
|
|
|
|
|
|
x→ 1 |
→x 1 ln x + |
( x −1) → |
x 1 ln x +1 − |
1 |
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
= |
|
|
= lim |
|
|
|
|
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
0 |
|
x→ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x2 |
|
|
|
|
|
|
|
|
Задача 8.
Найти lim ( x − ln3 x).
x→+∞
Решение
|
Так как |
x → +∞ |
|
и ln3 x → +∞ |
, |
|
то имеем неопределенность |
|
вида∞ − ∞ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем разность к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
( x − ln3 x) = lim x 1 − |
ln3 x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
→+∞x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
Так как при x → +∞ |
, |
ln3 x → +∞ |
, |
то имеем неопределен- |
|
ность |
|
∞ |
|
для дроби |
ln3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3ln2 x |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 ln x |
1 |
|
|
|
lim |
ln |
x |
= lim |
x |
= 3 lim |
ln |
x |
= 3 lim |
x |
= |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
x |
→+∞ |
|
|
→+∞x |
|
|
|
|
|
|
→+∞ x |
|
|
|
x →+∞ |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
= 6 lim |
1 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
= 6 lim |
= 6 lim |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
x |
→+∞x |
|
→+∞ |
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
ln3 x |
|
|
|
|
Тогда |
|
|
lim 1 |
− |
|
|
= 1 |
и, |
следовательно, |
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
x |
|
|
|
|
|
|
ln3 x |
|
|
|
|
|
|
|
|
lim x 1 |
− |
|
|
= +∞ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
x |
|
|
|
|
|
|
|
|
Задача 9.
1
Найти lim x1−x .
x→ 1
Решение
В данном случае имеем неопределенность вида 1∞ .
|
|
1 |
; тогда, логарифмируя, находим ln y = |
|
1 |
|
ln x , |
Пусть y = x |
1−x |
|
|
|
|
|
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim ln y = lim |
ln x |
(неопределенность вида |
0 |
). |
|
|
|
x→ 1 |
→x |
|
1 1 − x |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Применяем правило Лопиталя, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim ln y |
= lim |
= lim |
|
x |
|
= −1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
x→ 1 |
→x 1 1 − x → x 1 |
|
|
|
|
|
|
|
|
Таким образом, окончательно получаем |
|
|
|
|
|
|
|
|
|
|
|
ln lim y = −1, lim y = e−1 |
или |
|
|
|
|
|
|
|
|
|
|
|
x→ 1 |
|
|
|
x→ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
= e−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim x |
1−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти lim |
(tg x)cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь имеет место неопределенность вида ∞ |
0 . |
|
|
|
|
Полагая |
|
y = (tg x)cos x |
и логарифмируя, |
получим |
ln y = |
= cos x ln tg x. Переходим к пределу:
Замечание 2
Следует иметь в виду, что, основываясь только на перемене знака первой производной, нельзя еще заключить о наличии экстремума; необходимо знать еще, что в самой точке функция непрерывна.
Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.
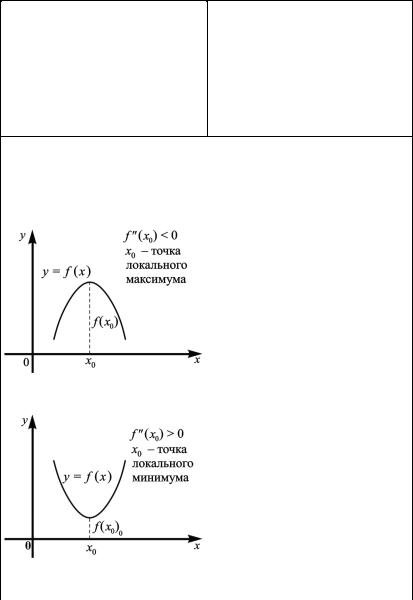
7. |
|
Второе достаточное усло- |
|
вие экстремума функции |
|
|
|
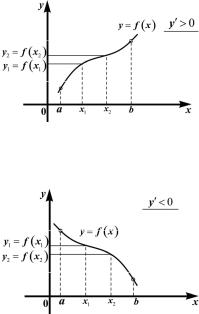
Если в точке x0 первая про- |
|
изводная функции |
f ( x) равна |
|
нулю ( f ′( x0 ) = 0) , а вторая про- |
|
изводная в точке x0 |
существует |
|
и отлична от нуля ( f ′′( x0 ) ≠ |
0) , |
|
то |
при |
f ′′( x0 ) < 0 |
в точке |
x0 |
|
функция |
имеет |
максимум |
Рис. 4.15 |
(рис. 4.15); при f ′′( x0 ) > 0 – ми- |
нимум(рис. 4.16). |
|
|
|
|
|
|
|
Замечание |
|
|
|
|
Если |
f ′( x ) = 0 , а f ′′( x ) = 0 |
|
|
|
0 |
0 |
|
|
или не существует, а также в слу- |
|
чае, когда в точке x0 первой |
|
производной не существует, вто- |
|
рое достаточное условие суще- |
|
ствования экстремума не приме- |
|
нимо и нужно обратиться к пер- |
Рис. 4.16 |
вому условию. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи
Задача 1. Исследовать функцию y = 1 x3 − 2x2 +1 на экс- 3
тремум.
Решение
Данная функция определена и дифференцируема на (−∞ +∞; ) .
Находим y′ = x2 − 4x или y′ = x ( x − 4) .
Определим критические точки по формуле (4.17): y′ = 0 , следовательно, x1 = 0 и x2 = 4 .
x1 = 0 и x2 = 4 – критические точки первого рода.
Применим первое достаточное условие экстремума функ-
ции (п. 6).
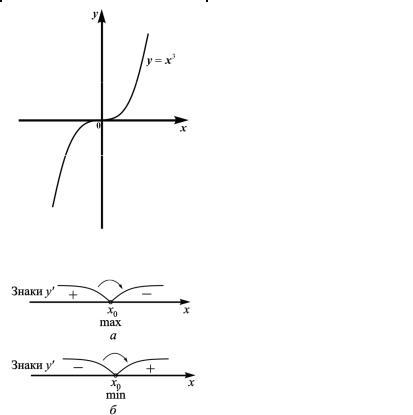
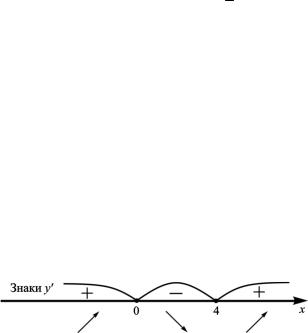
Удобно рисовать следующую схему (рис. 4.17) (стрелками
и обозначим монотонное возрастание и убывание функции на соответствующих интервалах).
Рис. 4.17
Точки x1 = 0 и x2 = 4 разбивают числовую ось −∞ < x< ∞ на три интервала.
Знаки y′ показаны на схеме (см. рис. 4.17) (в этом можно убедиться, взяв, например, по одной точке в каждом из указанных интервалов и подставив соответствующие значения x в y′ ).
Поэтому при x < 0 y′ > 0 , при 0 < x < 4 y′ < 0 , а при x > 4 y′ > 0 . Следовательно,
– на (−∞ ;0) |
функция возрастает, ( ) |
– на (0; 4) |
убывает, ( ) |
– на (4; +∞ |
) |
возрастает. ( ) |