
книги / Математика введение в анализ, дифференциальное исчисление функции одной переменной
..pdf
y = cos x , y = tg x , y = ctg x
являются периодическими. Для первых двух из них период равен 2π, а две последние имеют период π .
Следует запомнить:
функции sin ωx и cos ωx имеют
период T = |
2π |
(ω≠ |
0) , а функ- |
||||
ω |
|||||||
|
|
|
|
|
|
||
ции tg ωx |
и ctg ωx |
имеют пери- |
|||||
од T = |
π |
|
(ω≠ |
0) . |
|
||
ω |
|
||||||
|
|
|
|
|
|||
Замечание 2 |
|
||||||
Следует иметь в виду, что |
|||||||
далеко не всякая функция является периодической.
Примеры непериодических функций: y = x3 , y = arcctg x ,
y = ex , y = lg x .
Задачи
Задача 1. Установить чётность или нечётность функций:
а) f (x) = x3 cos 5x ;
б) f (x) = 1 (5x + 5− x ) ; 2
в) f (x) = x4 − 4x3 +1 ; |
|
|
||
г) f (x) = lg |
2 + x |
. |
|
|
|
|
|
||
|
2 − x |
|
|
|
Решение |
−( ∞ +∞; |
) , поэтому оче- |
||
а) Область определения функции: x |
||||
видно, что если x −( ∞ +∞; ) , то и (−x) |
−( ∞ +∞; |
) . Заменяя x на |
||
(−x) , получим |
|
|
||
f (−x) = (−x)3 cos 5(−x) = − x3 cos 5x = − f (x) .
21
Следовательно, данная функция нечётная (формула 1.6).
б) Областьопределения функции x −( ∞ +∞; |
) . Вэтомслучае |
|||
f (−x) = |
1 |
(5− x + 5x ) = f (x) , |
|
|
|
|
|||
2 |
|
|
|
|
т.е. исследуемая функция является чётной (формула 1.5). |
||||
в) Область определения функции x −( ∞ +∞; ) . |
Заменяя x |
|||
на (−x) , получим |
|
|
||
f (−x) = (−x)4 − 4(− x)3 + 1 = x4 + 4x3 + 1. |
|
|||
Таким образом, здесь f (−x) ≠ f (x) и |
f (−x) ≠ − |
f (x) . По- |
||
этому данная функция чётной или нечётной не является.
г) Область определения функции: x −( 2; 2) – интервал, симметричный относительно точки 0, поэтому для любого значения x из области определения функции значение (−x) также принадлежит области определения этой функции.
Находим:
|
2 − x |
|
2 + x −1 |
||
f (−x) = lg |
|
|
= lg |
|
|
|
+ x |
|
|||
2 |
|
2 − x |
|||
|
2 + x |
|
|
= − lg |
|
|
= − f (x) . |
|
|||
|
2 − x |
|
|
Следовательно, данная функция является нечётной.
Задача 2. Найти основной (наименьший) период функций:
а) |
f (x) = cos8x ; |
|
|
|
|
|
|
|
||||
б) |
f (x) = sin |
x |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|
|
|
|
||
в) f (x) = tg 5x . |
|
|
|
|
|
|
|
|||||
Решение |
|
|
|
|
|
|
|
|||||
а) |
Поскольку основной период функции cos x |
равен 2π, то |
||||||||||
основной период функции |
f (x) = cos8x равен |
T = |
2π |
, |
где |
|||||||
ω |
||||||||||||
|
|
|
|
2π |
|
π |
|
|
|
|
||
ω= 8 , следовательно, T = |
= |
. |
|
|
|
|
||||||
|
|
|
|
|
|
|||||||
|
8 |
4 |
|
|
|
|
|
|||||
22
б) Для функции sin x основной период равен 2π, поэто-
му основной период функции |
f (x) = sin |
x |
равен |
2π |
= 8π , |
||||
|
4 |
|
|
|
1 |
|
|||
т.е. T = 8π. |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
в) Основной период функции tg x равен π , поэтому основ- |
|||||||||
ной период функции f (x) = tg 5x |
равен |
π |
, т.е. T = |
π |
. |
|
|
||
|
5 |
|
|
5 |
|
|
|
||
Задача 3. Проверить, будет ли функция ограниченной или неограниченной:
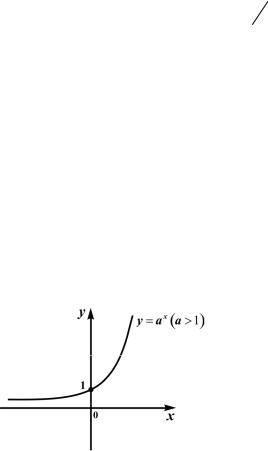
а) y = a x (a > 1) ;
б) y = −x2 ; в) y = sin x ; г) y = tg x .
Решение
а) Функция y = ax будет ограниченной снизу, так как ax > 0 для любого x (рис. 1.14). Согласно формуле (1.11) m = 0.
Рис. 1.14 |
|
Функция сверху не ограничена, |
следовательно, функция |
y = ax неограниченная для x (–∞ ; +∞ |
); |
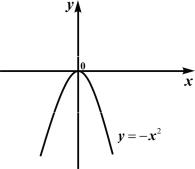
б) Функция y = –x2 будет ограниченной сверху (рис. 1.15). Согласно формуле (1.12) f (x) ≤ 0, т.е. M = 0.
23
|
|
|
|
Рис. 1.15 |
|
|
|
|
|
Функция снизу не ограничена, |
следовательно, функция |
||||||||
y = –x2 неограниченная для x (–∞ ; +∞ |
); |
|
|
|
|
||||
в) y = sin x – ограниченная функция, так как она ограничена |
|||||||||
и сверху, и снизу, т.е. |
|
|
|
|
|
||||
−1 ≤ sin x≤ 1 или |
|
sin x |
|
≤ 1, x (–∞ |
; +∞ |
). |
|
|
|
|
|
|
|
||||||
Согласно формуле (1.13) M = 1; |
|
|
|
π |
|||||
|
|
|
|
|
π |
||||
г) Функция y = tg x на интервале |
− |
|
; |
|
будет неограни- |
||||
|
|
||||||||
|
|
|
|
|
|
2 |
|
2 |
|
ченной, так как на этом интервале она не ограничена сверху и не ограничена снизу (§3, рис. 1.29).
§ 3. Обратная функция. Сложная функция. Основные элементарные функции и их графики
Основные формулы |
Определения |
||
ирисунки |
|
изамечания |
|
1. Обозначение |
функции |
Пусть функция y = f (x), оп- |
|
обратной к функции y = f (x): |
ределенная на множестве D, |
||
x = ϕ (y) |
(1.15) |
непрерывна и |
монотонна и |
имеет область значений E. Если |
|||
|
|
для каждого y |
E существует |
|
|
единственное значение x такое, |
|
|
|
что f (x) = y, то это соответствие |
|
24 |
|
|
|
|
определяет некоторую функцию |
||||
|
x от аргумента y, т.е. x = ϕ (y), |
||||
|
называемую обратной по от- |
||||
|
ношению |
к данной функции |
|||
|
y = f (x). |
|
|
|
|
|
Следует запомнить: |
|
|||
|
достаточным условием сущест- |
||||
|
вования обратной функции яв- |
||||
|
ляется |
строгая |
монотонность |
||
|
функции y = f (x). При этом ес- |
||||
|
ли функция возрастает (убыва- |
||||
|
ет), то и обратная функция воз- |
||||
|
растает (убывает). |
|
|||
|
Замечание 1 |
|
|||
|
Функция y = f (x) и обрат- |
||||
|
ная к ней x = ϕ (y) изображаются |
||||
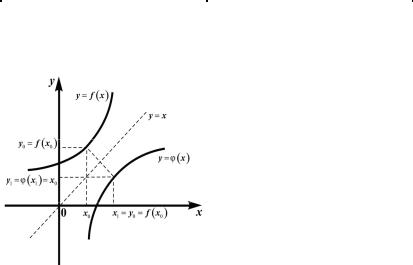
Рис. 1.16 |
одной и той же кривой, т.е. |
||||
|
графики их совпадают. |
|
|||
|
Но, как обычно, для обрат- |
||||
|
ной функции аргумент обозна- |
||||
|
чают через x, а значение функ- |
||||
|
ции – через y, т.е. записывают |
||||
|
ее в виде y = ϕ (x). |
|
|||
|
Графики функций y = f (x) |
||||
|
и y = ϕ (x) симметричны относи- |
||||
|
тельно прямой y = x (рис. 1.16). |
||||
|
Замечание 2 |
|
|||
|
Функции y = f (x) и y = ϕ (x) – |
||||
|
взаимно обратные функции. |
|
|||
2. Если y = f (u), где u = ϕ (x), |
Если функция y = f (u) |
оп- |
|||
то |
ределена |
на |
множестве |
D, |
|
y = f [ϕ (x)] – (1.16) |
а функция u = ϕ (x) определена |
||||
на множестве D1, причем |
|||||
сложная функция или функция |
x D1 |
|
соответствующее зна- |
||
от функции. |
чение |
u = ϕ (x) D, тогда |
на |
||
|
множестве D1 определена функ- |
||||
25
ция y = f [ϕ (x)], которая называется сложной функцией от x.
Замечание 1
Переменная u называется
промежуточным аргументом
сложной функции.
Замечание 2
Сложная функция может иметь несколько промежуточных аргументов.
Замечание 3
Термин «сложная функция» указывает только на характерную особенность в аналитической конструкции функции и отнюдь не означает какой-то особой ее сложности в обычном понимании этого слова.
3. Основныеэлементарные функции
а) Степенная функция |
n |
– |
действительное число |
|
|
|
|||
y = xn |
(1.17) |
(n R) |
|
|
|
|
Частные случаи |
||
|
|
1) n – целое положительное |
||
|
|
число. |
|
|
|
|
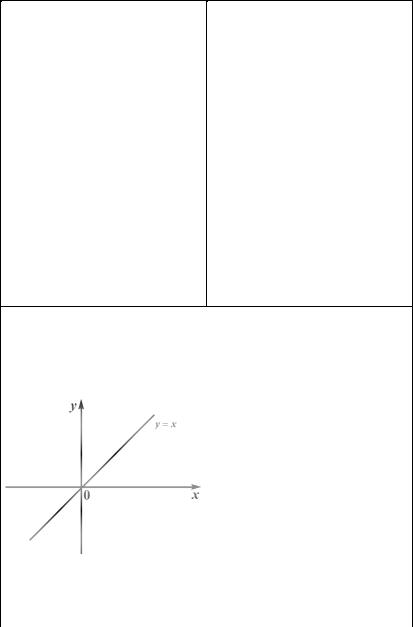
n = 1: y = x. |
||
|
|
График – прямая линия, ко- |
||
|
|
торая |
является биссектрисой |
|
|
|
первого и третьего координат- |
||
|
|
ных углов (рис. 1.17). |
||
|
|
n = 2: y = x2. |
||
Рис. 1.17 |
|
Графиком является парабо- |
||
|
|
ла, ветви которой направлены |
||
|
|
вверх, |
а |
вершина находится |
|
|
в точке с координатами (0;0). |
||
26
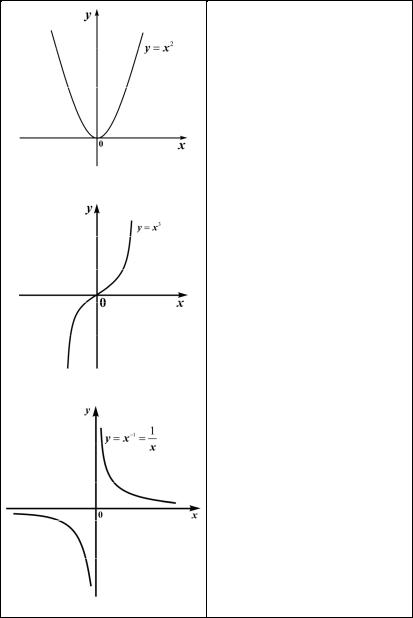
График симметричен относительно оси OY (функция чёт-
ная) (рис. 1.18).
Рис. 1.18
n = 3: y = x3.
Графиком является кубическая парабола, расположенная в первом и третьем координатных углах. График симметричен относительно начала координат (функция нечётная) (рис. 1.19).
Рис. 1.19
2) n – целое отрицательное |
||||
число. |
|
|
|
|
n = –1: y = |
1 |
. |
|
|
|
|
|||
|
|
x |
|
|
Графиком является |
гипер- |
|||
бола, расположенная в первом и |
||||
третьем |
координатных |
углах. |
||
График |
симметричен |
относи- |
||
тельно начала координат (функ- |
||||
ция нечётная). |
|
|||
Рис. 1.20 |
|
|
|
|
27

Рис. 1.21
Рис. 1.22
Функция y = 1 . определе- x
на при всех значениях x, кроме x = 0 (рис. 1.20).
n = –2: y = 1 . x2
Графиком является гипербола, расположенная в первом и втором координатных углах. График симметричен относительно оси OY (функция чётная).
Функция y = 1 . опреде- x2
лена при всех значениях x, кро-
ме x = 0 (рис. 1.21).
3) n – дробно-рациональное число.
n = |
1 |
: y = x. |
|
||
2 |
|
|
График – ветвь параболы, которая расположена в первом координатном углу.
Область определения функ-
ции: x [0;+∞ ) .
Область значений функ-
ции: y [0;+∞ ) (рис. 1.22).
28
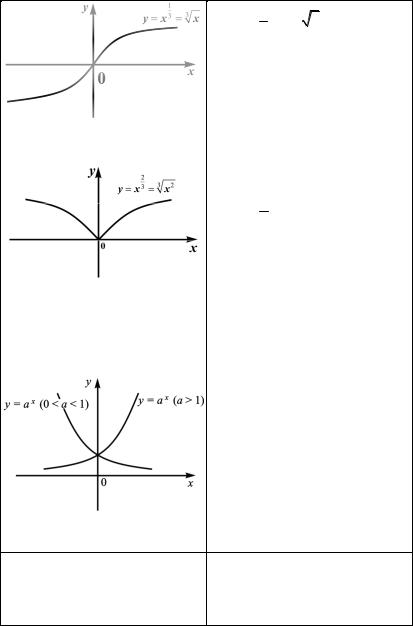
n = 1 : y = 3 x. 3
График – кубическая парабола, расположенная в первом и третьем координатных углах
(рис. 1.23).
Рис. 1.23
n = 2 : y = x2/3 (рис. 1.24). 3
Рис. 1.24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Показательнаяфункция |
|
|
|
|
|
|
y = ax |
(1.18) |
a > 0; |
а ≠ |
1. |
|
|
|
|
Функция |
y = ax |
определена |
||
|
|
при всех значениях x. Область |
||||
|
|
значений |
функции: |
y (0;+∞ ) |
||
|
|
(рис. 1.25). |
|
|
|
|
|
|
Замечание |
|
|
||
|
|
Если a = е, то показа- |
||||
|
|
тельную |
функцию |
называют |
||
Рис. 1.25 |
|
экспонентой |
|
и обозначают |
||
|
y = ex = exp(x) |
. |
|
|||
|
|
|
|
|
|
|
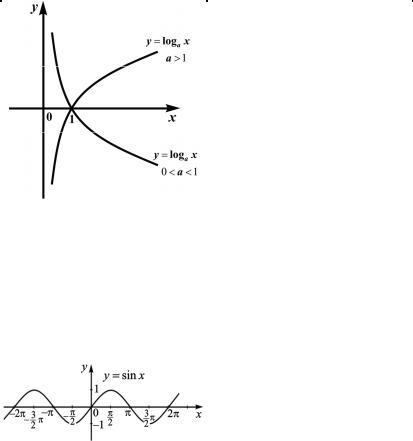
в) Логарифмическая
функция
y = loga x |
(1.19) |
a > 0; а ≠ 1. |
29
|
|
|
Логарифмическая |
функ- |
|
|
|
|
ция определена при x > 0. |
||
|
|
|
Область |
значений функции: |
|
|
|
|
y ( –∞ +∞; |
) (рис. 1.26). |
|
|
|
|
Функция y = loga x |
обрат- |
|
|
|
|
ная для функции y = ax . |
|
|
|
|
|
Замечание |
|
|
|
|
|
ln x – натуральный логарифм |
||
|
|
|
(ln x = loge x) . |
|
|
|
|
|
lg x – десятичный логарифм |
||
Рис. 1.26 |
|
(lg x = log10 x) . |
|
||
|
|
|
|
||
|
|
|
|
||
г) Тригонометрические |
|
|
|
||
функции: |
|
|
|
|
|
y = sin x , |
y = cos x , |
|
Функция y = sin x. |
|
|
y = tg x , |
y = ctg x |
(1.20) |
Область определения – все |
||
действительные числа. |
|
||||
|
|
|
Область значений – отре- |
||
|
|
|
зок [–1;1], т.е. функция огра- |
||
|
|
|
ниченная. |
|
|
|
|
|
Функция y = sin x периоди- |
||
|
|
|
ческая (T = 2π ). |
|
|
|
|
|
Функция нечётная, т.е. |
||
Рис. 1.27 |
|
sin(–x) = –sin(x) (график |
сим- |
||
|
|
|
метричен относительно нача- |
||
|
|
|
ла координат). |
|
|
|
|
|
Замечание |
|
|
|
|
|
График функции y = sin x |
||
|
|
|
(рис. 1.27) называется сину- |
||
|
|
|
соидой. |
|
|
|
|
|
Функция y = cos x. |
|
|
|
|
|
Область определения – все |
||
|
|
|
действительные числа. |
|
|
30
